灾损曲线的构建及其在巨灾保险中的应用

张涵博

巨灾保险是巨灾风险管理中的重要工具。通过巨灾保险，可以将自然灾害的损失风险进行有效的分散和转移，促进防灾减灾和灾后重建工作的开展，对于一国的经济社会繁荣稳定有着非常重要的作用。我国是一个自然灾害频发的国家，面临着除了火山爆发之外所有的巨灾风险，巨灾保险对我国有着尤为重要的意义。

巨灾风险有着与常规风险截然不同的特点:从发生频率来看，常规风险通常发生频率较高，但巨灾风险的发生频率极低;从损失规模来看，常规风险的损失一般只与单个风险标的的价值有关，而在巨灾风险中通常某一地区的所有风险标的都受影响;从空间和时间分布来看，常规风险的发生和分布比较分散，但巨灾风险通常会在某一时间、某一地区集中发生，造成高额损失。上述特点使得巨灾保险相对于普通保险在产品开发和定价方面有着更大的困难:常规风险的频发性使得采用大数定律等传统保险精算方法估计风险损失的波动性较小，而巨灾风险的低频高危性使得传统方法对风险损失的估计与实际情况可能会有较大出入。要衡量巨灾风险的大小，必须通过巨灾建模(Catastrophe Modeling)，在经验数据的基础上构建巨灾损失模型。

灾损曲线是反映巨灾的损失程度与发生频率之间关系的曲线，是巨灾损失模型的核心组成部分。它可以确定某一损失规模巨灾事件的发生频率，从而求出巨灾总损失的数学期望值并实现巨灾保险的定价。超概率曲线(Exceedance Probability Curve，EP)是灾损曲线的主要形式之一。本文将首先介绍超概率曲线构建的一般原理，进而提出一种在经验数据的基础上通过计算机模拟构建巨灾超概率曲线的方法，最后将探究超概率曲线在巨灾保险中的应用及意义。

一、构建超概率曲线的一般原理

超概率曲线是概率论中进行累积频率分析(Cumulative Frequency Analysis)的重要工具，它是用图形表示在给定时期内或给定事件中超过一定损失水平事件的发生概率，通常用纵轴表示概率，横轴表示损失水平。对于某种灾害损失，超概率是指在某段时间内或某些灾害事件中，发生大于特定损失规模灾害事件的概率。当损失为0时，超过这一损失的概率为1;随着损失规模的提高，超概率将随之下降。

一般而言，在构建超概率曲线时，服从以下一些基本假设:

1.有一系列自然灾害损失事件Ei;

2.对于每起事件，都有发生概率pi和对应的损失Li;

3.某一年中灾害发生的次数并不局限于一次，可以是多次;

4.所有灾害事件都是相互独立的，服从 Bernoulli分布，即对于任意的m和n，都有P(Em/En)=P(Em)，每起灾害损失事件的发生时间、发生频率、损失程度等参数都不受其他灾害损失事件发生与否的影响。

在以上假设下，每一起灾害损失事件Ei都是一个独立随机变量，其概率分布函数定义如下。

P(Ei发生)=pi

P(Ei不发生)=(1－pi)

若灾害不发生，则损失为零。所以某年中某一灾害事件Ei的期望损失为:

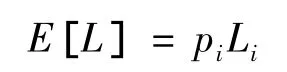
如果我们用AAL(Average Annual Loss)来表示所有灾害事件在一年中的总期望损失，则其表达式为:

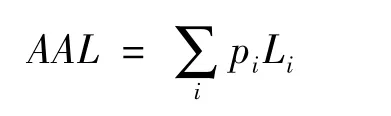
假设某一年中只发生了一次灾害事件，则某一损失水平的超概率EP(Li)，即超过该损失水平的灾害损失事件的发生概率，就相当于1减去这一年中所有低于该损失水平的灾害事件都没有发生的概率。它可以由以下式子求得:

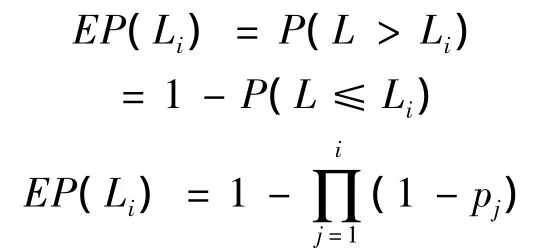
将相应的损失额度Li和相应的EP(Li)绘制在图上，即可得到这一年中巨灾损失的超概率曲线，如下图:

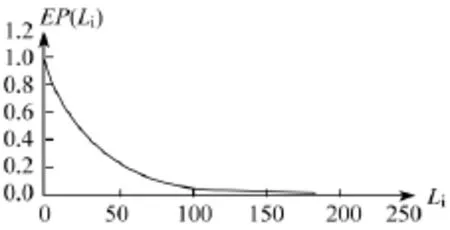
图:超概率曲线示例图

在图中，横轴Li表示损失水平(横轴上的数字是假设的损失值)，纵轴EP(Li)表示其所对应的超概率。在损失水平为0时，所有损失事件的损失额度都会超过0，此时对应的超概率是1。一般而言，随着损失水平的提高，相应的超概率也越来越低，但其下降幅度将逐步减缓。即超概率曲线满足以下性质:

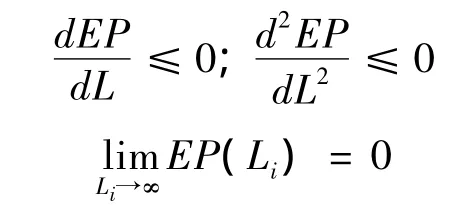
二、通过计算机模拟构建年度巨灾损失超概率曲线

在以上基本原理中，若要构建年度灾害损失超概率曲线并求得AAL，必须能够确定在某一年中，某一特定的灾害损失事件Ei发生的确切概率 pi。理论上，pi可以通过统计多年的经验数据获得。但在实际中，一方面，由于我国巨灾监控体系是在建国之后才逐步建立和完善的，历史数据并不全面;另一方面，改革开放后经济社会快速发展使得经济体制转型前后的灾害损失数据缺乏可比性，因此中国巨灾损失历史数据非常有限，通过简单统计这些数据得到的pi并不准确。在构建超概率曲线时应当借助计算机生成虚拟的灾害事件来模拟灾害的损失情况，以弥补历史数据的不足。本部分将提出一种在经验数据的基础上通过计算机模拟构建年度巨灾损失超概率曲线的方法。首先根据历史数据得到单起灾害事件中损失的分布情况，然后建立每年某种巨灾事件发生次数的分布，最后由计算机模拟年度灾害损失情况以构建年度巨灾损失超概率曲线。

第一步:建立单起灾害事件损失分布

一般而言，对于地震、台风这样的自然灾害，我国每年都会发生数十次，在二十年的时间里能够积累到数百个有效的灾害损失数据。如果这些灾害事件的损失都服从同样的分布，数百起事件已经足以构成大样本，通过统计这些数据就能找到单起灾害事件的损失分布。在第一步中，我们把某种自然灾害的总体看成一个随机变量，把所收集的该种灾害损失事件看作是巨灾损失总体的样本。在构建单起灾害事件损失分布时接受以下假设:

1.收集的每起该种灾害损失事件Ei都是该种灾害损失随机变量ξ的一个样本，且样本容量足够大;

2.所有灾害损失事件Ei都服从同样的分布;

3.所有灾害损失事件Ei都是相互独立的;

4.在每一起灾害损失事件中，对于某一可能的损失水平Li，有对应的损失概率pi。

在以上假设下，某一时间段内我国所有的该种灾害损失事件相当于在同样条件下重复进行的数百次实验，构成了一个独立试验序列概型。由于每次试验的结果Ei与其他各次试验结果无关，因此这一系列重复实验构成了n重Bernoulli实验。

由于假设所有灾害损失是一个随机变量总体ξ，可以设(x1，x2，…xn，)是总体 ξ的样本 Ei的观察值，即每起灾害损失事件中的经济损失数额。将它们按大小排列为，令

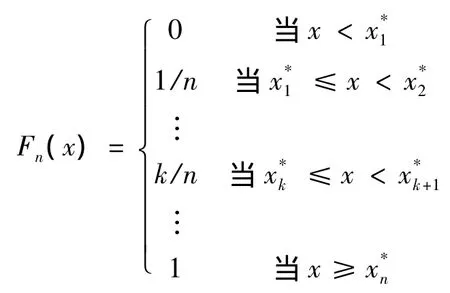
则Fn(x)的图形就构成了累积频率曲线。它是跳跃式上升的一条阶梯曲线。若观测值不重复，则每一跃度为1/n;若观测值有重复，则按照1/n的倍数跳跃上升。

根据Bernoulli大数定律，在独立试验序列中，当试验次数n无限增加时，事件A的频率k/n(k是n次试验中事件A发生的次数)，收敛于它的概率P(A)=p。即，对于任意给定的ε＞0，有

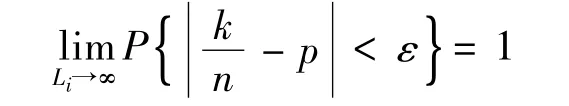
也就是说，当试验在不变的条件下重复进行很多次时，随机事件的频率在它的概率附近摆动，并将随着实验次数的增加而不断趋近其概率。在样本的累积频率曲线Fn(x)中，对于任何实数x，Fn(x)等于样本的n个观察值中不超过x的个数除以样本容量n，因此Fn(x)可以作为未知的整体ξ的分布函数Fξ(x)的一个近似。样本容量n越大，近似得越好。在数百起灾害损失事件的大样本下，可以近似地认为样本累积频率曲线Fn(x)等同于灾害损失整体分布曲线Fξ(x)。由于Fn(x)实质上是所有低于某一损失水平x的灾害事件发生的概率，因此用1－Fn(x)可得出所有高于x的灾害损失事件的发生概率，即单起灾害损失的超概率曲线。

需要说明的是，并不是所有的灾害损失数据都能够符合前提假设:

第一，对于最重要的“同分布”假设，灾害损失的原始数据很可能无法满足:随着经济社会的发展，一个地区的财富积累会越来越多。在其他条件不变的情况下，同样破坏程度的灾害事件造成的损失将逐步扩大。再加上通货膨胀因素，严格来说，在长时间跨度中，灾害损失并不符合同分布假设。在这种情况下应对损失数据进行一定的处理，以消除通货膨胀或经济增长等外部因素的影响。

第二，自然灾害的特点可能使得“独立”这一假设在现实中不一定成立。同一类型的不同灾害事件之间，以及不同类型的不同灾害事件之间，的确可能存在一定的因果关系，并不一定是完全独立的。由于科学界对自然灾害的形成和相互作用机理仍未充分研究，因此只能暂时假定所有灾害事件都是相互独立的。

第三，某些自然灾害的发生频率较低，难以满足“样本容量足够大”的假设。在我国，海啸、火山爆发发生的可能性微乎其微，由于样本容量太小，无法通过上述方法来找出这两种自然灾害的损失分布情况。

此外，对于一些极端损失事件，在必要时应当作为极端值舍弃。如汶川地震，其损失占2008年当年地震直接经济损失的99.16%，占 1990～2008年中国地震总损失的90%以上，远超出其他地震的损失规模(郑通彦，2009)。极端大的损失对应着非常小的概率，为了维持数据的可处理性，根据小概率事件的实际不可能性原理，在构建地震的单起灾害损失分布时应当去除汶川地震这样的极端事件。

经过以上数据处理后可建立单起灾害事件损失分布模型。通过它可以得到在每起灾害事件中，损失水平超过Li的概率EP(Li)，由此构建单起灾害损失事件超概率曲线。

第二步:构建年度灾害发生次数分布模型

与构建单起灾害损失分布模型的假设类似，我们假定每年某种灾害的发生次数也是相互独立并服从同一分布的。一般而言，每年某种自然灾害(如地震、台风、洪水等)的发生次数往往呈现出围绕着平均值上下波动的现象。如果有相当长的年度灾害发生次数数据(如20年左右)，可以验证其是否服从正态分布。

首先，绘出年度灾害发生次数数据的分布直方图，并求出其峰度与偏度。如果直方图呈现出正态分布的形态，并且这些数据的峰度和偏度趋近正态分布的特征(峰度为3，偏度为0)，则可以近似地认为年度灾害发生次数数据基本符合正态分布。

为了进一步检验样本数据是否服从正态分布，可以通过统计软件来进行相关检验:通过Eviews软件可以求出样本数据的Jarque－Bera统计量，通过 SAS或SPSS软件也可以求出样本数据的Shapiro－Wilk或Kolmogorov－Smirnov统计量。如果统计量的值大于0.05，则接受检验原假设，即样本数据服从正态分布。

若样本数据的期望为μ，标准差为σ，样本数据具有较大的样本容量，符合正态分布的特征，且能够通过正态分布的相关检验，则可近似地认为年度灾害发生次数分布服从期望为μ、标准差为σ的正态分布。

第三步:通过计算机模拟构建年度灾害损失超概率曲线

在前面两步中，我们分别建立了单起灾害损失分布和年度灾害发生次数分布。接下来，通过计算机随机抽取每年灾害发生次数和每次灾害损失，经过大量的抽取模拟后(如1000年)，可以得到长时间段的年度灾害损失状况，以此可构建年度灾害损失分布曲线。

在构建某种年度灾害损失超概率曲线时，我们假设:1.任意一起灾害的损失都服从第一步中得到的单起灾害事件损失分布;2.任意一年中某种灾害发生次数都服从第二步中得到的年度灾害发生次数分布，即期望为μ、标准差为σ的正态分布。

在以上假设下，采用以下算法模拟某种灾害年度损失总额:

步骤一，根据年度灾害发生次数分布生成第i年灾害发生次数ni;

步骤二，根据单起灾害事件损失分布生成ni次灾害损失事件，每次分别有kij的损失，构成第i年中的灾害损失序列;

步骤三，将这ni次灾害事件的损失加总，构成第i年的灾害损失总额

步骤四，将步骤一至步骤三重复m次，得到m年中每年的年度灾害损失总额序列:K1，K2，…，Ki…，Km－1，Km。

最后，采用第一步中的方法，使用这m个模拟的年度灾害损失总额构建它们的分布模型，就得到了年度灾害损失超概率曲线。在计算机的辅助下可以模拟出数千年的年度灾害损失情况，由此得到的超概率曲线比简单通过几十年的灾害损失记录得到的超概率曲线更加准确。

三、灾损曲线在巨灾保险中的应用

以超概率曲线为代表的灾损曲线确立了灾害损失的大小与发生概率之间的关系，是巨灾保险费率厘定、风险评估、承保决策及风险转移过程中必不可少的重要工具。在前文构建的超概率曲线的基础上，本部分将探究灾损曲线在巨灾保险中的应用。

第一，灾损曲线为巨灾保险的费率厘定提供了依据。在厘定保险的纯保费时，需要满足的基本条件是收取保费的现值应等同于损失赔付期望的现值。由于灾害事件发生频率低，通过历史经验数据很难准确估计出未来损失的期望。以美国1994年北岭地震为例，在地震前美国地震保险的低费率(每千美元保额的保费约为2美元)导致北岭地震造成的125亿美元巨额保险索赔，超过了此前20年间美国保险公司所收取的地震保险保费总和(朱文杰，2006)，因此合理的费率对巨灾保险至关重要。在建立合适的灾损曲线后，保险公司能够掌握灾害损失大小与发生概率之间的关系，通过计算出年度总期望损失(AAL)而得到的巨灾保险费率将更加符合实际情况。

第二，灾损曲线使保险公司能够较准确地评估其所承保的巨灾风险的规模。保险公司对于灾害赔付的承受能力是有一定限度的，为了确保公司经营的稳定性和连续性，对承保风险的评估非常必要。根据超概率曲线可以得到一定损失规模灾害事件的重现周期，从而评估巨灾风险的大小。在超概率曲线示例图中，损失为100的灾害事件对应的超概率约为0.052，这意味着损失规模超过100的灾害事件的重现周期是1÷0.052≈19.2 年。如果一家保险公司设定其所能接受的最大风险是重现期为50年的灾害事件，即 EP=0.02，那么根据超概率曲线示例图，在该巨灾保险中最大可能损失约为132。

第三，灾损曲线可以为保险公司巨灾保险的承保决策提供依据。为了确保安全稳健经营，保险公司会尽量避免出现偿付能力不足的情况。假如一家保险公司可以接受偿付能力不足情况的最大出现概率是p0，用L代表赔付损失，n代表承保保单的数量，a代表每份保单收取的保费，S代表现有盈余，那么保险公司经营的约束条件是:

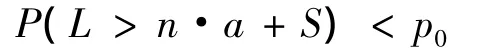
在超概率曲线中，根据EP=p0可以求出对应的L。若保险公司的保费收入与盈余之和无法达到L，那么此时就无法满足以上约束条件，继续承保该巨灾保险会使公司面临偿付能力不足的风险。

第四，灾损曲线可用于巨灾风险转移决策。巨灾风险具有发生频率低、损失规模大、较易集中发生的特点，单一一家保险公司往往无法单独承受巨灾保险的巨额赔付。承保巨灾保险的保险人可选择再保险或巨灾债券等风险转移措施，以进一步分散巨灾风险并减少需要持有的自有资本，但需支付再保费或债券利息而降低保险公司的预期收益。为了在保证偿付能力的前提下实现收益最大化，保险公司必须维持自留风险和分出风险的平衡。在评估巨灾风险转移措施时，灾损曲线具有以下作用:一方面，通过灾损曲线，原保险人和再保险人可以计算自留风险和分出风险的期望赔付，进而确定再保险的保费或巨灾债券的利息;另一方面，保险人可以通过灾损曲线计算出在满足偿付能力约束条件时自身所能承受的最大风险，进而决定分出额的大小。因此，灾损曲线可以帮助保险公司做出合适的巨灾风险转移决策。

总体而言，灾损曲线作为巨灾模型的核心组成部分，是评估巨灾风险规模的重要工具，对巨灾保险的产品开发、运营管理有着决定性的作用。应用计算机模拟使得灾损曲线能够摆脱历史数据不足带来的困扰，增强了灾损曲线的准确性，并使得巨灾保险的定价和保险公司的决策更加合理。