SPC在实验设备质量控制中的应用

陈 宏， 陈国柱

(浙江大学电气工程学院，浙江杭州310027)

0 引言

工科高校实验教学中很重要的一部分实验任务是测量，然而，由于实验设备的性能或者测量环节中的其他可控或者不可控的因素的影响，造成实验中测量精度不高，实验误差偏大的状况，甚至于产生故障，无法完成实验任务［1-4］，因此实验设备良好的工作质量，在实验中显得非常重要。传统的质量检验手段是定期计量或者事后检查，这种检验滞后的方式，严重影响现场的实验质量。

在教学实践中，实验设备的质量状况表现在测量的数据中，虽然实验设备测量的数据本身并没有提供质量信息，但是数据经过统计方法整理和分析，就成为科学评价实验教学设备质量水平的依据［5］。在使用实验设备的测量过程中，测量人员、实验设备、测试流程、操作规范和测量环境构成一个测量系统［6］。在工程应用领域中，通常从质量管理的角度出发，采用科学统计方法对测量系统实现质量控制。统计过程控制(Statistic Process Control，SPC)就是一种过程控制技术，对过程控制中的质量特性分析和监控，为达到持续质量改进提供了科学的方法［7］。SPC对实践过程中的异常波动进行实时监控，对潜在的异常趋势提出预警，以便管理人员及时采取措施，消除异常，恢复稳定，从而达到控制和提高质量的目的，成为工业生产中降低维修率、保证质量的稳定性和提高生产效率的有力的技术支持［8-11］。在分析SPC和实验室设备的质量控制后，发现SPC在实验室设备的质量控制中也存在实际运用的可操作性。

1 统计过程控制

1924年5月美国Shewhart博士绘制了第一张控制图并开创了SPC的研究领域，SPC目的就是要建立并保持生产过程处于可接受的、稳定的质量水平，以确保产品符合客户的质量要求。如果质量水平原来处于稳定状态，SPC帮助发现异常状况，利于去除影响因素，使过程回复历史水平;如果质量水平原来就不稳定，SPC帮助找出异常点，去除影响因素，使生产过程回到受控状态。

1．1 SPC 的原理

传统的质量检验是事后的质量保证，会导致检验滞后，造成经济损失，Shewhart的控制图能够在线衡量质量水平并进行现场过程控制。SPC采用的统计工具是控制图，在控制图中按照时间顺序取值描点，记录过程参数的测量值。通过对控制参数的实时统计分析，计算控制界限，绘制中心线(Center Line，CL)、上控制界限(Upper Control Line，UCL)和下控制界限(Lower Control Line，LCL)，观察控制图，分析参数是否受控。其中CL、UCL和LCL不是被测参数的技术指标，而是根据数据分析计算得到的控制界限。

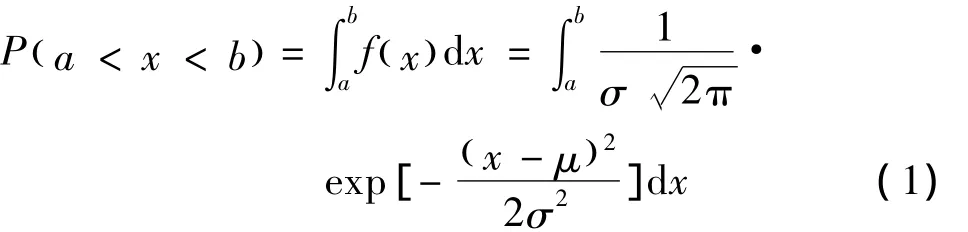
通过对正态分布密度函数的积分计算，可以得到不同质量特性值区间的概率，式中:μ为均值，σ为标准偏差。Shewhart认为对100%的质量数据实施质量控制是不可能实现的，在μ±3σ范围内包含全部质量数据的99．73%，对99．73%的质量数据实施控制，生产过程就基本上处于受控状态［12］。Shewhart将过程处于稳定受控状态时质量数据的典型分布的正态分布曲线作为控制区间设计了控制图，如图1所示。

图1 控制图的原理图

图中的分布曲线被划为对称的A、B、C共6个区，每个区的高度为σ。高斯分布的±σ范围划为C区;高斯分布的±σ～±2σ之间划为B区;高斯分布的±2σ～±3σ之间划为A区。当样本是质量受控的，样本测量值在99%以上的时间里分布在LCL至UCL的范围内，即A区以内;如果有一个点在控制范围之外，就说明设备、数据采集方式或者测量过程发生了变化，必须采取纠正措施。

SPC采用控制图作过程分析，根据控制图的原理，SPC研究的是单一变异来源、正态、独立分布的统计过程。首先数据只有单一变异来源，不能直接对多变异来源的数据作控制图，多变异来源的数据采用其他统计方法作质量分析;其次数据必须是正态分布的;最后测量数据必须具有独立性，如果呈现自相关或者线性趋势，就不能直接作控制图，对于正相关的数据需要运用指数加权移动平均(Exponentially Weighted Moving Average，EWMA)模型对测量结果的微小变异作控制图，并预测未来的测量结果;对于线性变化的数据也不能直接作控制图，需要采用其他统计方法作质量分析。

1．2 SPC的判断准则

为了衡量测量过程是否达到需求，统计学上通常使用假设检验推断在接受某个结论的同时，产生错误的概率会有多少［13］。假设检验是依据一定的概率原则，估计数值与总体数值是否存在显著差异，以较小的出错风险来判断是否应当接受原假设选择的一种检验方法。设定显著检验水平α=0．05，假设检验的条件如式2:

式中:H0是原假设;HA是备择假设;μ是测量数据的均值。若实验结果的偏差分析显著性检验水平的可能性p＞α，不拒绝原假设H0，即接受原假设，认为均值等于目标值;同理，若实验结果的偏差分析显著性水平的可能性p＜α，表明至少有一个均值显著大于目标值，拒绝原假设H0，即接受备择假设HA，则均值大于目标值。

当实验结果的偏差分析显著性水平的可能性p＞α，则原假设是正确的而被拒绝，会发生第一类假设检验错误;当实验结果的显著性水平的可能性小于α，则原假设是错误的而没有被拒绝，会发生第二类假设检验错误。两种情况的概率:

在工业生产的质量控制过程中，第一类假设检验错误发生时导致可接受的产品被拒绝，即“合格”的产品被判定“不合格”;第二类假设检验错误发生时导致因接受了“不合格”的产品使用户承担风险［13］。在测量系统的过程控制能力分析时，第二类假设检验的错误会导致不合格产品流入市场，造成生产厂家的重大损失;而第一类假设检验的错误不会影响市场中的产品质量，是可以接受的。因此SPC采用第一类假设检验作为衡量实验设备测试指标的前期判断。

SPC关注生产流程、测量过程或者设备运行的关键特性，统计过程的数据分布的标准偏差越小，输出结果与工作指标越接近，因此SPC的衡量指标是过程的稳定性和过程的能力。

1．2．1 稳定性

统计过程的稳定性用数据样本均值来衡量，随时间变化均值保持不变，说明均值在过去的工艺过程中保持恒定，同时可以预测在未来的一段时间仍将保持恒定。SPC用控制图来分析统计过程的稳定性，过程受控的判断规则为:①连续25个点都在控制线之内;②连续35个点最多有1个点落在控制线之外;③连续100个点最多有2个点落在控制线之外，说明过程稳定受控;当如图1所示的控制图中的点符合下面的情况，则控制图被判断为异常，说明过程失控［14］:①1个点在A区以外;②连续9个点在中心线的同一侧;③连续6个点都递增或递减;④连续14个点交替上升和下降;⑤3个点中2个点落在中心线的同一侧的B区外;⑥5个点中4个点落在中心线的同一侧的C区外;⑦连续14个点落在C区;⑧连续8个点落在中心线的同一侧的C区外。

1．2．2 工艺能力指数

统计过程的能力是指工艺过程达到工程指标或者生产达到客户要求的参数指标的产品的能力，常用工艺能力指数(Process Capability Indices，PCI)来衡量。PCI包括过程潜力指数Cp和过程能力指数Cpk［15］，Cp指过程变异在允许范围内的潜在性，Cpk指均值与目标值的偏差程度。以双侧分布为例的Cp和Cpk表达式如下［15］:

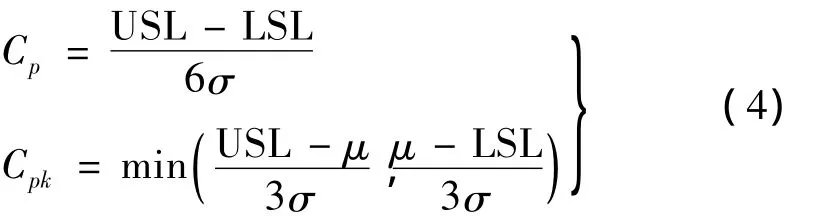
式中:μ为均值;σ为标准偏差。Cp和Cpk的关系如下:

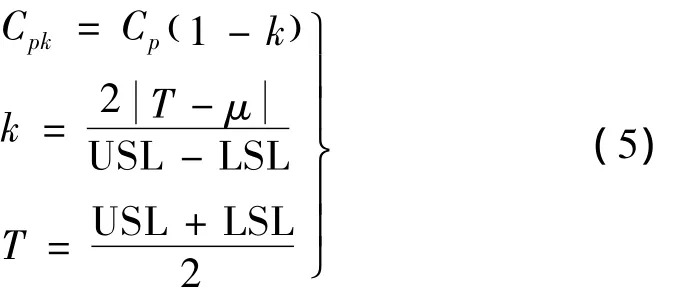
式中:μ为均值;T为目标值;k值在0～1之间，当k明显小于1，工艺过程不符合目标要求。当均值不等于目标值时，Cpk的表达式改为

式中:Cp越大，过程潜力越大，Cpk越大，过程能力越强。Cp越大，工序能力越好，Cpk越大，制程能力越好［14］。当Cp＜1．33时，变异很大，工艺需要改进，在1．33～1．67的范围内时，工艺能力较好，大于2．0说明工序能力很好。当Cpk＜1．5时，均值严重偏离目标值，制程需要改进;＞1．5时，制程能力很好;达到6．0时制程能力最好。

当 Cp达到 2．0，Cpk达到1．5 时，K 为 0．25，PCI很好，说明过程能力良好。但是Cp或者Cpk不能单独作为工艺能力指数，衡量过程具有良好的工艺能力时必须实现Cp和Cpk同时达到工艺能力指数的指标。

2 基于SPC的传感器实验设备质量控制

2．1 传感器实验测量系统

传感器实验设备的工作原理是在实验室利用传感器把非电量的温度变化转化成电阻丝的形变，进而引起电路中电压的变化，通过测量电压的变化衡量温度的变化。测量人员、传感器实验设备、测试流程、操作规范和测量环境构成传感器测量系统，在给定温度的变化时，测量系统技术要求输出电压在4．5～5．5 V。

在实验室测量环境中，由一位实验人员在一台实验设备上按照同一份操作手册进行重复测量，测量所得的数据如表1所示。

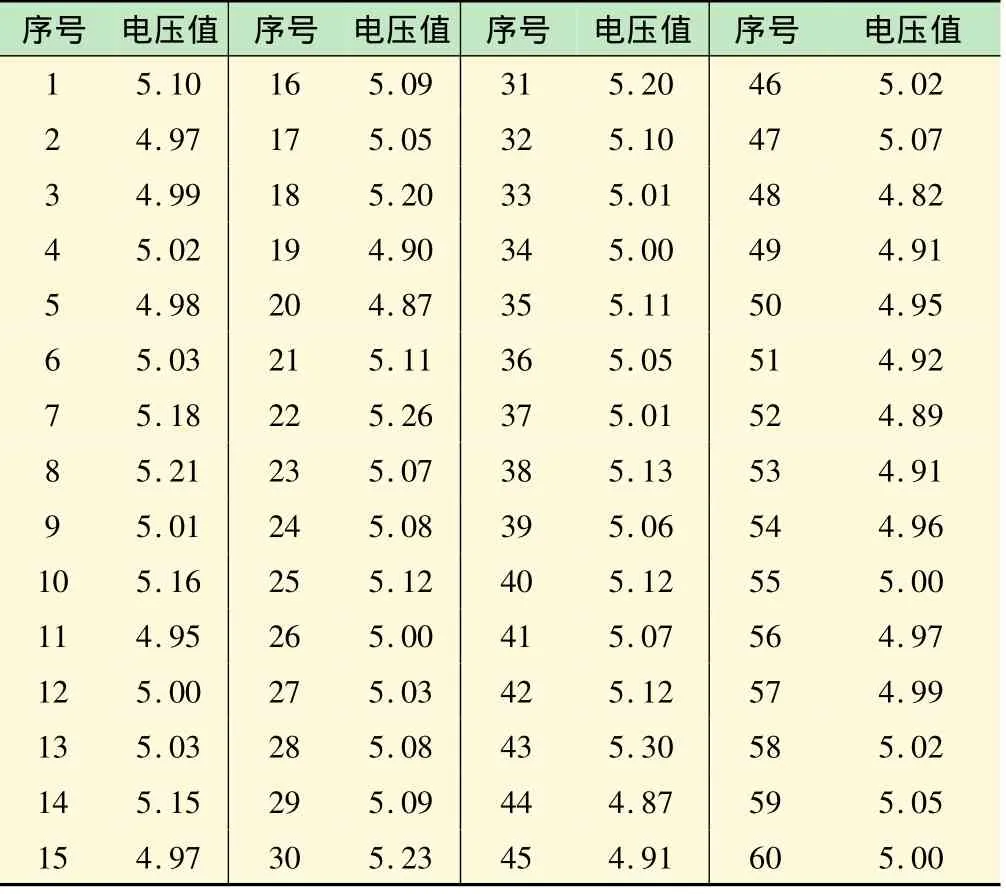
表1 测量的“电压值”

2．2 建立控制图

根据SPC的原理，建立控制图之前，必须分析实验数据的变异来源是否单一、是否正态分布和数据的独立性。

首先检验测量过程的变异来源是否单一，运用Minitab分析测量数据得到如图2所示的结果。

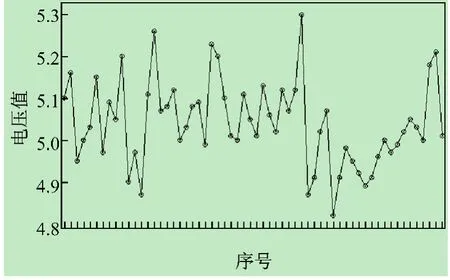
图2 测量的“电压值”的变化趋势

测量过程按照相同的操作步骤，在同一台实验设备上测量，由同一位实验人员操作，在同一个实验环境中进行，因此从图2中可以看出属于单一变异来源。其次分析是否正态分布，在Minitab软件上分析得到的结果如图3所示。

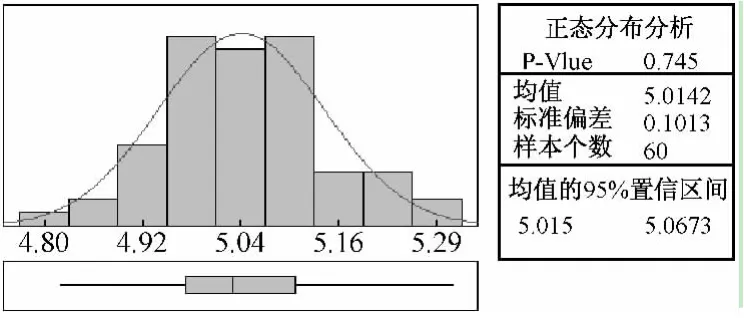
图3 测量的“电压值”的分布特性

采用假设检验判定，设定α=0．05，设定原假设H0“数据是正态分布”，备择假设HA“数据不是正态分布”，在图3中的显著性水平的可能性p值为0．745，p＞α，不能拒绝原假设H0，即接受原假设，数据是正态分布。然后分析数据是否独立，在Minitab软件上分析得到的结果如图4所示。

图4 测量的“电压值”的相关特性

从图4可见第1个点和第4个点都正向超出自相关的限度，数据正相关，可以判定“电压值”不独立。

根据SPC的工作原理，在Minitab中得到EWMA的权重分析如表2所示。

从表2中看出，权重因子λ不为零，并且λ=1－0．891 4=0．108 6。此时变异微小，需要利用残差检验数据，残差来自单一的变异来源，即测量值和目标值的偏差，因此需要查看残差的独立性和是否正态分布。查看残差的EWMA模型，在Minitab软件上分析得到的结果如图5所示。

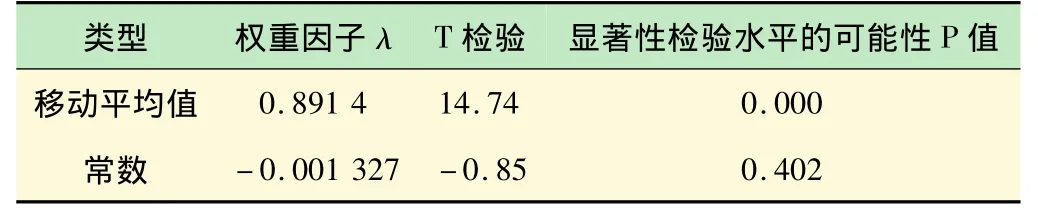
表2 EWMA的权重

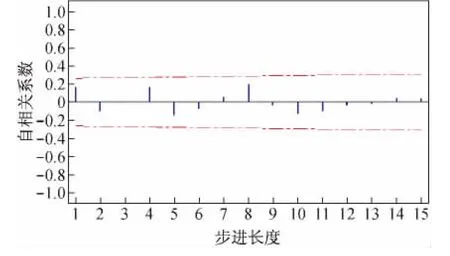
图5 残差的相关特性

从图5中可以看出，残差都在自相关的限度范围以内，数据不相关，可以判定残差独立。然后查看残差的分布特性，如图6所示。

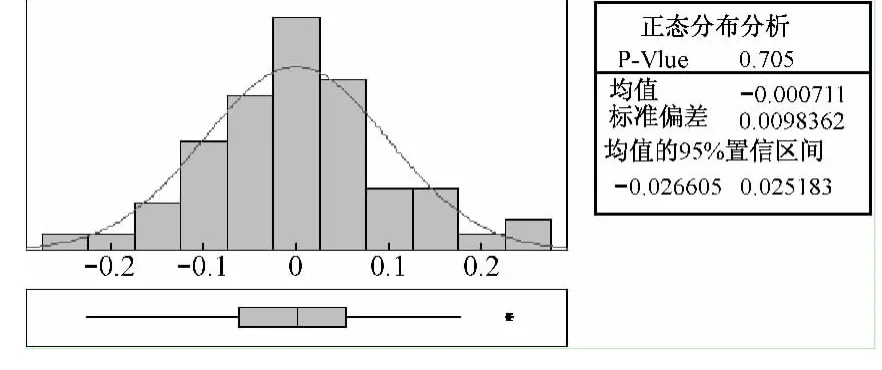
图6 EWMA模型的残差分布

采用假设检验判定，设定 α=0．05，设定原假设H0“数据是正态分布”，备择假设HA“数据不是正态分布”，在图5中的显著性水平的可能性p值为0．705，p＞α，不能拒绝原假设H0，即接受原假设，表明残差的分布是正态的。可以对残差建立控制图，如图7所示。

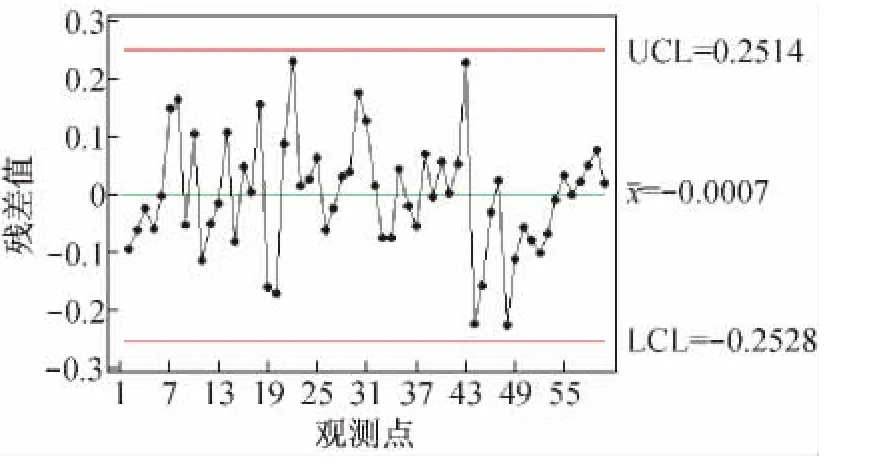
图7 EWMA模型残差的控制图

根据稳定性判断准则，从图7中可以看出，残差在控制图的控制界限内，没有异常点，处于受控状态。如果有异常点在控制区间之外，就要及时采取措施，消除异常，恢复实验设备的受控状态，从而保持实验设备运行的质量水平。

根据上面分析可看出，传感器实验设备的测量过程具有稳定性，实验设备的运行处于质量受控状态。

2．3 分析 PCI

运用SPC分析传感器实验设备的测量数据，在统计软件Minitab中得到如图8所示的结果。

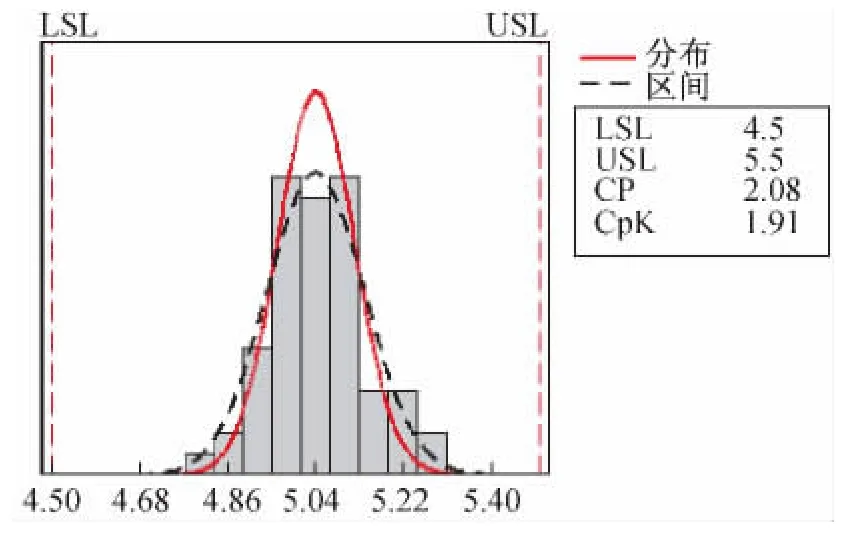
图8 测量过程的能力分析

从图中可以看出，测量过程的过程潜力指数Cp为2．08，过程能力指数 Cpk为 1．91，根据 PCI判断准则，已经符合 Cp大于2．0，Cpk大于1．5的 PCI要求，此时根据式5计算得到的k约为0．1，工艺过程符合目标要求。说明传感器实验设备具有良好过程能力。

3 结论

SPC利用真实和可靠的数据为实验设备的质量管理提供强有力的科学依据，不仅可以分析实验设备在测量过程中的稳定性，及时进行故障预警，还准确预测质量水平的趋势，提醒实验人员查找影响运行质量的不良因素。特别是在实验室测量中，单个测量值总是波动的，无法及时发现潜在质量变化，这时采用SPC对测量系统工作参数的受控状态分析就显得更加重要。

SPC研究和分析测量系统的整个运行过程，同时应用统计技术对过程的各个阶段进行监控，强调全过程的预防［16］。通过事前干预，帮助实验人员掌握实验设备的质量水平，实现实验设备的质量控制，所需成本非常低，这对探索高校实验设备的科学管理提供了有益的借鉴和示范，具有良好的经济和社会效益。

［1］ 王 静．完善实验设备的管理和使用 提高实验教学水平［J］．实验室科学，2008(5):174-175．

［2］ 卫宗超．高校实验设备综合管理现状分析［J］．管理观察，2009(7):209．

［3］ 陈 静．实验设备投资费用与风险分析［J］．财会通讯，(综合(中))，2010，2:64-65．

［4］ 杨胜科，王文科．高校实验设备可持续使用途径的探讨［J］．中国校外教育，2010(4):110．

［5］ Robert V Hogg，Elliot A Tanis，Probability and Statistical Inference［M］．6th ed．Upper Saddle River NJ07458:Prentice Hall，2001．

［6］ 陈 宏．测量系统分析在实验设备质量评价中的应用［J］．实验室研究与探索，2011，30(11):172-176．

［7］ E．Trovato，P．Castagliota，etc．Economic design of inspection strategies to monitor dispersion in short production runs［J］．Computer ＆ Industrial Engineering，2010(9):887-897．

［8］ 赵会珍，张聚涛．理解SPC控制图的关键-小概率原理［J］．统计与决策，2009(22):18-19．

［9］ 刘艳秋，时君丽．统计过程控制(SPC)在质量管理中的应用研究［J］．机电产品开发与创新，2008，21(1):69-71．

［10］ 徐 岚，刘嵘侃．SPC在多品种小批量生产线的应用研究［J］．微电子学，2007，37(5):682-684．

［11］ M．Colledani，T．Tolio．Joint design of quality and production control in manufacturing systems［J］．CIRPJournal of Manufacturing Science and Technology，2011(4):281-289．

［12］ 纪俐，王阿春．统计过程控制(SPC)在形位误差控制中的应用［J］．机床与液压，2010，38(1):68-71，38．

［13］ Michael Flynn．Regression Analysis of Automated Measurement Systems［C］．IEEE Autotestcon，2008:536–542．

［14］ 罗 军，宋德朝．基于Minitab的质量控制技术在制造过程中的应用［J］．现代制造工程，2009(2):19-21，25．

［15］ Kaya Ihsan，Kahrarnan Cengiz．Process capability analyses based on fuzzy measurements and fuzzy control charts［J］．Expert Systems with Applications，2011(4):3172-3184．

［16］ 王会良，罗 军．SPC在工序质量控制中的应用［J］．煤矿机械，2008，29(1):101-102．