基于MATLAB的集装箱多式联运方式组合模型
嵇莉莉(南京铁道职业技术学院,江苏 南京 210031)
JI Li-li (Nanjing Institute of Railway Technology,Nanjing 210031,China)
0 引 言
集装箱多式联运因其便捷、安全、费用低等特点,在国际货物运输中扮演越来越重要的角色。铁路运输一直是我国客、货运的主要运输形式。但是,在多式联运迅猛发展的今天,铁路参与国际集装箱多式联运却进展缓慢。2010年,上海洋山港完成铁水联运运量3.03万TEU,占港口集装箱吞吐量的0.3%;2011年1~9月,全国港口集装箱吞吐量12117万TEU,其中铁水联运量136万TEU,占港口集装箱吞吐量的1.1%[1]。平均而言,我国铁路参与港口集装箱铁水联运的运量不到港口集装箱吞吐量的3%,这与铁路运输在我国整个交通运输中的主导地位形成了鲜明的对比[2]。铁道部采取了一系列措施,包括客货分流、建设铁路专运线、开行集装箱班列等,以求推动铁路集装箱运输的发展。
目前,已有很多人对集装箱多式联运进行了研究,但这些研究都忽略了运输方式转换过程中可能产生的接驳费用[3-5]。我国的现实情况是,由于基础设施建设的不足,海铁联运难以实现无缝对接,货主为了规避海铁联运中因接驳运输而额外产生的装卸及运输费用,大多选择了“海—公”联运的方式,使得铁路在多式联运中的作用不能充分发挥,也影响了多式联运方式选择的决策。本文以实现运输成本最小化为目标,考虑到我国大部分港口的基础设施建设难以实现海铁联运无缝衔接的现实情况,将公路接驳运输纳入多式联运系统的考虑范围,建立了多式联运方式选择模型。同时给出了求解此模型的一个算法,此算法相较于智能算法[6-9]简单且容易实现,并可以保证在有限步收敛。最后用MATLAB软件对算法进行了数值仿真,并根据计算结果,对铁路如何更好地参与集装箱多式联运的问题提出建议。
1 多式联运方式选择模型
多式联运可以看成是一个由若干个节点和连接节点间的箭线构成的网络模型,如图1所示。节点1到达运输方式是公路,发送运输方式也是公路,即在节点1不发生换装。节点2到达运输方式是公路,发送运输方式是铁路,即在节点2做公路—铁路的换装。这个过程可以在铁路集装箱办理站完成,公路和铁路的换装可以实现无缝衔接。节点3的到达运输方式是铁路,发送运输方式是水路,即在节点3做铁路—水路的换装。由于基础设施建设的不完善,我国大部分集装箱码头都没有直接连接铁路线,货物在节点3上的换装不能实现无缝衔接,需要通过公路接驳。例如上海洋山港集装箱码头,通过铁路集运的集装箱货物只能运到芦潮港集装箱中心站,接下来30多公里的跨海大桥需要由集卡通过公路完成。实践中,节点3上,增加的换装作业以及接驳作业会增加多式联运的总费用和总时间,也可能会影响到多式联运经营人对多式联运组合方式的选择。本文基于海—铁不能实现无缝衔接的情况,以费用最小化为目标,建立多式联运方式选择模型。

图1 多式联运节点换装示意图
1.1 模型假设
根据以上描述,对模型做如下假设:
(1)由于集装箱运输对装卸设备有特殊要求,因此,换装只发生在特定中转站点;且根据通常的做法,做如下限定:公铁换装发生在铁路场站;公水换装发生在港口码头;铁水换装不需接驳发生在港口码头,需换装的分别发生在铁路场站和港口码头。
(2)两个节点之间可选的运输方式有3种,即公路、铁路、水路。
(3)转换运输方式时,如需接驳,一般采用公路运输作为接驳方式。
(4)不考虑货运量对运输价格及运输时间的影响。
(5)运量不可分割,即两个城市之间只能选择一种运输方式。
(6)不考虑运输能力的限制。
1.2 参数说明

1.3 模型建立
以多式联运费用最小化为目标构建目标函数:
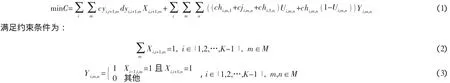

其中,目标函数(1)表示要求多式联运总的运输费用最小,包括运输费用、换装费用和必要时的接驳费用;约束条件(2)表示两个节点之间只能选择一种运输方式;约束条件(3)表示从i-1节点到i节点选择m方式运输,从i节点到i+1节点选择n方式运输,则在i节点要进行运输方式m和n的转换,即保证运输时连续的;约束条件(4)和(5)是时间约束,表示运输时间必须控制在 [tmin,tmax]之间。
2 MATLAB算法设计
MATLAB是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平[10]。本节利用MATLAB程序设计语言,给出了求解此模型的一个算法,此算法相较于智能算法简单且容易实现,并可以保证在有限步收敛。算法主要步骤如下:
第一步,输入 cyi,i+1,m、dyi,i+1,m、tyi,i+1,m、cji,m,n、Ui,m,n、chm,n、thm,n、dji、tji、vm。
第二步,计算多式联运货物在途费用。

第三步,计算多式联运货物在站点的换装和接驳费用。

第四步,选择最优方案。在总时间T∈ [Tmin,Tmax]的情况下,如果计算单箱运费C<Cmin,记录运费Cmin=C,记录总时间,记录各节点选择的运输方式。
3 数值仿真
例:假设集装箱货物装运地为成都,途径郑州、南京,最终到达上海洋山港装船出口。本节为该批货物选择适合的运输方式,使其在满足时间约束的基础上实现运输成本的最小化。为了使问题简单起见,本节定义节点K=4,表示有成都、郑州、南京、上海4个节点城市。
仿真中需要的数据如下:
各节点间集装箱多式联运各种运输下的运输距离如表1所示。表1中,南京到上海的公路距离包括了连接洋山港的东海大桥距离,铁路距离为南京西站到上海芦潮港铁路集装箱中心站距离,水路运输距离为南京港到洋山港距离。各种运输方式下,运载工具的速度如表2所示。

表1 集装箱多式联运各种运输方式的运距表单位:千米

表2 运载工具速度表单位:千米/小时
针对公路、铁路、水路三种运输方式,分别各采集了40组数据(运输距离—运输费用)。用MATLAB软件的polyfit命令对数据进行线性拟合,得到各种运输方式下运费的计算公式。
(1)公路集装箱单箱单位距离运输费用计算公式:

(2)铁路集装箱单箱单位距离运输费用计算公式:

(3)水路集装箱单箱单位距离运输费用计算公式:

根据费用公式(6)~(8)和表1中数据,计算得到集装箱单箱单位距离运输费用如表3所示。
各种运输方式中转站换装费用如表4所示。

表3 多式联运各路段单箱单位距离运输费用单位:元
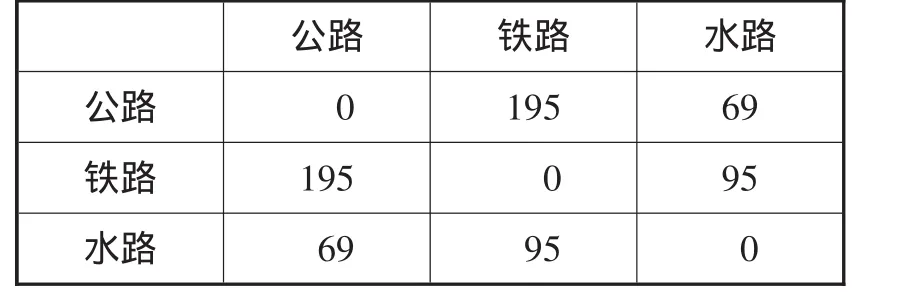
表4 换装费用单位:元/箱
换装过程中,各节点接驳运输距离如表5所示。
中转站换装时间[11]如表6所示。

表5 公路接驳运距单位:千米

表6 中转站换装时间表单位:小时
对上述数据利用MATLAB软件进行程序设计,得到运输方式组合策略如表7所示。
分析表7数据,可以看到,在不同的时间约束条件下,多式联运方式组合的策略有所不同,其对应的成本也有较大差别。货主对送达时间上的要求会影响到多式联运方式组合的决策。从时间的角度来看,公路较铁路运输方式具有优势,但是,只有在对时间要求极强的情况下,公路的这种竞争优势才能凸显,铁路参与多式联运仍有很强的竞争力。
4 铁路参与多式联运的建议
4.1 合理选址铁路集装箱办理站
为了探讨铁路如何更好地参与多式联运的问题,在程序运行过程中,本文改变芦潮港铁路集装箱中心站的选址来进行试验。结果显示,海铁联运中,公路的接驳距离有一个临界值,当接驳距离小于这个临界值时,铁路运输有优势,当接驳距离大于这个临界值时,公路运输更有优势。也就是说,从费用的角度来看,短距离的接驳运输不影响铁路的竞争优势。这个临界值的确定跟铁路和公路的运价,以及货物在站点内的留存时间和作业成本等有关。随着铁路运价的上升,以及公路运价的下跌,这个临界值趋于减小。
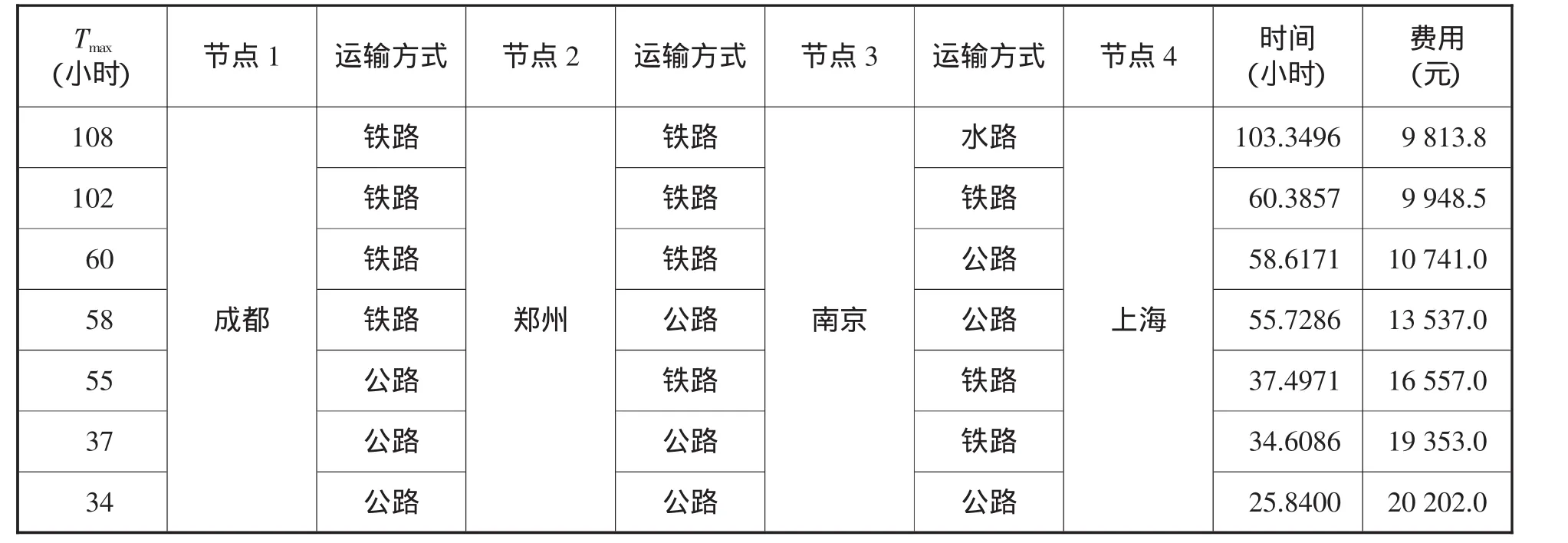
表7 多式联运方式组合
因此,对于铁路专运线不能延伸到达的港口码头,根据本文给出的算法,可以找到海铁联运接驳的临界距离,应该在以港口为中心,以该临界距离为半径的范围内,建设铁路集装箱办理站。办理站应具有集运堆存、通关、保税监管等功能。出口货物在办理站办结出口手续,按照海关监管货物完成接驳运输并装船出口;进口货物卸船后不落地,按照保税货物在海关监管下疏运至铁路集装箱办理站,与货主的交接在办理站完成。铁路集装箱办理站完善的业务功能和合理的选址,有助于铁路与其他运输方式协同发展。
4.2 缩短铁路运输服务响应时间
铁路在参与多式联运中存在的主要问题不是成本,无法实现海铁的无缝衔接也在其次。铁路运力紧张、货物等待时间长,以及服务质量和市场意识薄弱等,才是铁路参与多式联运亟待解决的问题。本文对运输工具转换过程中的货物等待时间做了简化处理,而事实上,由于铁路运力紧张,在开展集装箱运输过程中,常常出现有货无箱、有箱无车、有车无计划的现象,很难满足货主对运输时间的要求。这往往正是货主弃铁路而选择其他方式的主要原因。调整模型中铁路站点的货物换装时间,当换装等待时间增加1天,铁路相对水路运输将失去优势。而目前,集装箱货物在铁路站点的等待时间往往是超过1天的。因此,提高铁路集装箱运输能力,缩短铁路运输服务响应时间,是铁路更好地参与多式联运的关键。
4.3 引入灵活的国际货运代理机制
集装箱多式联运通常是由多式联运经营人组织全程运输,货主不直接与运输企业联系。多式联运经营人建立自己的运输网络,通过在各地的运输代理人与各实际承运人达成运输协议,完成货物运输业务。
长期以来,海运货代业务已经发展的较为成熟,一个海港城市拥有的货代公司大多数以万计。多式联运经营人想要与货代取得联系或订舱都是比较容易的。但是铁路运输行业由于长期以来市场意识缺乏,铁路货代的入行门槛比较高,一个集装箱货运站的货代业务就掌握在少数几家公司手中。这种现象增加了多式联运经营人选择铁路运输方式的难度,严重影响了铁路参与多式联运的主动性。因此,参考海运货代的运作模式,与更多货运代理企业建立业务关系,是铁路走向市场,更好地参与多式联运的重要途径。
[1]董红梅.洋山港海铁联运模式的现状及发展[J].物流工程与管理,2011(10):27-29.
[2]张戎,秦明霞,艾彩娟.芦潮港集装箱中心站海铁联运发展对策研究[J].铁道货运,2010(10):12-17.
[3]李成,盖宇仙,颉栋栋.构建铁路物流中心为核心节点的多式联运系统[J].交通科技与经济,2010(4):4-7.
[4]周跃.集装箱多式联运运输决策与协调问题的研究[D].南京:河海大学(硕士学位论文),2006.
[5]韩俊,徐奇,靳志宏.动态规划的集装箱多式联运系统运输方式组合优化[J].武汉理工大学学报(交通科学与工程版),2010(8):661-664.
[6]陈相东,刘彦良,王鹏涛,等.多种运输方式模型优化及求解[J].天津师范大学学报,2005(9):66-69.
[7]贺竹磐,孙林岩,李晓宏.时效性物流联运方式选择模型及其算法[J].管理科学,2007(2):8-12.
[8]李浩.基于遗传算法的大件物流运输方案选择优化研究[D].青岛:中国海洋大学(硕士学位论文),2011.
[9]于瑞菊.集装箱多式联运系统运输组合优化与分级优化研究[D].青岛:青岛大学(硕士学位论文),2010.
[10]Cleve B.Moler.MATLAB数值计算[M].北京:机械工业出版社,2010.
[11]靳志宏.物流调度与协调[M].北京:中国物资出版社,2008.

