基于ACA的军事物流车辆配送路径优化研究

谭云恩，张 亮，杨 霞，甄瑞杰TAN Yun-en,ZHANG Liang,YANG Xia,ZHEN Rui-jie

（1.华北物资采购局，天津 300182；2.军事交通学院，天津 300161；3.预备役五七四团，辽宁 风城 118100）

(1.NC Material Procurement Agency,Tianjin 300182,China;2.Military Transportion College,Tianjin 300161,China;3.Reserve the 574 Regiment,Fengcheng 118100,China)

军事物流是指军事力量在生活、训练、执勤及作战时所需军事物资经过筹措、运输、仓储、供应等环节，最终送达部队被消耗使用，实现其空间与时间转移的全过程，是社会物流系统中的重要分支。军事力量正是由于通过军事物流源源不断地供应其所需物资，才得以有效地开展军事行动，才得以强化训练提高战斗力。而军事物流配送作为军事物流的重要组成部分，它指的是在一定的区域范围内，根据部队需求，对军用物资进行拣选、组配等作业，并按时送达部队指定地点的物流活动。我军后勤保障现实行的是联勤保障体制，各大军区都设有联勤部，负责通过军事运输对辖区内各部队的物资供应和补充。通常军事运输的方式主要有五种：铁路、公路、水路、航空和管道，目前公路运输仍然是我军物资运输的主要运输方式。而据初步调查研究，在我国军事物资供应过程中，每年由于不合理运输而造成的额外运输量高达数百万吨。可见，车辆配送路径优化选择问题已经成为制约保障能力生成的重要因素之一。

1 军事物流配送路径优化模型

车辆配送路径优化问题一般可以这样描述：从某军事物流配送中心用多辆配送车辆向多个部队用户运送物资。每个部队用户的位置和货物需求量一定，每辆车的载重量一定，其一次配送的最大行驶距离一定。要求合理安排车辆配送路线，使目标函数得到最优。并满足以下条件：

（1）每条配送路径上各部队用户需求量之和不超过配送车辆的载重量；

（2）每条配送路径的长度不超过配送车辆一次配送的最大行驶距离；

（3）每个部队用户的需求必须满足，且只能由一辆配送车送货。

设配送中心需要向k个部队用户送货，每个部队用户的货物需求量是gi（i=1,2,…,k ），部队用户i与部队用户j 之间的距离为dij，每辆配送车的载重量是Q，且gi＜Q。首先为了安排路线需要对要使用的车辆数有一个估计。在现实情况中，货物装（卸）车越复杂，约束条件越多，一辆车的实际载货量就越小。可由用户选择参加运输的车辆数，或由下面公式来确定需要的汽车数：

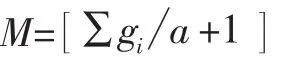
M为所需汽车数，［］表示取整，a为参数，0＜a＜1，约束条件越多，货物装（卸）车越复杂，a值越小。实际应用中，可用人机对话来确定a值。

目标函数：

CR为每辆车出动的固定费用，Cm为车辆的每公里费用；式（2）表示每一个点都恰好位于某一路径之中；式（3）表示某车到达一个点后也必然离开这个点；式（4）表示对车辆的负载限制；式（5）保证了每个点的运输任务仅由一辆车完成，而所有运输任务由M辆车协同完成；式（6）保证每一条路径起、止于中心站。

2 求解军事物流配送问题的ACA算法

1991年，意大利学者M.Dorigo等人从生物进化的机理中受到启发，通过模拟自然界蚂蚁寻径的行为，提出了一种全新的模拟进化算法——蚁群算法。

2.1 蚂蚁算法的原理

蚂蚁觅食时，对于从蚁窝到食物源的诸多途径，开始时不同的蚂蚁会选择不同的路径，但最后，几乎所有的蚂蚁都会找到同一条最短的路径。蚂蚁虽没有视觉，但运动时会在通过路径上释放出一种特殊的分泌物——信息素，而且能感知这种信息素的存在及强度并朝该物质浓度高的方向运动，这些信息素既会随通过的蚂蚁数量增加而增加，也会随时间的流逝而按一定的函数关系消逝，这样便形成了一个正反馈机制，最终整个蚁群会找出最优路径。同时蚁群还能够适应环境的变化，当蚁群的运动路径上突然出现障碍物时，蚂蚁也能很快地重新找到最优路径。蚁群算法就是模拟上述蚂蚁觅食行为，设计虚拟的人工蚂蚁，使其随机搜索不同的路径，并留下会随时间变化而蒸发的“信息素”，根据“信息素”强度来寻找最短路径。但人工蚁群和自然界蚁群是有区别的，区别在于人工蚁群具有一定的记忆能力，它能够记忆已经访问过的节点；另外，人工蚁群在选择下一条路的时候并不是完全盲目的，而是按一定的算法规律有意识地寻找最短路径。

2.2 蚂蚁算法的基本模型

基于蚂蚁算法的原理，设n是部队用户数，k是蚂蚁的数目，dij（i,j=1,2,…,n ）表示用户i到用户j所需的路径长度，bi（t）表示t时刻位于客户i的蚂蚁数目。则有表示t时刻客户i,j之间的信息素。初始状态下，各条路线上信息素浓度相等，设τij（0）=C（C为常数）。蚂蚁k（ k=1,2,…,m ）在移动过程中，根据各条路线上的信息素决定前进方向。

式中：Q是一个常数，其数值由具体实验给定。

3 仿真结果

某部队有1个配送中心和8个配送点，各配送点的货运量为g（单位：吨）。各需求点的需求量在0,［］4间随机生成，使单辆车能承担更多的运输任务。满载系数a取0.85，默认交叉率为0.6，默认变异率为0.02。配送中心与配送点位置及需求量如表1。

根据各需求点的需求量计算出需要的汽车数为：

表1

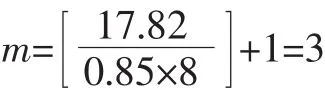
应用蚂蚁算法对以上问题进行求解，经过构造蚂蚁算法函数得出最佳路径为：

子路径1：0→8→7→4→0

子路径2：0→6→0

子路径 3：0→5→3→1→2→0

4 结束语

精确保障越来越重要、艰巨和复杂，如何有效提高精确保障能力已成为研究的热点问题。但现有装备、保障力量有限，在现有的基础上，对精确保障决策进行优化特别是对车辆配送路径选择问题进行优化是提高精确保障能力的事半功倍的重要手段，而蚂蚁算法能够较快发现和搜索到最优路径，从而合理地安排配送车辆的行车路线以达到缩短运距，提高保障效能。

[1]周勇，陈洪亮.蚁群算法的研究现状及其展望[J].微型电脑应用，2002,18(2)：5-7.

[2]潘震东，唐加福，韩毅.带货物权重的车辆路径问题及遗传算法[J].管理科学学报，2001,10(3)：23-28.

[3]万荣.信息化条件下军事物流配送[D].重庆：重庆后勤工程学院，2008.

[4]陶羿，朱建清，李明.军事物流选址分配模型及遗传算法优化[J].信息工程大学学报，2001,8(1)：110-115.

[5]周屹，李海龙，王锐.遗传算法求解物流配送中带时间窗的VRP问题[J].吉林大学学报（理学版），2008,46(2)：300-303.

[6]高尚，钟娟，莫述军.连续优化问题的蚁群算法研究[J].微机发展，2003,13(1)：21-22.

[7]DORIGO M,MAMIEZZO V,COLORNI A.Ant Sys-tem：optimization by a colony of cooperating agents[J].IEEE Transactions on SMC,1996(1)：554-558.