正多边离散环路磁场积分问题分析

李深旺，张国庆，郭志忠，于文斌，宋 平，黄华炜

(1.哈尔滨工业大学电气工程及自动化学院，150001哈尔滨;2.国网上海市电力公司，200122上海)

光学电流互感器(optical current transducer，OCT)基于法拉第磁光效应测量电流，其实质是沿传感光路的磁场积分［1-2］.按照传感光路结构的不同，光学电流互感器可分为闭合光路型光学电流互感器和直通光路型光学电流互感器.直通光路型光学电流互感器采用磁光玻璃作为光学传感材料，结构简单，可以有效解决光学电流互感器存在的测量精度的温度漂移和长期运行稳定性差的问题，极具实用前景［3-7］.

直通光路型光学电流互感器面临着抗外磁场干扰能力差的问题.安培环路定律的要点是闭合环路，而直通光路型光学电流互感器的光路被分割为若干分离的直线段，变成离散环路，失去了连续闭合性，属于离散环路磁场积分范畴，不满足安培环路定律［8］，因此，其抗外磁场干扰能力较差.抗外磁场干扰能力差成为阻碍直通光路型光学电流互感器实用化的关键技术障碍.目前解决这一问题的主要方法有:磁屏蔽技术、集磁环聚磁技术、传感头结构优化、差分式传感技术等［3，9-14］.这些方法可以取得一定的抑制外磁场干扰的效果，但效果有限，不能从根本上解决直通光路型光学电流互感器抗外磁场干扰能力差的问题.

文献［12-13］研究了安培环路定律的等价解环条件:特定条件下离散环路的磁场积分仍满足安培环路定律.本文在文献［12-13］的基础上研究正多边离散环路磁场积分问题，对离散安培环路定律进行了初探，并定义了离散环路磁场积分的两个模型:正多边离散环路Sm模型和Sm正分布的mSm模型，通过对两种模型零和P点特性的研究，提出了Sm模型的零和定理、mSm模型的互易定理，形成了以零和P点为基点的、仍然遵守安培环路定律的正多边离散环路磁场积分理论体系，为光学电流互感器的零和御磁技术奠定了重要的理论基础.本文的研究为解决直通光路型光学电流互感器的抗外磁场干扰技术难题提供新的方法.

1 离散安培环路定律

离散环路磁场积分问题来自光学电流互感器抵御外磁场干扰的零和御磁技术［12-13］.与磁屏蔽技术不同，零和御磁技术不是阻止外磁场的进入，而是让其进入但失去干扰作用，简捷有效，如图1所示.

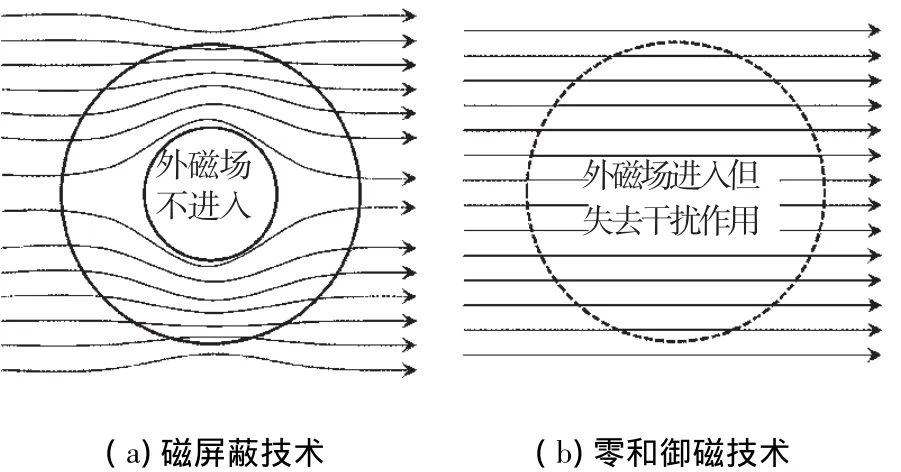
图1 零和御磁技术与磁屏蔽技术的不同

安培环路定律表明，磁场环路积分与环路外的电流无关，即

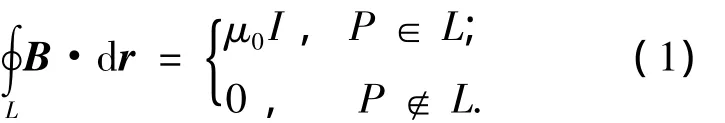
式中:B为磁感应强度;P为载流导体置放点;L为闭合环路;μ0为真空磁导率;Ⅰ为环内电流.

1.1 约定

约定1:离散环路.保留了若干相互分离有向线段(直线或者曲线)lk(k=1，2，…，m)的环路，记作L.

约定2:参考方向.相对离散环路L内的任意点，逆时针方向为有向线段正方向，如图2(a)所示.

约定3:P点、P点张角.P点是置放载流导体的几何点;P点张角是P点向有向线段两个端点张开的角度，记为αk(k=1，2，…，m)，简称张角.如图2(b)所示.

约定4:张角符号.张角αk(k=1，2，…，m)的符号为沿有向线段lk的磁场积分符号，即

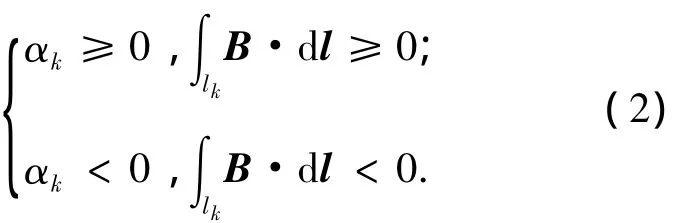
在式(2)约束条件下，对于环内P点，有

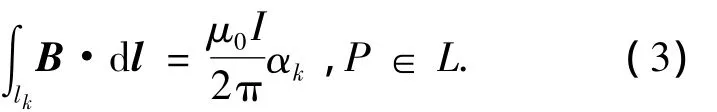
图2 离散环路

约定5:零和P点.满足下式的P点为零和P点，零和P点是对离散环路磁场积分不起作用的几何点.显然，在上述约定下零和P点存在且只存在于离散环路之外.

1.2 离散安培环路定律

在1.1节的约定下，容易理解如下的离散安培环路定律.

离散安培环路定律:若环外电流置放在零和P点上，离散环路磁场积分可表达为

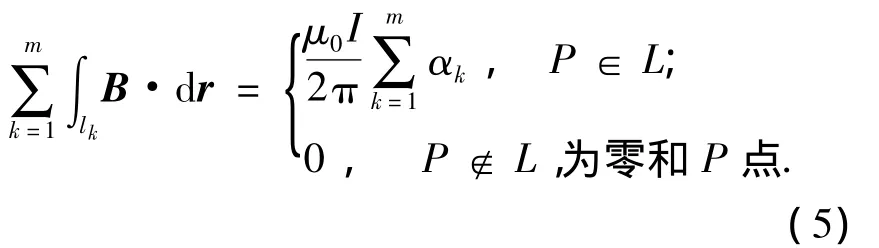
其中:μ0为磁导率，Ⅰ为环内电流.

2 Sm模型及零和定理

2.1 定义

定义1正多边离散环路模型.Sm(m≥2)表示m条有向线段组成的离散环路，并满足以下条件:1)有向线段lk(k=1，2，…，m)，隔边相望，取正2m边形的m条边;2)有向线段方向遵守1.1节的约定2.

2.2 约定

约定6:Sm坐标系.Sm坐标系原点取其中心点O，横轴为原点O与某一有向线段li中点的连线.

约定7:P线、P线角.P线是Sm原点O指向环外P点的矢量;P线与Sm横轴x的夹角θ叫P线角.

约定8:零和P线、无向零和P线.零和P线是零和P点对应的P线;不考虑方向的零和P线为无向零和P线.

约定9:线段角.Sm原点0向有向线段两个端点张开的角度，记为φ，显然有

2.3 张角向量

如图3所示的Sm模型，对于环外任意P点，有

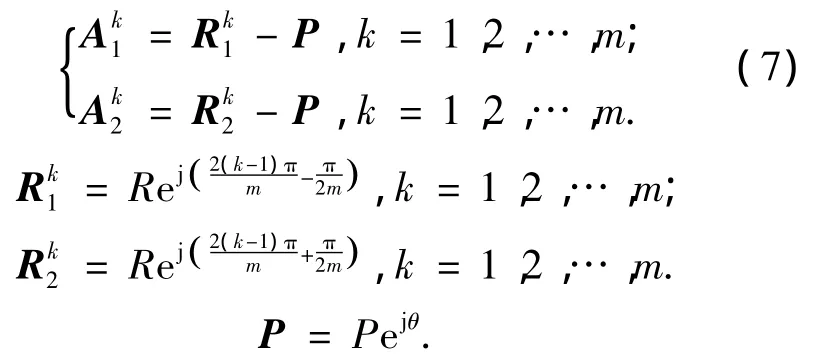
其中:R为Sm外接圆半径，P为P线幅值.

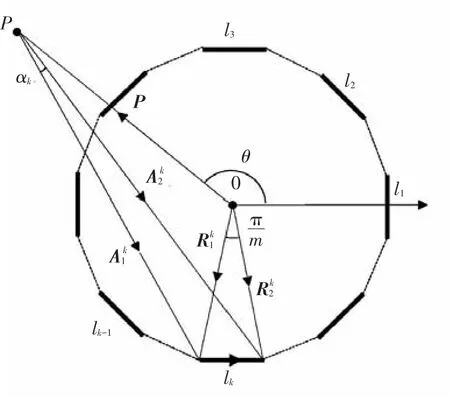
图3 Sm模型

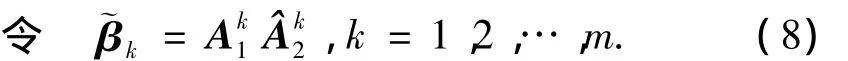
由于

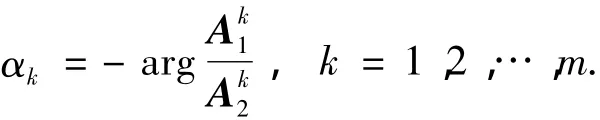
因此

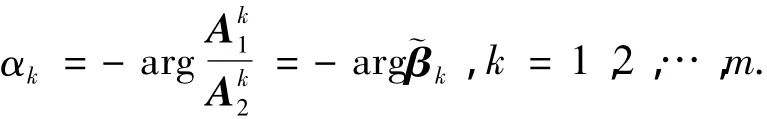
将式(8)展开

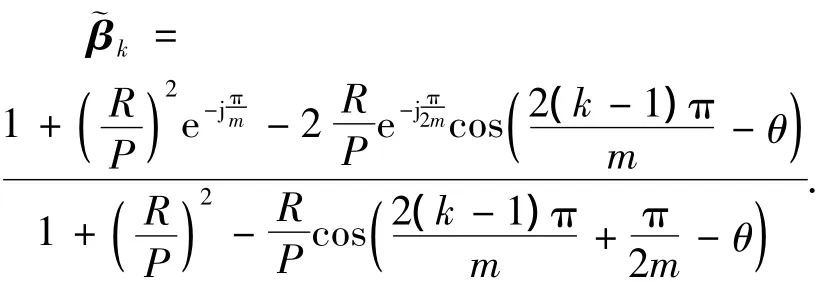
考虑到

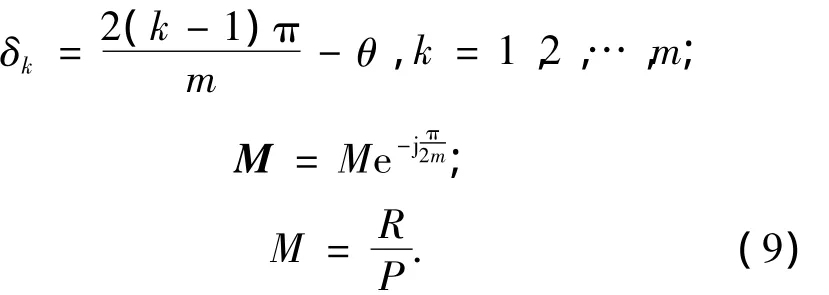
可得到张角向量

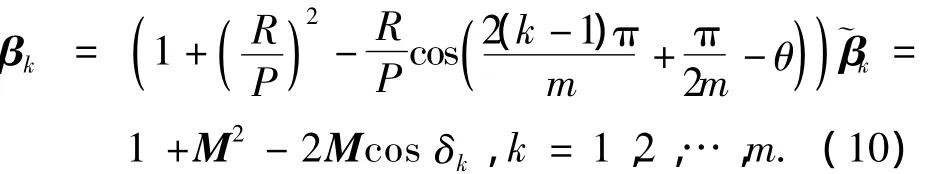
令

显然有

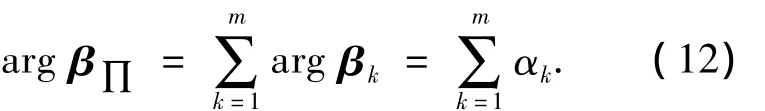
由式(12)可得

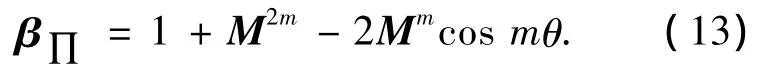
对式(13)证明如下:对于以下的复因子序列

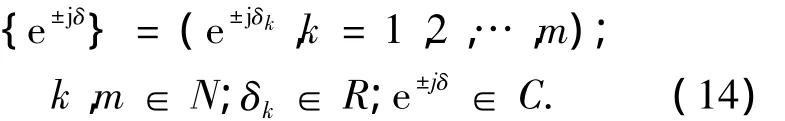
设式(14)的C积和是复因子以Ckm方式相乘后的累加，记作Ckm{e±jδ}，上标k叫C积和的阶，k是复因子序列{e±jδ}的维数，也是C积和的最大阶数，δk是角度，约定C0m{e±jδ}=1.若复因子序列{e±jδ}的角度序列为

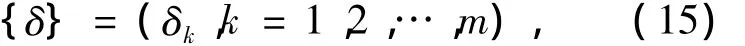
等分圆周，即满足条件

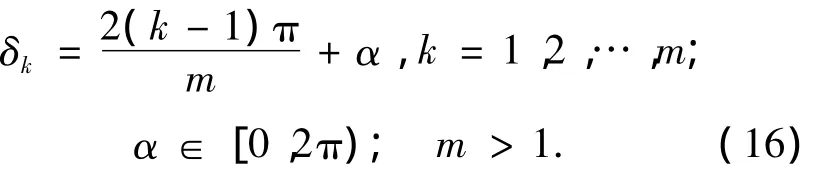
则C积和的取值为

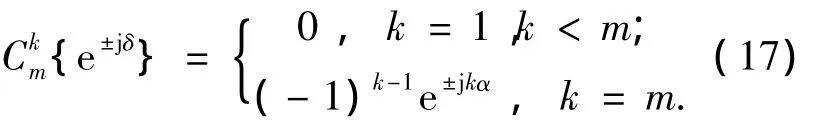
若复因子序列{e±jδ}的元素对应的函数为

且序列{δ}等分圆周，即满足式(15)，根据Euler公式有

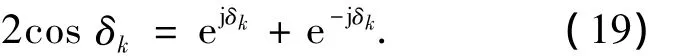
得到

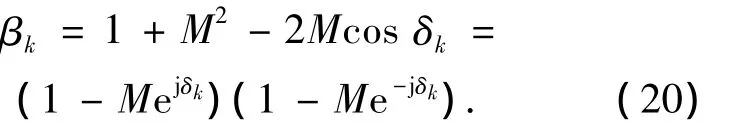
因此

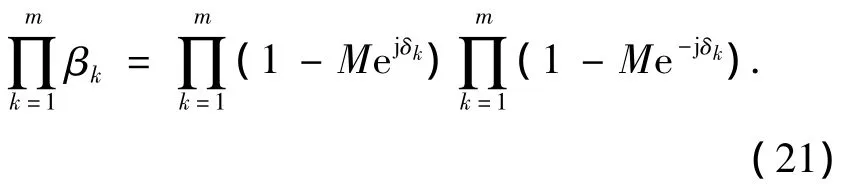
注意到

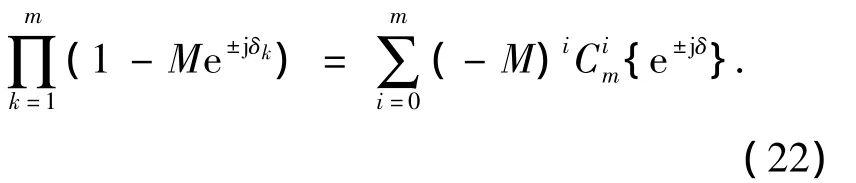
如此可得

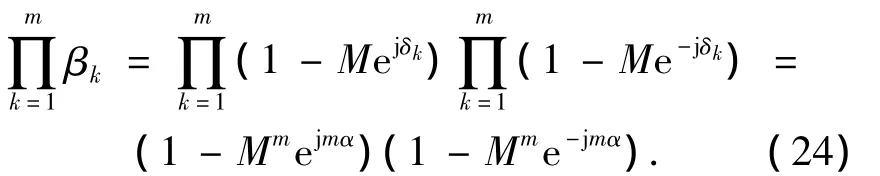
即为

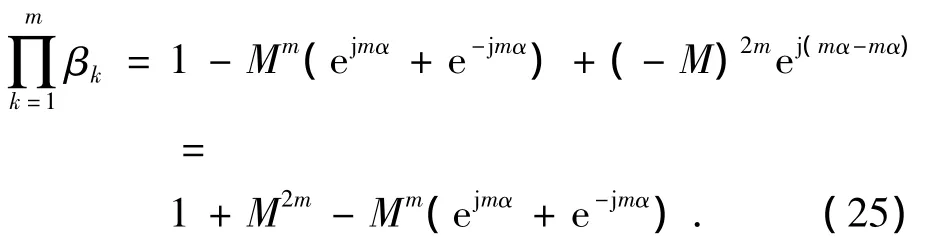
再根据Euler公式，得到

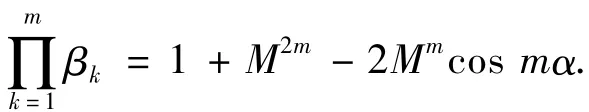
证明完毕.

2.4 零和定理

定理1零和定理.对Sm模型，满足如下P线角关系的2m条P线为零和P线.

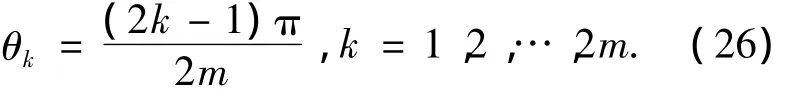
证明容易理解如下等价关系:

结合式(13)，可得

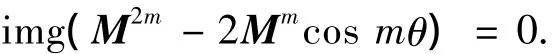
考虑M的取值，上式等价为

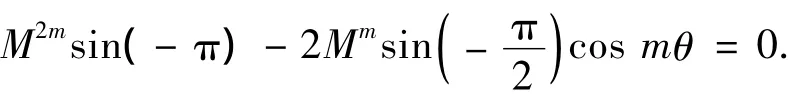
就是

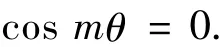
于是

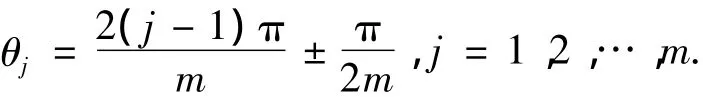
将上式展开，并划分为如下两个集合:

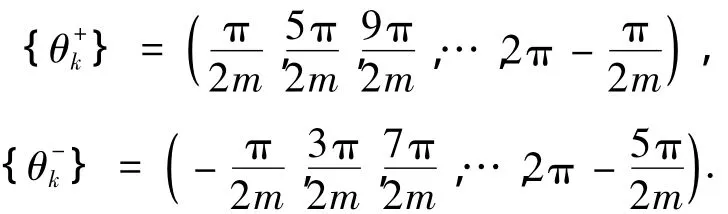
考察发现，两个集合可统一记作式(26)的形式.证明完毕.

推论Sm模型有m条无向零和P线.

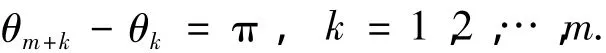
证明根据式(26)，有即第m+k条和第k条零和P线的方向相反.因此Sm有m条无向零和P线.根据零和定理知道，Sm模型的零和P线具有如下基本性质:1)零和P线由且仅由P线角决定;2)有向线段端点与Sm原点的连线是零和P线的一部分;3)零和P线在离散环路外的任意点都是零和P点.

2.5 零和定理应用举例

本节以m=6为例，讨论Sm模型及零和定理在零和御磁技术中的应用.图4为S6模型的示意图.取6块相同的磁光玻璃材料按照S6模型布置，即6块磁光玻璃的传感光路分别与S6模型的有向线段l1、l2、l3、l4、l5、l6重合，磁光玻璃的通光方向与约定2的方向相同，从而构成S6结构OCT.下面分析S6模型的零和御磁问题.

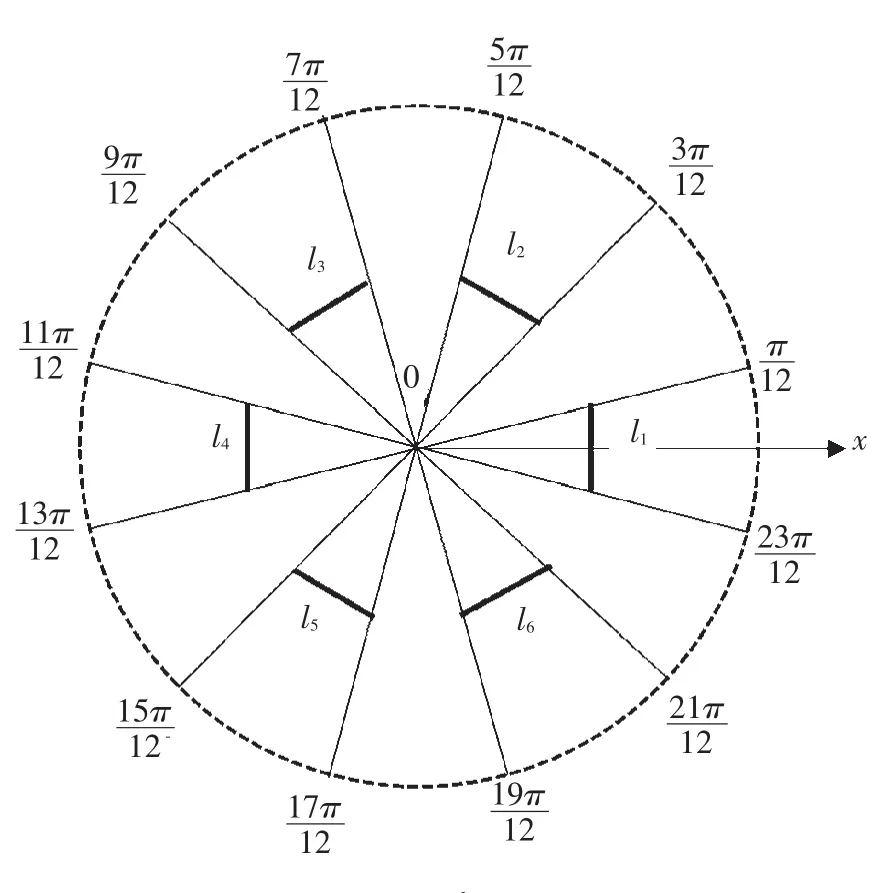
图4 S6模型

由式(26)可知，S6模型有12条零和P线，这些零和P线将圆周均匀分割为12等份，如图4所示.将待测电流ic布置于OCT的中心、干扰电流ig布置于OCT的零和P线上，则OCT对待测电流ic产生磁场Bc的积分结果为

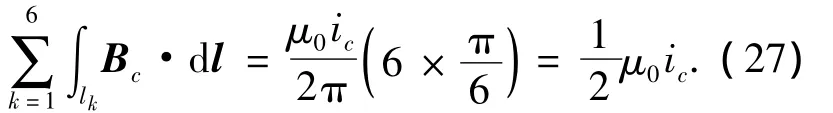
OCT对干扰电流ig产生磁场Bg的积分结果为

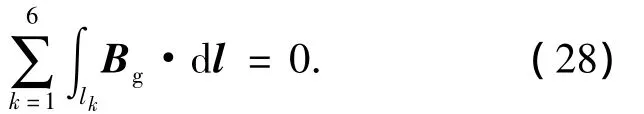
由式(27)、(28)可见，干扰电流ig产生的磁场Bg对OCT的测量结果没有贡献，这意味着干扰电流产生的磁场虽然可以通过OCT的内部但完全失去了干扰作用，采用零和御磁技术设计的OCT可以实现对待测电流ic的无干扰测量.

Sm模型适用于存在一个或多个干扰电流情况下对待测电流的抗干扰测量.

3 mSm模型及互易定理

3.1 定义

定义2Sm正对称分布模型mSm.mSm是m个相同Sm组成的几何图形，每个mSm的原点为正m边形的一个顶点，且满足不重叠条件

其中:D为相邻Smk中心点的距离.mSm模型描述m个Sm同时存在的正对称分布情况.

3.2 互易定理

mSm每个顶点有m-1条顶点连接线，它们将内角分割为m-2个相等的角，取值为

显然，此角度恰好等于式(6)的线段角φ，完全吻合地放置顶点为原点的Sm.一个Sm有m条无向零和P线，其中的m-1条线为mSm顶点间的连接线，剩余1条是mSm外接圆在顶点的切线.如此，任意Sm原点都处在所有其他Smk(k=1，2，…，m;k≠i)零和P线的交点上.这样，如果mSm中任意两个Sm互换位置，必然是原点与零和P点的互换.

定理2互易定理.如果mSm中任意两个Sm位置互换，则原点与零和P点互换:其中一个Sm的原点成为另一个Sm的零和P点，反之亦然.

3.3 互易定理应用举例

本节以m=6为例，讨论mSm模型及互易定理在零和御磁技术中的应用，6S6模型的示意图如图5所示.

将6个S6结构的OCT按照6S6模型布置，即:将6个S6结构的OCT布置于正六角形的6个顶点，各个顶点与S6模型OCT的中心重合，调整各个OCT的安装角度使其满足定理2，从而构成6S6结构的OCT组合.下面分析6S6模型的零和御磁问题.

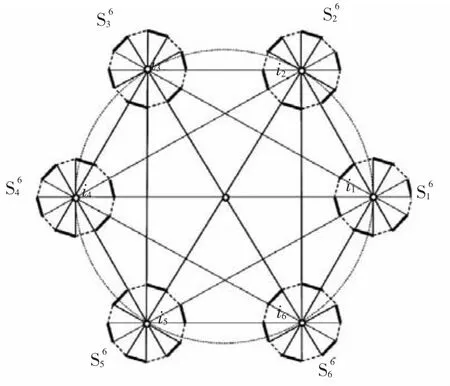
图5 6S6模型

将6个待测电流ij(j=1，2，…，6)分别布置于6个S6结构OCT的中心，则对于任意一个S6结构OCT而言，其他5个电流都是干扰电流，但是这5个干扰电流都位于它的零和P线上.以S61为例，i1为待测电流，其他电流为干扰电流，则S61对待测电流i1产生磁场B1的积分结果为

对干扰电流ij(j=2，3，4，5，6)产生磁场Bj的积分结果为

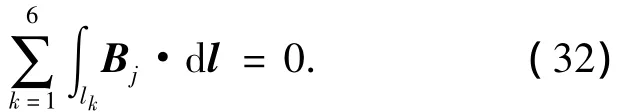
由式(31)、(32)可见，干扰电流ij产生的磁场Bj对S61的测量结果没有贡献，这意味着干扰电流产生的磁场虽然可以通过OCT的内部但完全失去了干扰作用，采用零和御磁技术设计的OCT可以实现对待测电流i1的无干扰测量.同理可知，该结论对于S6j(j=2，3，4，5，6)同样成立，此处不再赘述.

mSm模型适用于对多个电流进行测量且各个待测电流互为干扰电流的情况.

4 拓展模型

定义3拓展Sm模型.若端点位置不变，无论有向线段lk(k=1，2，…，m)形状如何，都属Sm模型，也称为拓展Sm模型.

本定义意味着Sm模型的有向线段可以是直线、圆弧和任意曲线，如图6所示.

定义4拓展mSm模型.拓展Sm对应的mSm为拓展mSm模型.

磁场积分只依赖线段两端向P点张开的角度，因此拓展Sm模型和拓展mSm模型完全遵守零和定理以及互易定理.

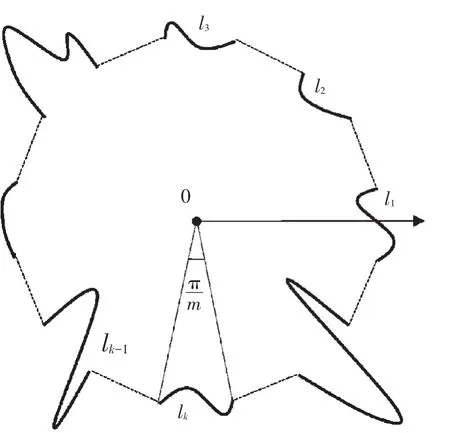
图6 拓展Sm模型

5 结论

1)分析了直通光路型光学电流互感器抗外磁场干扰能力差的根本原因，提出了一种零和御磁技术解决方法.若离散环路外P点的张角之和为零，则离散环路的磁场积分与安培环路定律具有类似形式，这就是离散安培环路定律.

2)研究了正多边离散环路Sm模型和Sm正对称分布的mSm模型，提出了关于离散环路磁场积分的两个重要定理:零和定理和互易定理.零和定理的实质是Sm模型下的离散安培环路定律;互易定理表达mSm模型中所有Sm共同遵守离散安培环路定律之条件.分析结果表明，光学电流互感器按照两个定理设计时，干扰电流产生的磁场可以进入光学电流互感器内部但失去干扰作用.

3)零和定理和互易定理形成了正多边离散环路磁场积分理论体系，是光学电流互感器的零和御磁技术的重要理论基础，为解决直通光路型光学电流互感器的抗外磁场干扰技术难题提供了有益的思路.

［1］Emerging Technologies Working Group.Optic current transducer for power systems:a review［J］.IEEE Transactions on Power Delivery，1994，9(4):1778-1788.

［2］KUCUKSARI S，KARADY G G.Experimental comparison of conventional and optical current transformers［J］.IEEE Transactions on Power Delivery，2010，25(4):2455-2463.

［3］张国庆.光学电流互感器的理论与实用化研究［D］.哈尔滨:哈尔滨工业大学，2005.

［4］于文斌.光学电流互感器光强的温度特性研究［D］.哈尔滨:哈尔滨工业大学，2005.

［5］陈金玲，李红斌，刘延冰，等.一种提高光学电流互感器温度稳定性的新方法［J］.电工技术学报，2009，24(4):97-101.

［6］王佳颖，郭志忠，张国庆，等.光学电流互感器长期运行稳定性的试验研究［J］.电网技术，2012，36(6):37-41.

［7］孙如京，王红星，于文斌，等.自愈光学电流互感器技术及其工程应用［J］.广东电力，2012，25(1):100-104.

［8］冯慈璋.电磁场［M］.北京:高等教育出版社，2011.

［9］NIEWCZAS P，MADDEN W I，MICHIE W C，et al.Magnetic crosstalk compensation for an optical current transducer［J］.IEEE Transactions on Instrumentation and Measurement，2001，50(5):1071-1075.

［10］李红斌，陈庆，刘延冰，等.相间磁干扰对点式光学电流互感器影响的研究［J］.传感器技术，2004，23(4):16-18.

［11］PERCIANTE C D，FERRARI J A.Magnetic crosstalk minimization in optical current sensors［J］.IEEE Transaction son Instrumentation and Measurement，2008，57(10):2304-2308.

［12］路忠峰.御磁技术及其在光学电流传感器中的应用研究［D］.哈尔滨:哈尔滨工业大学，2008.

［13］路忠峰，郭志忠.磁场环路积分的等价解环［J］.哈尔滨工业大学学报，2008，40(11):1781-1784.

［14］于文斌，张国庆，路忠峰，等.光学电流互感器的抗干扰分析［J］.电力系统保护与控制，2012，40(12):8-12.