双路功率分流传动系统的静态均载特性分析

董 皓，方宗德，杜进辅

(1.西北机电工程研究所，712099陕西咸阳;2.西北工业大学机电学院，西安710072)

双路功率分流传动系统采用功率分支技术，结构紧凑，能在很小的体积质量下满足高速重载的工况要求，在航空、航天领域具有广阔的应用前景.功率分流传动系统的核心问题是研究系统的均载特性，解决各分支载荷平均分配，国内外在这方面做了很多研究，Kish［1-2］提出一种应用于Comanche直升机中的双路功率分流齿轮传动减速器.Krantz等［3-4］对双路功率分流减速器的均载问题进行了静力学研究，得出了满足当时制造、安装条件下的均载系数.White［5-6］设计了双路功率分流传动系统中各发动机轴相隔较远且平行布置的方案，得出了该系统重量轻、功率损失小和集成性高的结论.日高照晃等［7］运用静力学方法研究了行星轮系中各个构件的误差对载荷分配系数的影响.方宗德等［8］就三路分流星型减速系统在各级联接刚度和星轮偏心误差影响下的动载荷与均载系数进行了分析.还有一些学者对功率分流做了相关的研究［9-11］，但是，以往研究中大多采用等效平均啮合刚度，并不能完全准确反映真实的齿面啮合过程，本文基于轮齿几何接触分析和承载接触分析将整个啮合过程离散为有限的啮合点，对每个啮合位置进行力学特性分析，可以提高计算的准确性，并且，以往的研究大多仅考虑构件之间的力学平衡关系，而忽略了功率流动闭环的这一特点所构成的变形协调条件，该条件中构件的各类误差会相互叠加或者抵消，所以考虑变形协调条件能够更好地反映整个系统的均载特性.

文中推导出变形协调条件，结合力矩平衡和弹性支承条件，得到系统均载系数，分析了基于花键间隙浮动和径向限位环辅助均载对系统均载特性的影响.

1 系统静力学模型建立

本文针对文献［4］中研究的双路功率分流系统做了理论分析.图1为该系统的结构示意图，该系统应用于某航空直升机动力传输装置.

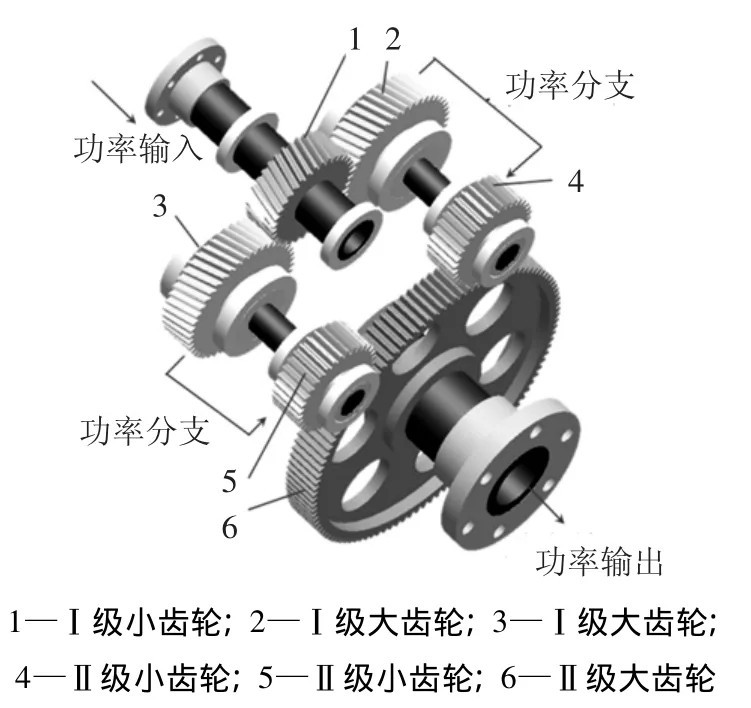
图1 双路功率分流传动系统简图

系统在第Ⅰ级小齿轮采用功率两分支，两级之间通过均载扭力轴传递扭矩，第Ⅱ级两个小齿轮同时与输出大齿轮啮合，各齿轮处靠滚动轴承支承，该系统可进一步提高传动装置功率密度比，有效解决传动装置大扭矩、大速比的要求.力学结构模型和各齿轮转角对应关系如图2所示.

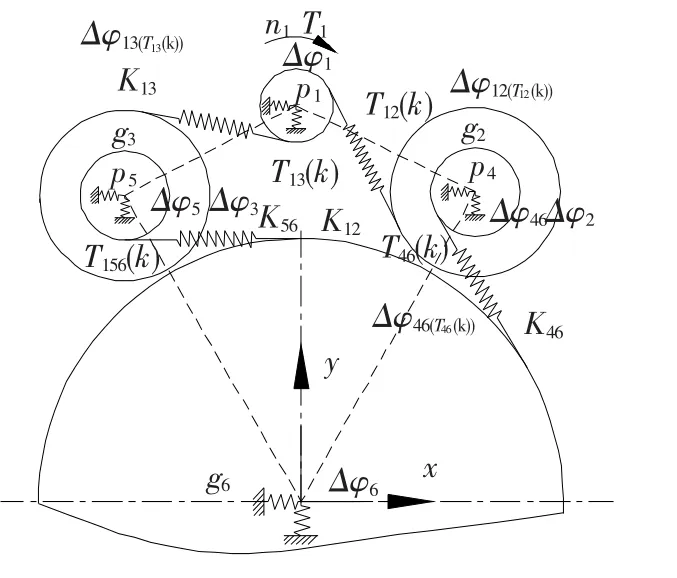
图2 力学结构模型和各齿轮转角对应关系示意图

由图2可知，系统转速为n1，输入扭矩为T1，Kij为时变啮合刚度，Δφi和Δφj为齿轮i、j的扭转角，Δφij(Tij(k))表示齿轮i在扭矩Tij(k)作用下相对于齿轮j的扭转角变形，pu和gv(u=1，4，5;v=2，3，6)表示各齿轮的代号.扭矩相互作用力可表示为Tij=-iijTji(i=1，2，…，6;j=1，2，…，6)，其中iij=rbj/rbi，rbi和rbj为齿轮i，j的基圆半径，得到系统的力矩平衡条件如下:

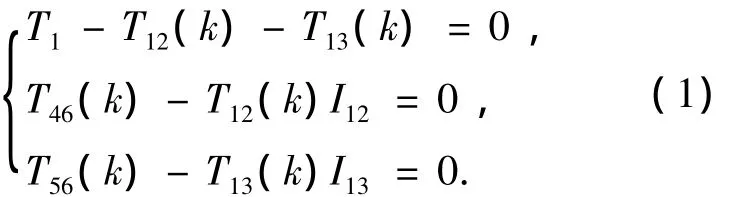
式中:Tij(k)表示齿轮j对齿轮i在一个啮合周期中第k个啮合位置(k=1，2，…，5)的扭矩.

2 系统扭转角变形协调条件

由图2所示的模型，根据系统本身功率流动闭环的特点，功率流动可以分为2个通道，通道1包含齿轮p1、g2、轴24、齿轮p4、g6，通道2包含齿轮p1、g3、轴35、齿轮p5、g6.由于各齿轮副啮合转角满足Δφij(Tij(k))=Δφi-iijΔφj，得到变形协调条件为

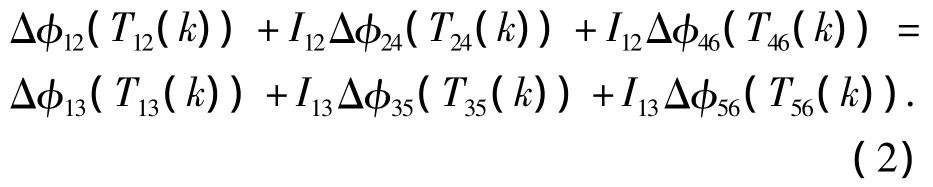
其中，扭力轴的转角关系为

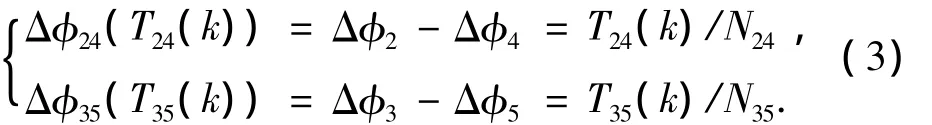
式中:N24和N35为扭转刚度.

误差体现在啮合线上的位移变化ΔLij为

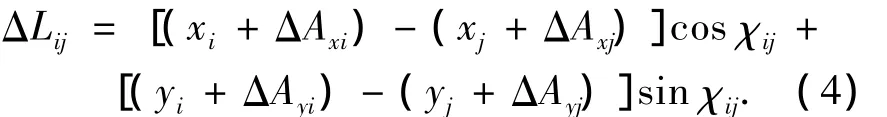
式中:xi、yi和xj、yj分别为齿轮i、j沿x、y向的轴心变形量;ΔAxi、ΔAxj分别为齿轮i、j的x向误差幅值，ΔAyi、ΔAyj分别为齿轮i、j的y向误差幅值;χij为齿轮副啮合线与x轴正向夹角.

啮合作用力可表达为

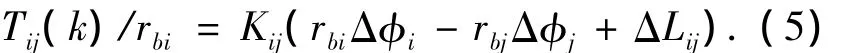
得到误差影响下的各齿轮副啮合转角为

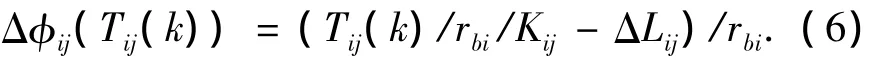
考虑弹性支承条件，可表示为

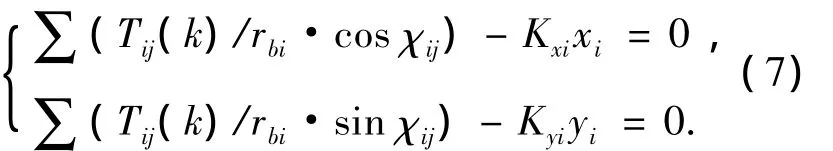
式中:Kxi和Kyi为齿轮i的x、y向的支承刚度.

将式(6)代入式(2)中，得到误差影响下的变形协调条件，联立弹性支承条件和力矩平衡条件，建立系统的弯——扭耦合关系，可求得各齿轮副传递的扭矩Tij，并最终计算得到系统的均载系数，该均载系数的大小表征着系统的均载特性的好坏，均载系数越大，系统的均载特性越差.

3 基于LTCA的时变啮合刚度

轮齿在外载荷作用下啮合时，角变形主要由几何传动误差、弯曲变形和接触变形导致的［11］，这3组引起的扭转角变形和扭矩Tij(k)的函数式描述为

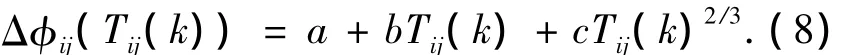
式中:a，b，c为常数项.

忽略轮齿齿面摩擦，假设两对齿(I和II)同时接触.在载荷P作用下，力矩平衡和轮齿接触变形后位移协调条件由下式描述［12］，具体计算可参考文献［12-13］，此处不再赘述.

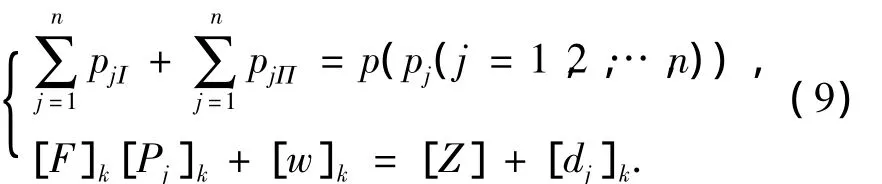
式中:k=Ⅰ，ⅠⅠ，［pj］k=［p1，p2，…，pn］T，［dj］k=［d1，d2，…，dn］T，［Z］=Z［1，1，…，1］T(若pjk＞0，则djk=0;若pjk=0，则djk＞0).pj(j=1，2，…，n)是齿对k的瞬时接触椭圆长轴离散点j处的法向载荷，dj(j=1，2，…，n)是齿对k的瞬时接触椭圆长轴离散点j处变形后的齿面间隙，Z为轮齿的法向位移，［F］k是齿对k的法向柔度矩阵，［w］k为齿面初始间隙，［w］k=［δ］k+［bj］k，bj(j=1，2，…，n)为齿对k的齿面法向间隙，［δ］k=δ［1，1，…，1］T.

对一个啮合周期中所有啮合位置上顺序进行LTCA计算，得到Z、［P］和［d］，Z为当前接触位置载荷P作用下的齿轮变形后的法向线位移传动误差，将其变换为角位移误差Δφij［12-13］.

通过计算某一啮合位置k下不同载荷作用下对应的多组承载传动误差，将其分别带入式(9)，即可确定系数a，b，c，同时，可以推导出承载传动误差与名义载荷的函数关系式，再拟合出一个啮合周期中各啮合位置下承载传动误差随扭矩Tij(k)变化的函数关系式，最后得到各对齿轮副时变啮合刚度，可表示为

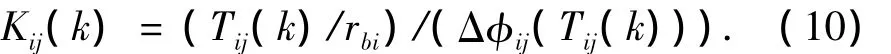
该刚度能够更加直接的反映出齿轮在各啮合位置的啮合特性.

4 花键间隙浮动条件

第Ⅰ级小齿轮做成浮动结构，与高速输入轴和输出件用可活动的短花键联接，由花键传递扭矩.浮动轮受花键联接的约束，不能完全自由浮动，浮动轮的支承刚度如图3所示.

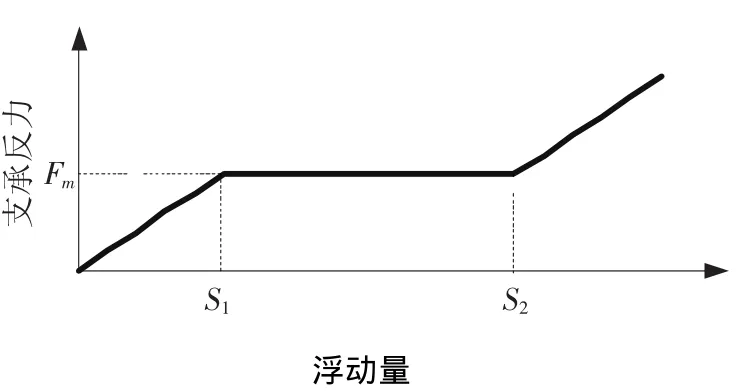
图3 浮动轮支承刚度示意图

由图3示出，在花键传递扭矩的过程中，内外花键摩擦力为Fm=τFN，FN表示内外花键之间的正压力，τ为摩擦系数，取τ=0.1.浮动时的浮动量为表示在x和y方向的浮动量，n代表计算次数.

浮动过程中，浮动小轮受到2个啮合大齿轮的啮合力和花键联接轴的支承反力共同作用，当支承反力小于摩擦力Fm时，内外花键之间不产生滑移，由输入轴的弯曲适应小轮位置变化，即0～S1段;当支承反力大于摩擦力Fm时，内外花键产生滑移，由滑移量适应浮动轮的位置变化，即S1～S2段;当滑移量超出S2时，即内外花键消除了径向间隙量，小轮位置变化重新由输入轴的弯曲变形决定，图3中S1～S2即为内外花键的径向间隙.浮动小轮支承反力在x、y向的分量ΔF(

x1n)、分别为

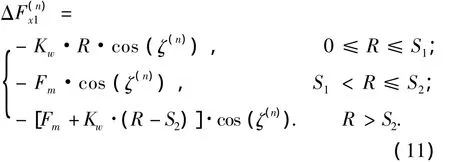
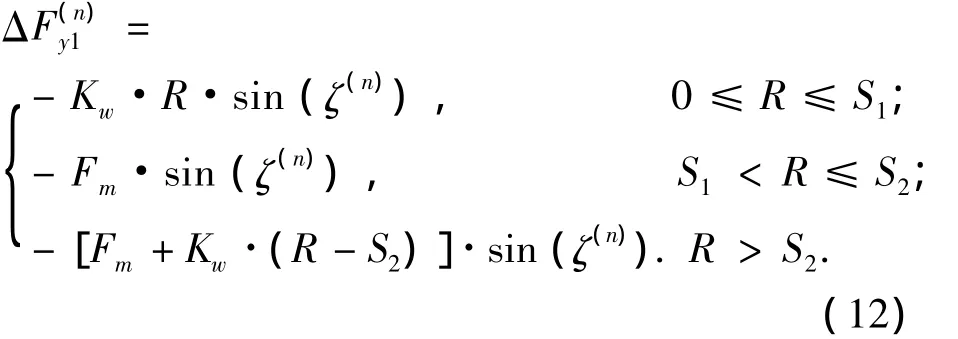
式中:Kw表示弯曲刚度，ζ(n)表示向量的方向角.则有，浮动件的支承平衡条件:

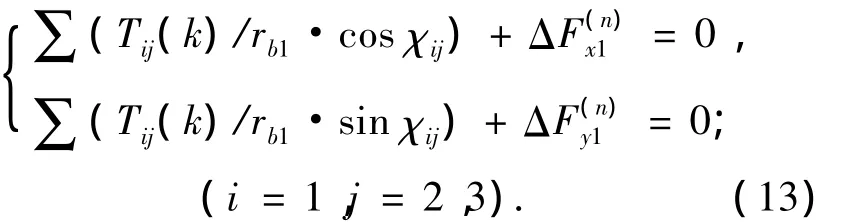
将式(14)联立其它各构件的支承平衡条件和力矩平衡条件以及变形协调条件，建立间隙非线性数学模型，可以求解得到系统的均载系数.

5 径向限位环辅助均载条件

浮动件在浮动过程中，没有径向支承，为了防止浮动量过大而脱离啮合状态，则浮动轮的两端面上分别设有一个径向限位环，径向限位环起辅助均载的作用.浮动轮径向限位环的外径与浮动轮的节圆直径相等，两个关联的大齿轮的径向限位环的外径与大齿轮的节圆直径相等，如图4所示.

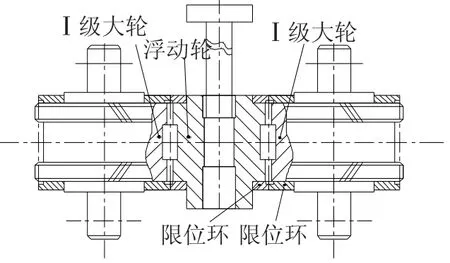
图4 限位环结构示意图

同时，应保证浮动轮和其关联的齿轮同步运动，形成封闭力系，如图5所示.

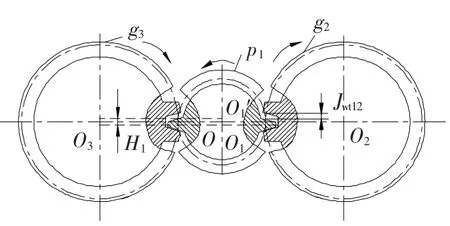
图5 浮动轮相互运动关系示意图

浮动轮的中心可在O1～O1'之间上下浮动来满足均载，左右摆动由两侧大齿轮空刀槽里的径向限位环限制.当浮动轮与齿轮3啮合时，受到齿轮啮合力的作用，浮动轮中心有向上运动的趋势，以消除浮动轮与齿轮2间的圆周侧隙jwt12，此时浮动轮的中心O向上浮动到O1'的位置.浮动轮与齿轮2啮合时，向下浮动同理.浮动区域如图5中H1所示，如果浮动平衡点超出该区域内，则将浮动轮的平衡位置点强行定位在径向限位环的边界上，此时，径向限位环起支承作用.浮动轮在两个相互啮合的齿轮和径向限位环的支承反力的共同作用下自动定心，得到平衡条件如下:

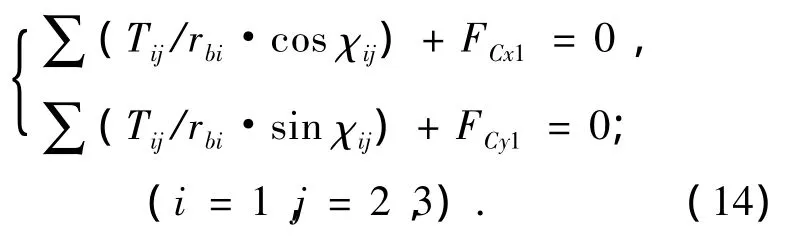
式中:FCx1和FCy1为限位环在x和y向的对浮动轮的支承反力.

6 算例求解

算例中各参数完全依据文献［4］中的实验参数，功率373Kw，转速8 780 r/min，数据见表1.

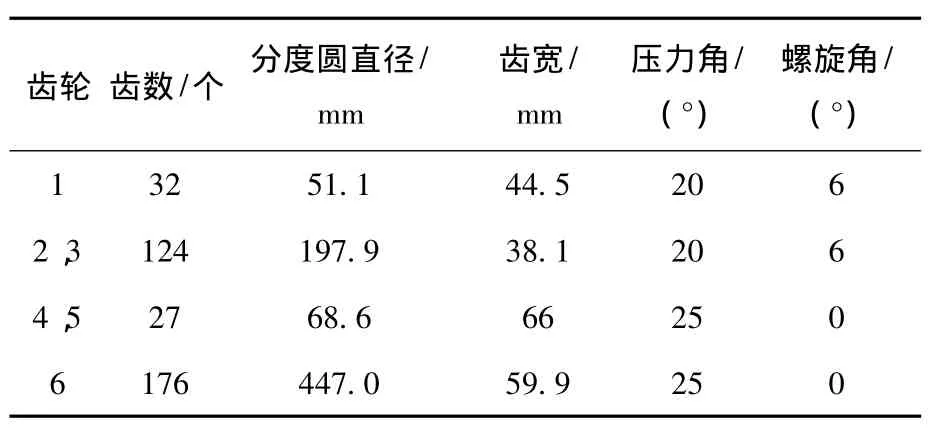
表1 各齿轮参数

根据第3小节所述的方法，计算得到两级各齿轮副的啮合刚度如图6所示.

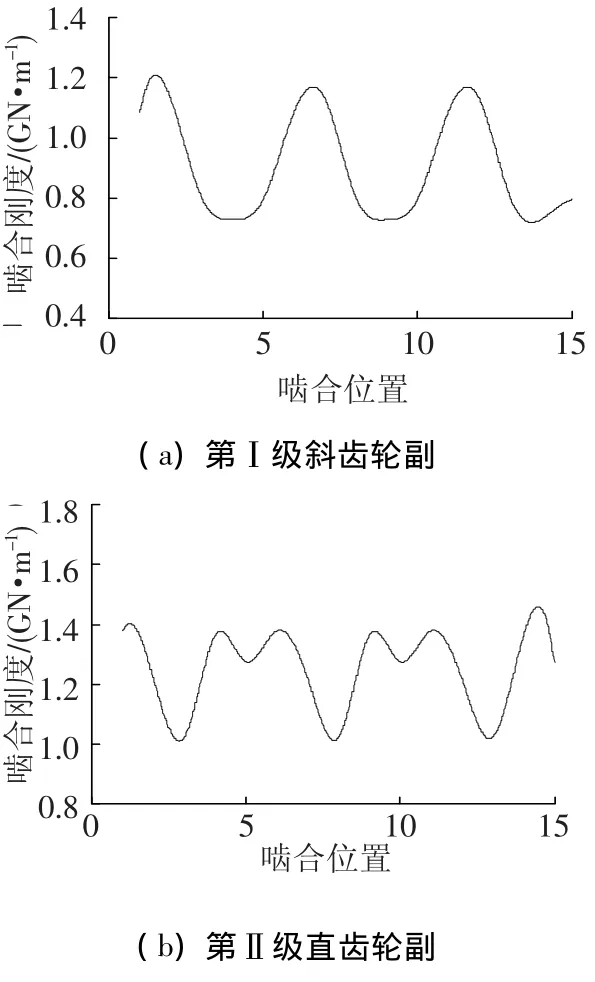
图6 时变啮合刚度曲线图

各轴承数据引用文献［4］中的tableⅡ的轴承数据，轴承刚度计算按照GB/T307.3—1996计算.

取ΔAx2=ΔAx4=ΔAx6=0.05 mm，当安装误差共同作用时，计算得系统的均载系数为1.089 3，功率分配为54.47%.各个误差分别作用时的扭矩分配如图7所示.可以看出，扭矩在各个啮合位置成周期性波动，反应了齿面上不同啮合位置点的载荷分配.ΔAx2、ΔAx4和ΔAx6影响下的均载系数分别为1.020 7、1.078 3和1.064 1，功率分配为51.03%、53.92%和53.21%.且误差具有累加作用.

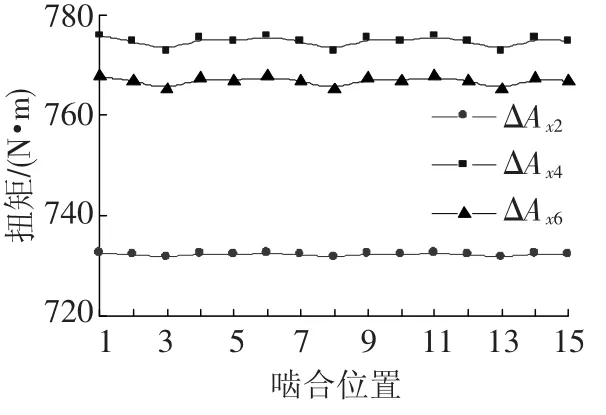
图7 安装误差影响下的扭矩分配

误差ΔAxi(i=2，4，6)单独变化时，均载特性如图8所示.可以看出，均载系数随安装误差的增大而增大，第Ⅱ级小齿轮影响最大，其次是第Ⅱ级大齿轮，最后是第Ⅰ级大齿轮.

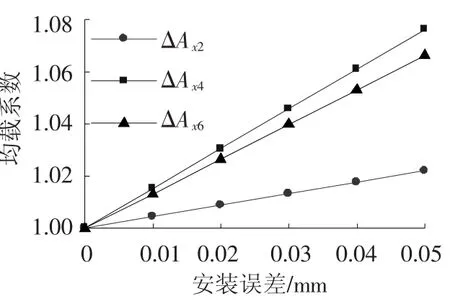
图8 安装误差单独变化时系统的均载系数曲线图

均载系数随花键间隙量变化的情况如图9所示，给定ΔAx2=0.05 mm，ΔAx4=0.05 mm，τ=0.1.可以看出，间隙越大，均载特性越好，花键间隙量为0时，完全由轴的弯曲适应浮动轮的位置变化.由于摩擦力的影响，最后在不同误差下得到均载系数分别为1.004 2和1.007 9.

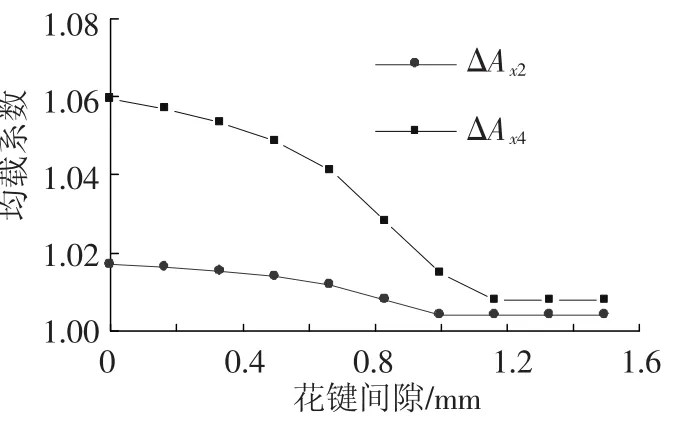
图9 均载系数随间隙量变化曲线图

当花键间隙量满足浮动轮完全浮动时，浮动轮要受到在限位环的径向限位，图10给出了均载系数随侧隙量变化的情况，给定误差为ΔAy2=0.05 mm和ΔAy4=0.05 mm.可以看出，在误差恒定的条件下，侧隙量越大均载性能越好.侧隙量为0时，浮动轮则相当于轴承支承，得到均载系数分别为1.015 1和1.056 3，当侧隙量足够大时，系统达到完全理想的均载特性.

图11给出了浮动轮平衡位置点的中心轨迹.可以看出，在径向限位环的作用下，不同误差影响下，浮动轮最终达到平衡位置，平衡点为(-2.978 1×10-7，0.018 3)和(-4.833 8×10-6，0.073 6)，且落在径向限位环边界上.

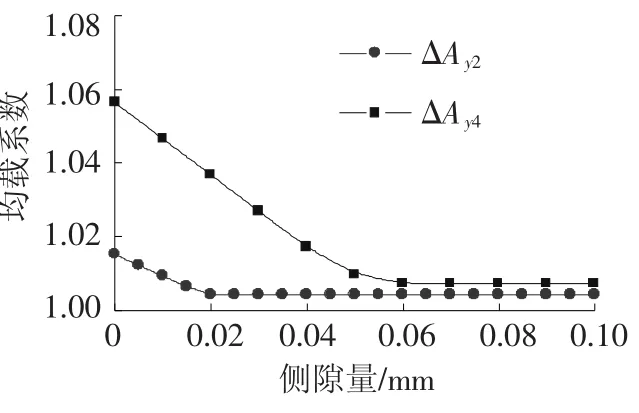
图10 均载系数随间隙量变化曲线图

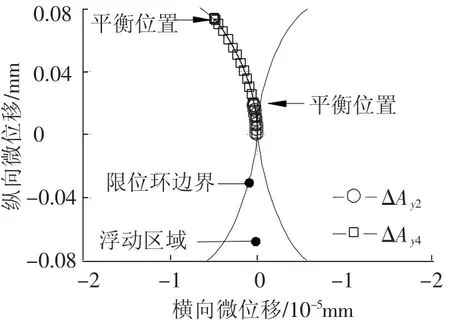
图11 浮动轮中心位置浮动轨迹

7 数据分析和实验

由文献［4］所述，2路分支在传递扭矩过程中存在一个使得系统的均载特性发生变化的夹角β，该夹角可以通过图12所示的方式测量.

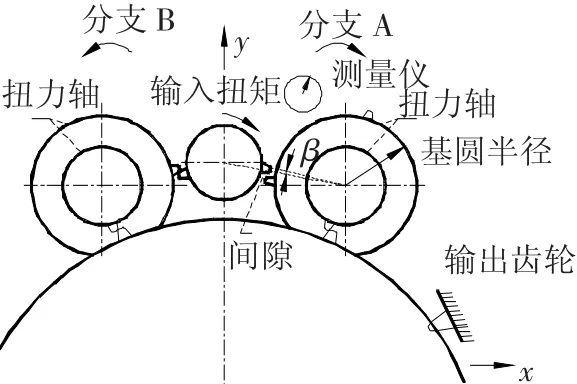
图12 测量扭转夹角β的实验示意图

实验中通过在第Ⅰ级大齿轮轴向增加薄垫片的方法来改变该夹角β，由图12示出，首先测量了不同薄垫片厚度下输入扭矩和扭力轴传递的扭矩的关系，同时测量了薄垫片的厚度和夹角β之间的函数关系，从而建立了给定某一特定输入扭矩时扭力轴传递的扭矩和夹角β的函数关系，最后确定某一夹角β以使扭力轴传递的扭矩能够满足功率分配在50%±3%范围内.

实验中给定薄垫片厚度为3 mm时，扭力轴传递扭矩随系统输入扭矩变化的关系如图13(a)，同时给出理论计算结果如图13(b)所示.

由图13(a)可知，实验数据的一侧分支扭矩为728.61 Nm，另一侧分支扭矩为625.32 Nm，则功率分配为53.88%，均载系数为1.077 6，由图13(b)可知，理论分析数据的连接轴的一侧分支扭矩760.89 Nm，另一侧分支扭矩661.23 Nm，得到功率分配为53.50%，均载系数为1.070 1.理论和实验结果对比，趋势一致，验证了本文方法的正确性和可行性.

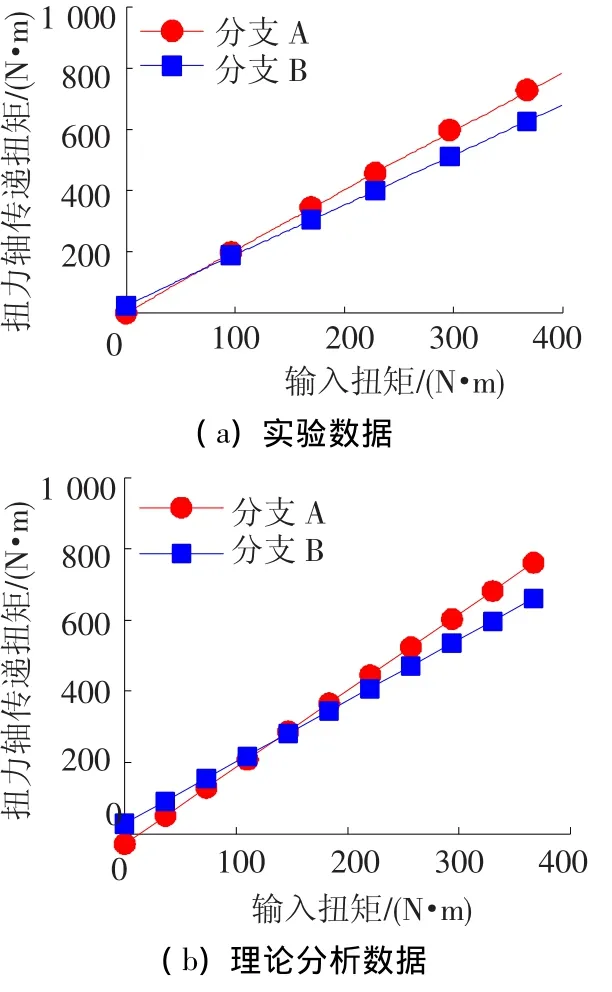
图13 实验数据和理论分析数据对比曲线图

8 结论

1)同一误差下各构件对系统均载系数的影响不一样，尤其应注意第Ⅱ级构件的误差分布情况.

2)间隙浮动能提高系统的均载特性，设计时花键的最小间隙量可取为各误差引起的浮动件的最大极限位移量，就可满足均载浮动的要求.

3)径向限位环起到了良好的辅助均载作用.

通过实验验证了本文方法的可行性和正确性.

［1］KISH J G.Sikorsky aircraft advanced rotorcraft transmission(art)program-final report［R］.Cleveland:NASA Lewis Research Center，NASA CR-191079，1993.

［2］KISH J G.Comanche drive system［R］.Williamsburg:Rotary Wing Propulsion Specialists’Meeting:Proceedings，American Helicopter Society，1993.

［3］KRANTZ T L，A method to analyze and optimize load sharing of split path transmission［R］.Cleveland:NASA Lewis Research Center，NASA TM-107201，1996.

［4］KRANTZ T L，DELGADO I R.Experimental study of split-path transmission load sharing［R］.Cleveland:NASA Lewis Research Center，NASA TM-107212，1996.

［5］WHITE G.Split torque helicopter transmissions with widely separated engines［J］.Proceedings of the Institution of Mechanical Engineers，Part G:Journal of Aerospace Engineering，1989，203(1):53-65.

［6］WHITE G.Design study of a split-torque helicopter transmission［J］.Proceedings of the Institution of Mechanical Engineers，Part G:Journal of Aerospace Engineering，1998，212(2):117-123.

［7］日高照晃，衫本信行，石田武.遊星歯車装置の荷重等配機構における各種誤差と荷重配分の関係［C］//日本機械学会論文集.東京:日本機械学会，1986，52(480):2200-2206.

［8］方宗德，沈允文，黄镇东.三路功率分流恒星式减速器的动态特性［J］.航空学报，1990，17(7):341-350.

［9］张婷，李育锡，王三民.功率二分支齿轮传动系统静态均载特性研究［J］.机械传动，2012，36(3):14-24.

［10］杜进辅，方宗德，王宝宾，董皓.基于变形协调的行星轮系均载特性研究［J］.航空动力学报，2012，27(5):1166-1171.

［11］谷建功，方宗德，庞 辉，王成.弧齿锥齿轮功率分流传动系统建模与承载特性分析［J］.航空动力学报，2009，24(11):2625-2630.

［12］方宗德.修形斜齿轮的承载接触分析［J］.航空动力学报，1997，12(3):251-254，329.

［13］LITVIN F L.Gear geometry and applied Theory［M］.New Jersey:PTR Prentice Hall，1994:258-280.