改进Kriging模型在固冲发动机导弹气动优化设计中的应用①

杨 军，刘勇琼，艾春安，张 菲

(1.第二炮兵工程大学，西安 710025;2.中国航天科技集团公司四院四十三所，西安 710025;3.中国航天科技集团公司四院四十一所，西安 710025)

0 引言

导弹气动问题具有高度非线性，且受限于CFD计算效率。因此，在其气动优化设计研究中，无论是基于梯度信息的直接优化法，还是遗传算法等现代智能非梯度优化方法，算法的收敛难度和速度均不满足工程实际需要［1］。

近似优化技术本质上将便于计算的近似函数耦合到优化算法中，代替复杂的学科分析进程，多次迭代循环后，得到实际问题的近似最优解。Kriging模型由于适用于拟合高度非线性、多峰值的问题而广泛用于飞行器气动优化设计中。Shinkyu J等［2］将Kriging模型和遗传算法相结合，对二维翼型进行了优化设计。张科施等［3］将Kriging模型和其他近似模型进行比较后，建立了基于近似技术的多学科设计优化框架，并用于高亚声速运输机机翼气动/结构优化设计。许瑞飞等［1］将超立方抽样试验设计方法、EI方法、不断更新的Kriging模型与优化方法结合，发展了基于改进Kriging模型的优化设计算法，并用于RAE2822翼型优化设计中。孙美建等［4］采用改进的量子粒子群算法，对Kriging模型的相关参数进行优化，并与具有双层结构的粒子群算法相结合，对高维度、多目标、多约束的跨声速机翼进行了优化。目前，国内还没有将Kriging模型用于冲压发动机导弹气动优化设计中，且对该近似模型的拟合精度研究也不够深入。

本文在深入研究相关参数θ对导弹气动学科Kriging近似模型拟合精度影响的基础上，基于最优相关参数将均匀试验设计方法、Kriging模型与遗传算法结合，提出了一种基于改进Kriging模型优化设计框架。将该方法用于固冲发动机导弹气动优化设计中，优化后导弹的升阻比得到了极大提高，表明本文方法是可行的。

1 Kriging模型

Kriging模型中响应值与设计变量之间的关系可表示为

式中 y(x)为未知函数;f(x)为设计空间的全局模拟;z(x)为局部偏差。

式中 pT(x)为多项式基函数组;β为系数向量。

z(x)为随机过程的实现，其统计特性为

式中 R为相关矩阵;R(xi，xj)是任意两样本点xi、xj的相关函数。

R是n×n阶对称矩阵(n为样本点个数)，相关函数的形式常用的有指数函数、高斯函数、样条函数等，本文选取的高斯相关函数表达式为

式中 ndv为设计变量个数;θk为未知的相关参数;xik、xjk是样本点 xi、xj的第 k维元素。

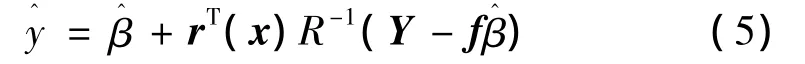
式中 Y为样本点响应量矩阵;f为全1列向量;r(x)为样本点和预测点之间的相关向量。

r(x)满足:

方差由式(8)求得:

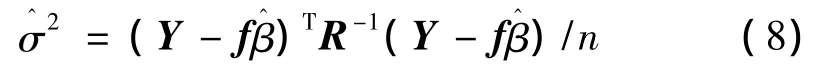
式(4)中的相关参数θk可由极大似然估计得到:

任意一组θk都能生成一个插值模型，但最优的θk能使得Kriging模型的预测精度最高，这需要求解式(9)的无约束非线性优化问题得到。

2 基于遗传算法的最优相关参数

2.1 问题分析

本文基准导弹方案采用整体式固冲发动机、双下侧二元进气道，2个弹翼和4个操纵尾翼呈X-X型正常式气动布局。其典型纵向弹道可分为爬升段、巡航段和俯冲段。导弹巡航马赫数为3，巡航高度10 km。根据不同外形参数对导弹气动力系数的不同程度的影响，本文选取下述7个变量作为导弹气动优化设计变量:导弹头部长细比λn、弹翼展弦比λw、弹翼梢根比ηw、尾翼梢根比 ηT、弹翼后掠角 χw、尾翼后掠角 χT、进气道唇口宽高比kn，各变量的取值范围如表1所示。

2.2 遗传算法(GA)求解

在Matlab下开发遗传搜索算法源程序，求解导弹气动优化问题的最优相关参数θ。同样，用上述的21组数据作为构造Kriging模型的初始样本点。遗传算法主要参数:θ取值空间为［0，15］，初始种群规模为100，最大进化代数40。源程序模块包括GA主程序、适应值函数计算模块、优化结果输出模块。程序独立运行10次，每一次均收敛良好且结果统一。图2为升阻力系数最优相关参数θ的GA迭代收敛曲线。

表1 优化变量取值范围Table 1 Range of the optimization variables

图1 Kriging近似模型相关系数曲线Fig.1 The correlated parameters of Kriging approximate model

图2 相关参数GA优化迭代历史Fig.2 Correlated parameter＇s iterative history of GA

由上述结果可知，升力系数相关参数θ稳定收敛到最优解3.08，阻力系数相关参数收敛到最优解12.002，即对于本文的导弹气动学科 Kriging近似模型，在上述21组初始样本点数据基础上，最优的相关参数 θ分别取3.08、12.002。

2.3 Kriging近似模型精度预测

为了验证在最优θ取值条件下，Kriging近似模型对导弹气动特性的预测能力，这里对气动问题的拟合能力做了进一步检验。在随机产生的20组预测样本点条件下，分别用所建立的Kriging近似模型和Missile datcom精确分析模型计算导弹的气动力系数，2种模型下升力系数、阻力系数比较如图3所示，对应的该近似模型精度如表2所示，其中，e－为相对误差均值，σe为相对误差标准差，二者的具体定义可参考文献［5］。

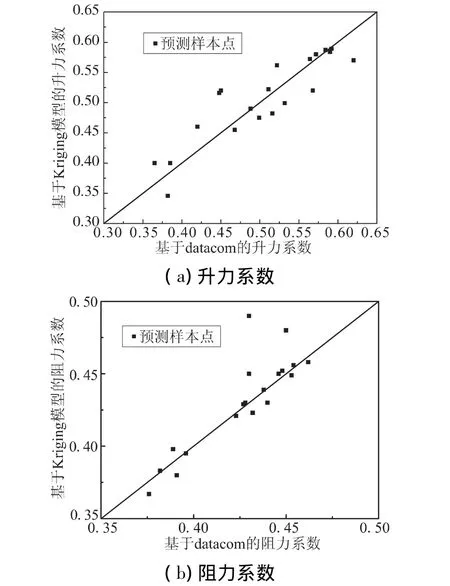
图3 预测样本点处气动力系数比较Fig.3 Comparson of aerodynamic coefficients on predicted sample points

表2 预测样本点处Kriging近似模型精度评估Table 2 Accuracy of Kriging approximate model on predicted sample points

综上结果可见，尽管初始样本点较少，但本文构造的用于固冲发动机导弹气动优化的Kriging近似模型精度满足要求，该模型能够在一定精度范围内替代比较耗时的气动分析程序，并完成相关的气动优化设计工作。

3 导弹气动优化设计

3.1 基于改进的Kriging模型优化设计算法框架

本文在遗传算法每次迭代中，都将上一代的最优个体信息加入到原有样本集中，然后重新生成Kriging模型，这样样本点数量将随着优化迭代不断增加并更新，同时不断接近最优解的临域。图4为基于不断更新的Kriging模型的优化设计算法框架。

图4 基于Kriging模型的优化设计算法框架Fig.4 Improved algorithmic framework based on Kriging approximate model

3.2 固冲发动机导弹气动优化设计

根据图4算法框架进行导弹气动优化设计，采用遗传算法寻找目标函数的最优值。以弹翼和尾翼面积作为约束条件，弹身最大横截面面积保持不变，进行全弹最大升阻比优化设计。导弹飞行工况取巡航状态:攻角2°，马赫数 3.0，雷诺数 Re=5 172 612.76，优化问题可描述为

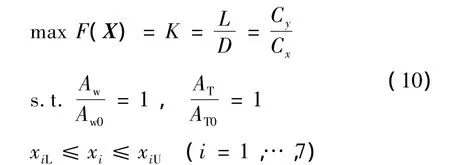
式中 K为升阻比;AW、AT分别为弹翼和尾翼面积;AW0、AT0分别为优化前导弹弹翼和尾翼面积;xiL和 xiU分别为设计变量取值上下限。

控制遗传算法最大进化代数100，初始种群规模取300，GA迭代历史如图5所示。表3给出了优化前后导弹各气动外形参数(即各设计变量)和升力系数、阻力系数、升阻比(即状态变量)相对于原基准值的变化。

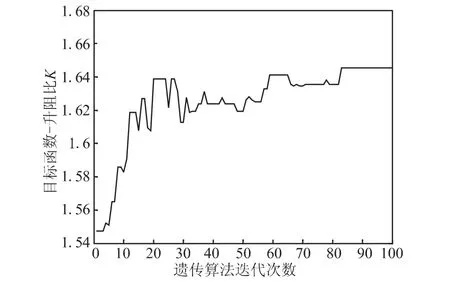
图5 遗传算法气动优化迭代历史Fig.5 Optimized iterative history of GA

表3 导弹气动优化设计结果Table 3 Results of aerodynamic optimization

由上述结果可见，本文采用的气动优化算法稳定收敛。优化后弹翼和尾翼横截面形状均变化明显，弹翼后缘掠角明显增加，尾翼前后缘掠角均有很大增加，但梢根比有减小。另外，导弹头部更加细长，这对减阻和气动防热设计均有利，进气道本身相当于一个升力面，其入口宽高比也有增加。优化设计最终得到的方案下，全弹阻力系数下降了13.9%，而升力系数上升了4.92%，最终的升阻比上升达21.9%，且优化前后导弹弹翼、尾翼面积保持不变，优化设计的结果较好。

另外，随着遗传算法迭代次数的增加，越来越多的样本点被加入到样本集中，Kriging模型的近似精度也得到很大提高。同时，针对在最优解附近可能有多个相近峰值，GA求解获得的最优群体一般分布于各个峰值附近，以上算法通过多次更新Kriging模型，也可避免漏选全局最优解。

4 结束语

(1)本文通过求解最优相关参数，对Kriging模型的拟合精度进行了详细研究。结果表明，在样本点个数受限条件下，通过搜索算法求得最优相关参数，可保证Kriging模型具有足够的拟合精度。

(2)提出一种基于不断更新Kriging模型的优化设计算法框架，并用于固冲发动机导弹气动优化设计研究中，实现了导弹气动性能的较大提高，对实际工程设计具有指导意义。

［1］许瑞飞，宋文萍，韩忠华.改进Kriging模型在翼型气动优化设计中的应用研究［J］.西北工业大学学报，2010，28(4):503-510.

［2］Shinkyu J M M，K Y.Efficient optimization design method using Kriging［R］.AIAA 2004-118.

［3］张科施，韩忠华，李为吉，等.基于近似技术的高亚声速运输机机翼气动/结构优化设计［J］.航空学报，2006，27(5):810-815.

［4］孙美建，詹浩.Kriging模型在机翼气动外形优化中的应用［J］.航空动力学学报，2011，29(6):759-764.

［5］于剑桥，文仲辉，梅跃松，等.战术导弹总体设计［M］.北京:北京航空航天大学出版社.2010.