工程项目估价概率分析
周建国,徐宁,杨正凯
(1.山东建筑大学 管理工程学院,山东 济南 250101;2.山东建筑大学 理学院,山东 济南 250101;3.山东建筑大学土木工程学院,山东 济南 250101)
0 引言
在项目策划及实施的各个阶段,都要进行工程估价。现行的工程估价方法是根据建筑产品在建造过程中所发生的费用,以施工过程为依据,计算工程数量及单价,或套用定额(估算、概算、预算定额),按照取费标准计算得到的是一个固定值。建筑产品在生产过程中受各种因素的影响,如企业劳动生产率的高低、原材料的消耗量及价格变动、机械设备的利用程度、项目管理水平、以及现场条件的变化和工程合同条款的不同、市场竞争程度等[1]。由于这些不可控因素的影响,在预计工期内,工程项目有些费用是随机的,存在着多种变化状态(或范围),很难精确的进行估算[2-3]。准确的工程估价,对项目发起组织和设计团队都是非常重要的[4-6]。不准确的估价,必然会增加项目的风险[7-8]。国内外概率的应用研究主要集中在工程的评价、决策、极限状态评估等领域,如风险(安全)评价、计划评审技术PERT(Program Evaluation and Review Technique)及可靠性评估等方面,而应用在工程估价方面,尚缺少系统的研究。文章拟将概率分析的概念引入到工程估价中,验证单项工程估价偏差或误差分布近似服从β分布,单项估价的累加平均值近似服从正态分布,可以应用中心极限定理为项目估价给出一个概率范围,从而为项目的决策和风险评估提供有价值的信息。
1 工程项目估价原理及程序
1.1 项目估价值概率分布的确定
建设工程项目的计价是一个复杂过程,其基于通用的环境和条件、正常的执行情况。因为确定项目估值的因素,如材料设备的价格,工资、利率、汇率等是不断变化的,这些变化影响了建设工程费用估价的准确性,将这些影响定义为偏差或误差,这些偏差或误差决定了项目估价的不确定性[8-10]。
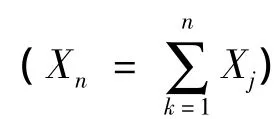
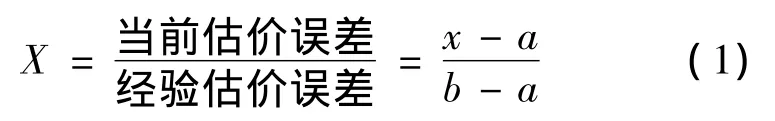
式中:x为当前估价;a为经验估价最小值;b为经验估价最大值。
则X具有下列三个特征:(1)X在0,1之间;(2)X的取值具有随机性;(3)X与1-X在几何上具有对称性。具有这些特征的随机变量可看作服从或近似服从β分布。即X的密度函数如下
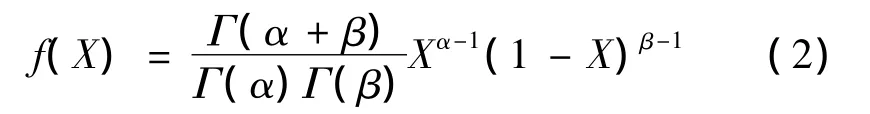
通过β分布计算随机变量的均值和方差十分方便。估算出随机变量X的均值后,我们可推出当前估价x的均值与方差。
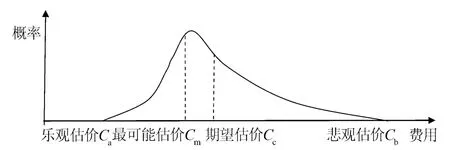
图1 β分布曲线
假设分项工程x有一个有限的乐观估价x1、悲观估价x2以及最可能估价xm,则对应相对误差有乐观误差x1、悲观误差x2和最大可能误差xm。这三个值是主观估计值,根据它们可推算出相对误差X的均值与方差,并推算出估价X的均值(μX)与方差(σ2)。

注意:当a≤x1≤b、a≤x2≤b时,经常地用a、b 分别表示 x1、x2。
1.2 项目估价概率分布规律分析
工程项目的估价是由大量的项目活动发生的费用累加得出的,其中每一个项目活动费用在总费用中所起的作用都是微小的,没有一项因素起特别突出的影响,项目的总费用受多个随机因素的影响,这种随机变量往往近似地服从正态分布。在项目费用的确定过程中,我们往往只关心项目的总费用,而不关心个别因素的作用,为了评估项目费用的不确定性,可以用中心极限定理来描述随机变量和的概率分布规律,即在一般情况下,大量随机变量的平均值近似服从正态分布[11],因此可以应用正态分布对项目费用发生情况作近似分析。
假设某项目要进行投资决策,共有n个分项项目,构成随机变量序列C1,C2,…Cn其相互独立,服从同一分布,由上一步分析知:

注意到等式(7)的右端是标准正态分布的分布函数。即当n充分大时(n>15),独立同一分布的n个随机变量C1,C2,…Cn之和近似地服从正态分布 N(nμ,nσ2)。
1.3 项目估价概率分析计算程序
1.3.1 根据已知计划费用确定项目可完成的概率
(1)确定估价项目,并对每一项目进行乐观、悲观和最可能性估价分析。
(2)求每一估价项目的均值和方差。即求出
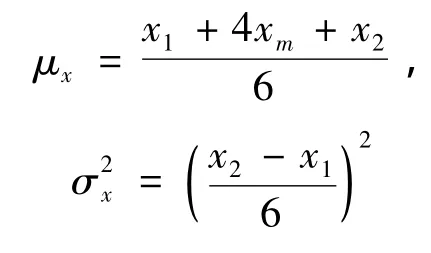
(3)确定项目总费用值的均值。
(4)计算项目费用的标准偏差:
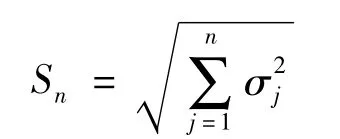
(5)用标准偏差确定标准正态曲线的横坐标值Z,即
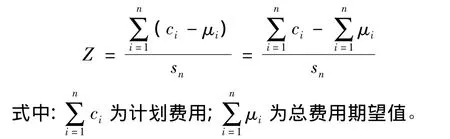
1.3.2 根据项目费用控制要求的控制可靠性概率,确定期望费用
用上例相似的方法,根据已知概率可求出期望费用。
2 工程项目估价概率实例分析
某大型国际机场项目,计划投资额为89.4亿元,建设方在投资决策前,需要做一个针对项目投资合理性的经济分析,确定能够按此投资额完成建设的把握。
(1)确定估价项目并进行三值估计
根据项目设计,项目共由86项估价项目组成,为了得到项目按计划投资额完成的概率,成立了一个由多位估价专家组成的专家组,为项目活动给出了乐观、悲观及最可能投资估计值(如表1所示)。
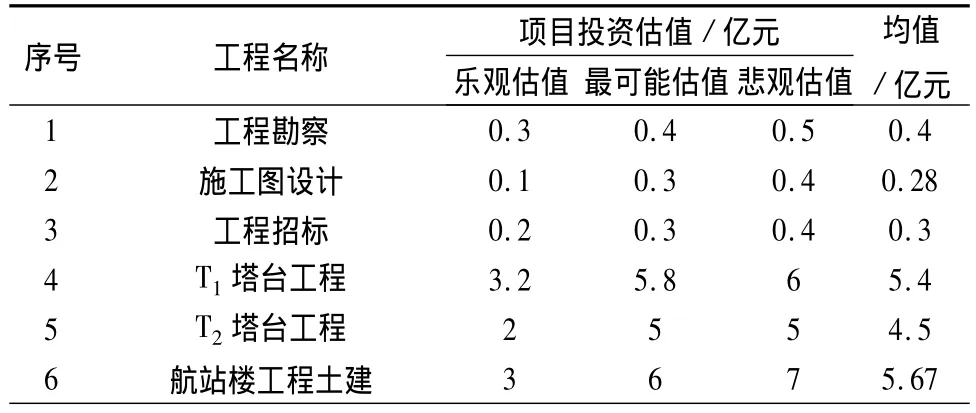
表1 项目估值表
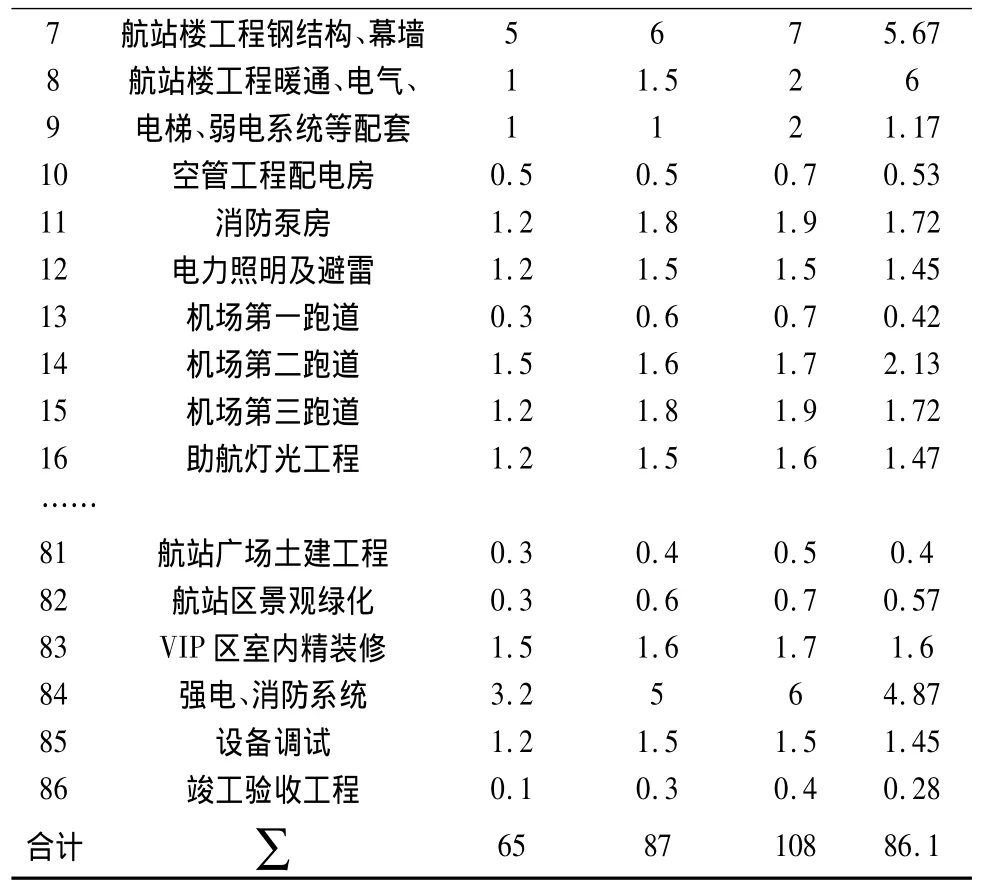
续表1:
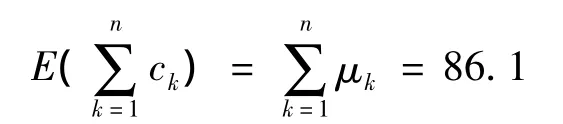
(3)计算项目估值方差及正态分布的标准偏差
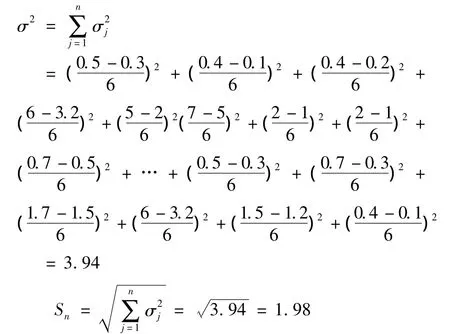
(2)确定工程投资的总平均估值
由公式(3)及表1确定工程投资的总平均估值
(4)用标准差确定正态曲线横坐标值
(5)确定项目期望投资额完成概率

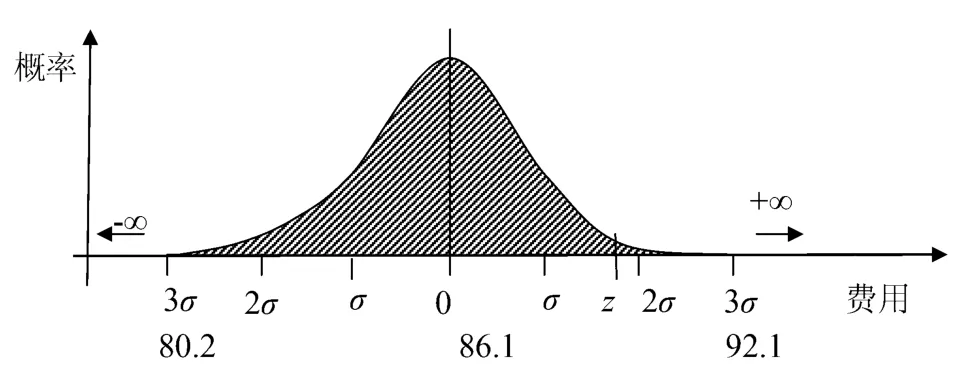
图2 正态分布曲线
即有95%的置信度,保证工程在计划投资额89.4亿元内完成。
3 结论
工程项目的建设是一个复杂和有较长建设周期的过程,在项目建设的不同阶段需要做出相应的项目估算(设计概算、施工图预算及竣工结算等),估算的精度取决于项目已知的信息量,估算的误差最大可能会达到+50%到-30%的范围。研究将概率分析的方法应用到工程估价中,验证了(1)每一项工程的估价都是大量随机变量的叠加,这些随机变量的平均值近似服从正态分布,可以应用中心极限定理来描述其分布规律;(2)应用概率分析做出的项目估价,可以给出估价值的置信度及置信区间或估价值的浮动范围;(3)此估价方法在估价项目数量较大(>15)时结论才为有效。
[1]陈建国.工程计量与造价管理[M].上海:同济大学出版社,2001.
[2]陈胜群.现代成本管理理论[M].北京:中国人民大学出版社,1998.
[3]王槐林.采购管理与库存控制[M].北京:中国物资出版社,2012.
[4]邢莉燕,邵朝红.云视角下的工程造价风险评价[J].山东建筑大学学报,2010,25(4):429 -433.
[5]邓培林,袁建新.基于招投标博弈报价策略分析[J].数学的实践与认识,2011(12):78-80.
[6]邢亚倩.基于资金时间价值的投标决策过程的资源优化[J].西南交通大学学报,2012(6):45-47.
[7]徐立新,张新成,吴相林.基于数理统计的工程投标决策定量分析方法及应用[J].计算机工程与应用,2006(08):46-47.
[8]Ellram L.M.A..Managerial guideline for the development and implementation of purchasing partnerships[J].Intemational Joumal of Purchasing and Materials Management,1991,27(3):2 -8.
[9]Landeros R.R.,Plank R.E..Maintaining buyer supplier patner ships[J].International Goumal of Purchasing and Materials Management,1990,31(3):3 -31.
[10]王雪青,张帆.基于DEA-Tobit的建筑业企业效率研究[J].山东建筑大学学报,2011,26(4):343 -347.
[11]杨永发.概率论与数理统计教程[M].天津:南开大学出版社,2000.
[12]赵道致,张文慧.招投标中的激励机制设计[J].现代财经-天津财经学院学报,2002(11):28-30.

