蓖麻籽冷榨塑性模型试验研究
黄志辉 ,施亮林 ,李昌珠 ,肖志红 ,程鑫鑫,刘汝宽
(1 中南大学 机电工程学院,湖南 长沙 410083;2 湖南省林业科学院,湖南 长沙 410004)
蓖麻是世界十大油料之一,被广泛应用于润滑剂、医药等领域.螺旋压榨是从植物油料中提取油脂最广泛采用的一种方法[1-2].目前国内外有关学者在常见油料(如菜籽、大豆)压榨机理方面取得了一些研究成果.郑晓等[3-4]运用川北方程推导出了蓖麻籽临界压榨压力,但没有给出蓖麻籽塑性模型.张亚新等[5]建立的基于Kuhn 准则的葵花籽塑性模型,对于葵花籽而言还存在较大的误差;赵东等[6]利用Doraivelu 屈服准则建立了玉米秸秆压缩时的塑性模型,并不适用于蓖麻籽;Bargale 等[7]研究了大豆出油和压榨时间的关系,而未对大豆的塑性模型进行研究.有关蓖麻籽压榨过程中的力学模型研究鲜见报道.实际生产发现,蓖麻籽出油主要集中在蓖麻籽壳体破裂后的塑性阶段,为了认识其在塑性阶段的力学特性,本研究进行了蓖麻籽单轴压榨试验,运用粉末压制成型理论中的Doraivelu 屈服准则,建立了蓖麻籽压榨过程中的塑性模型,对蓖麻籽压榨设备的研制具有一定的理论意义.
1 密闭容器单轴压榨试验
1.1 试验材料与方法
试验材料采用湖南省林业科学院培育的“湘蓖一号”蓖麻籽,选取颗粒直径在6~8 mm 颗粒成熟的蓖麻籽进行压榨试验,装料高度为83 mm.
本试验使用仪器为单轴压榨试验装置、Fluke705回路校准器及电子万能试验机.平膜型压力变送器测量侧向压力,压力变送器的输出端接到回路校准器,用回路校准器记录电流值,经换算得到压榨室内的侧向压力,试验装置如图1 所示.在常温下,将50 g“湘蓖壹号”蓖麻籽放入单轴压榨试验装置的压榨腔内,插入活塞,然后将单轴压榨试验装置放置于电子万能试验机上,采用6 mm/min 的加载速度,设定电子万能试验机最大加载压力为64 000 N,每隔10 s记录回路校准器上的电流值,并通过电子万能试验机上的计算机读取轴向加载应力-应变曲线.

图1 单轴压榨试验装置Fig.1 The uniaxial pressing apparatus
1.2 密闭容器单轴压榨试验结果与分析
单轴压榨试验曲线如图2 所示,轴向应力σz和轴向应变εz的定义式分别如下:

式中,F 表示轴向加载压力(N);A 表示单轴压榨腔截面积(1 194 mm2);H0表示物料初始高度(83 mm);H 表示在F 作用下对应的高度(mm).
侧向压力系数公式为:

式中,σr表示回路校准器读取换算得到的侧向压力(MPa);
由公式(1)、(2)可以计算得到轴向应力σz和轴向应变εz(图2),压力变送器和回路校准器可以测得侧向压力σr,试验结果如表1 所示.
在试验过程中发现,轴向应力-应变曲线在初始阶段(压力为900 N 左右)出现了突变,这种现象主要是由蓖麻籽外壳大量破裂引起的.由于蓖麻籽壳与蓖麻籽仁硬度相差较大,在蓖麻籽颗粒被压实和出现大量破碎之前,蓖麻籽散粒体主要表现出蓖麻籽壳的弹性变形,散粒体刚度较大;当压榨力超过了蓖麻籽壳的破碎极限后,蓖麻籽散粒体主要体现为蓖麻籽仁的塑性变形.
从图2 可知,在压榨出油后段,随着载荷的增加,较小的变形量需要施加较大的压力.单轴压榨应力随应变有幂次增长趋势,这是因为在出油后段,出油孔隙被不断压缩而减小,出油越困难,蓖麻籽散粒体表现出压榨强化规律.

图2 轴向应力-应变曲线Fig.2 The curve of axial stress-strain

表1 蓖麻籽单轴压榨试验结果Tab.1 The uniaxial pressing results of castor seeds
2 密闭容器单轴压榨本构模型
2.1 塑性可压缩散粒体屈服条件
由于粉末压制理论惯用方法是将粉末作为可压缩的连续体[8],因此将Doraivelu 屈服准则应用到蓖麻籽散粒体屈服准则需要考虑以下几个问题:①蓖麻籽散粒体体积是可压缩的;②蓖麻籽散粒体流动应力与相对密度有关系,相对密度越大,变形所需的应力就越大[9];③建立蓖麻籽散粒体屈服准则应考虑静水压力的影响.
Doraivelu 屈服准则变形式[3]:

假设蓖麻籽散粒体塑性势能面和屈服面相同,则可将蓖麻籽散粒体屈服函数作为它的塑性势能函数,即流动法则和屈服条件相关联,则有:
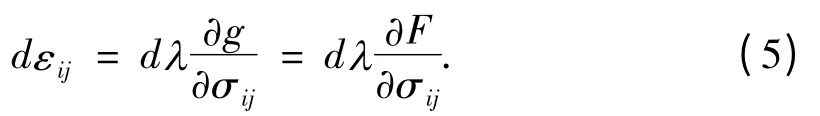
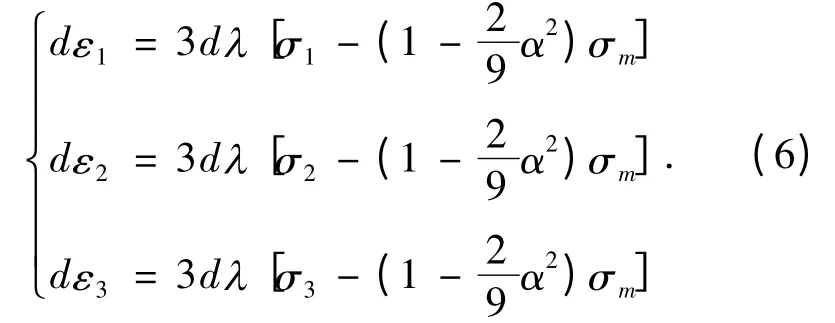


联立公式(6)、(7)可得:
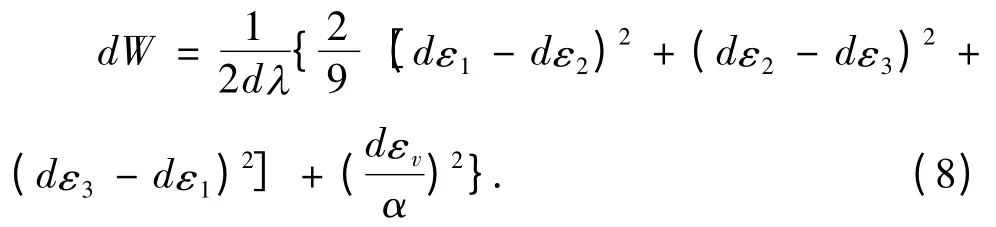
又有dW=dεeqσeq,则分别定义等效应变增量公式dεeq和等效应力公式σeq:

2.2 蓖麻籽散粒体塑性模型
由于蓖麻籽散粒体在密闭容器中受到了周向和径向限制,在加载过程中,蓖麻籽散粒体只能沿轴向被压缩,不能产生侧向变形,则压榨过程中蓖麻籽散粒体的应力-应变状态有:
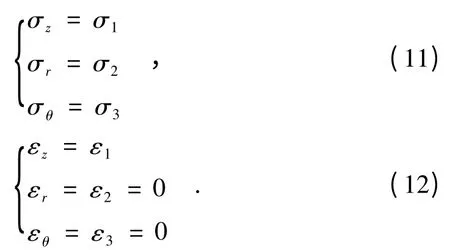
因此前面所示三维塑性模型参数可用轴对称压榨塑性模型参数表示,将式(9)代入(4)、(7)、(8)得:
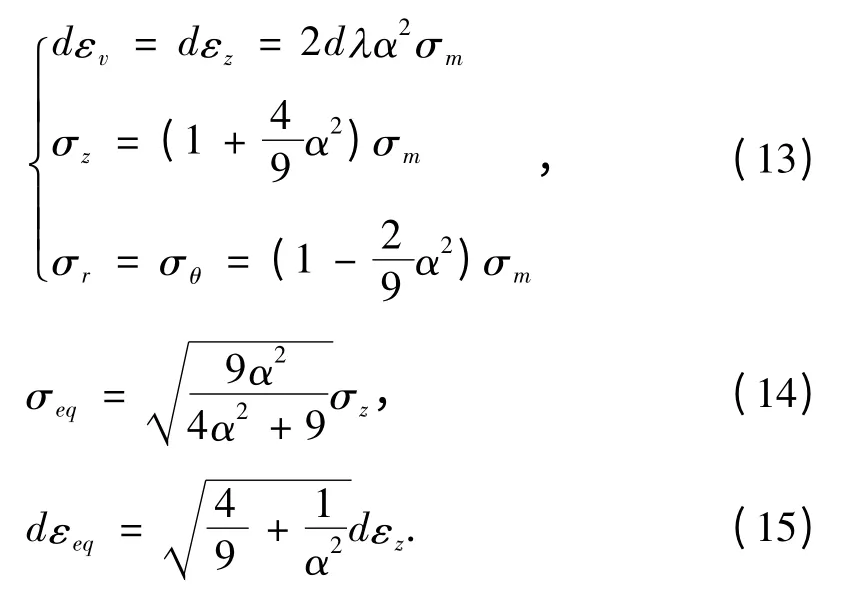
由公式(3)和公式(13)得:

由密闭容器单轴压榨试验,可以直接测量得到σz,σr及dεz,再通过上述方程就可以确定ξ;根据试验结果及式(14)、(15)、(16)可以计算得到蓖麻籽等效应力σeq和等效应变增量dεeq.
在螺旋压榨蓖麻籽的实际生产现场,残存于螺旋榨油机中的蓖麻饼粕经常会出现坚硬的胶质物.通过密闭容器单轴压榨试验结果分析发现,蓖麻籽散粒体载荷位移曲线符合幂次强化规律,因此可设密闭容器单轴压榨本构方程为:
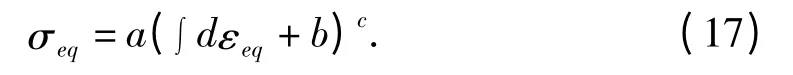
由试验可得侧向压力系数、等效应力及等效应变增量,再由最小二乘法拟合可以得到σeq与∫dεeq的关系式.
经试验数据回归可得a=2.91,b=0.44,c=13.41,塑性模型得到的等效应力-应变曲线和实际测量得到的应力-应变曲线如图3 所示.与图2 比较可知,在相同应力条件下,蓖麻籽散粒体的等效应变要大于单轴加载时的轴向应变.

图3 等效应力-应变曲线Fig.3 The curve of equivalent stress-strain
3 模型验证
3.1 塑性模型的增量公式
由式(14)可得:

由式(17)得:

由于是等速加载,所以dεz可知,由式(15)、(17)、(19)可计算出dεeq,进而可计算得到累加等效应变εeq.整个加载过程持续600 s,取后400 s 的试验数据进行分析,得到应变的计算结果与试验结果如表2 所示.对比发现,由增量公式和全量公式计算得到的等效应变值比较接近.且蓖麻籽散粒体压榨等效应力-应变关系符合幂次强化规律.在相同大小加载力条件下,等效应力-应变模型计算得到的等效应变与单轴加载时实际应变最大相对误差为8.3%,平均相对误差为5.41%,造成这种偏差的原因是在出油后段,油液不断渗出,蓖麻籽散粒体逐渐趋近于致密体.

表2 模型验证结果Tab.2 The results of model validation
3.2 塑性模型的全量公式
由(19)式得∫dεeq=εeq,代入(14)式,则有:

式中,a,b,c 等参数由增量公式已确定,如果给定轴向应力σz和侧向应力σr就可以求得应力强度σeq与系数α 及t 值,由式(20)可以计算出理论等效应变值εeq.全量公式计算结果如表2,对比可知,全量公式和增量公式二者具有一致性.
4 结论
蓖麻籽散粒体在塑性阶段,随着总载荷的增加,出油间隙被不断压榨减小,较小的变形需要施加较大的载荷,表现出幂次强化规律.
基于Doraivelu 屈服准则建立的蓖麻籽散粒体等效应力-应变模型能较好地反映其塑性阶段的力学特性.
由蓖麻籽散粒体塑性模型计算值可知,在塑性阶段,相同大小加载力条件下,等效应变与单向加载时轴向应变最大相对误差为8.3%,平均相对误差为5.41%,本文建立的蓖麻籽冷榨塑性模型能较精确地反映其应力-应变关系.
[1]李诗龙,刘协舫.螺旋榨油机喂料段的理论与实践[J].中国油脂,2004,29(7):15-19.
[2]KHAN L M,HANNA M A.Expression of oil from oil seeds:A review[J].J Agr Eng Res,1983,28(6):495-503.
[3]郑晓,林国祥,王少梅.菜籽与菜籽仁散粒体的压榨塑性模型[J].浙江大学学报:农业与生命科学版,2005,31(6):802-806.
[4]郑晓,林国祥,游燕等.棉籽和蓖麻籽的冷榨试验与数值模拟[J].农业工程学报,2007,23(9):260-264.
[5]张亚新,郑晓,林国祥.葵花籽压榨过程中的塑性模型[J].农业机械学报,2009,40(7):138-142.
[6]赵东,黄文彬,郭康权.玉米秆粉粒体压制成型模型的研究[J].西北农业大学学报,1998,26(5):44-47.
[7]BARGALE P C,FORD R J,SOSULSKI F W,et al.Mechanical Oil Expression from Extruded Soybean Samples[J].J Am Oil Chem Soc,1999,76(2):223-229.
[8]DORAIVELU S M,GEGEL H L,GUNASEKERA J S,et al.A new yield function for compressible materials[J].Int J Mech Sci,1984,26(9/10):527-535.
[9]汪俊,李从心,阮雪榆.基于实验参数修正的粉末金属压制过程数学模型[J].上海交通大学学报,2000,34(3):322-325.
[10]尚福林,王子昆.塑性力学基础[M].西安:西安交通大学出版社,2011:77-78.

