一种用于制作CBERS－02C卫星融合影像的配准方法

陈 奇 ，王 博 ，孙明伟 ，王树根 ，张永军，李 畅

（1.武汉大学 遥感信息工程学院，武汉 430079；2.华中师范大学 城市与环境科学学院，武汉 430079）

2011年12月22 日，资源一号02C（CBERS－02C）卫星在太原卫星发射中心成功发射升空.作为我国首颗国土资源卫星，CBERS－02C 卫星上载有10m 分辨率的多光谱相机（含红外波段、红波段以及绿波段），5 m 分辨率的全色相机，以及2.36m 分辨率的全色高分辨率（HR）相机.与单一的全色影像或低分辨率的多光谱影像相比，两者融合得到的高分辨率彩色影像信息量更丰富，在国土资源调查与监测、防灾减灾、农林水利、生态环境、国家重大工程等领域更具应用价值.

制作CBERS－02C融合影像的关键技术，在于如何实现整景范围内多光谱影像和全色影像的高精度配准.近年来，针对遥感影像配准，国内外许多学者提出了多种方法.其中，张登荣等基于灰度相关的方法，结合影像金字塔进行分层影像匹配［1］，能够自动得到大量均匀分布的同名点，但当初值不准或误匹配较多时，这种处理方式的可行性还有待研究.另有一些学者基于SIFT 特征［2］能够对旋转、尺度保持不变的特性，将其应用至遥感影像配准领域，取得了较好的结果［3－5］，然而基于SIFT 特征匹配得到的同名点往往分布不均，尽管通过分块匹配能够予以改善，但是未匹配到点的局部区域的配准精度仍然偏低.针对灰度匹配和SIFT 特征匹配的优势与不足，有人提出了分阶段进行影像粗配准和精配准的思路.张继贤等提出了先通过多项式模型对影像进行整体粗纠正再利用灰度匹配实施精匹配的方法［6］，并成功实现了基于小面元纠正技术的多源遥感影像自动配准.Yu和翟涌光分别提出将SIFT算法与灰度匹配结合使用的策略［7－8］，以实现由粗到精的影像自动配准，但前者采用小波金字塔实现逐层影像的精匹配，流程较为复杂，后者则直接使用SIFT算法对影像进行粗匹配，没有提及该算法内存消耗多、运算速度慢［4］，并不适合直接用于大像幅遥感影像配准的问题.

此外，CBERS－02C卫星所提供的用于融合的数据源也具有一定特点.目前据初步验证，在通过高精度检校场数据对卫星相机进行检校之后，CBERS－02C 卫星的直接定位精度已经能达到50～100m 左右.但在实际处理中，因为受到卫星抖动、行时不准确等诸多因素的影响，该精度水平往往很难一直保持，目前卫星的直接定位精度尚不稳定.另一方面，由于具备中国国内地区高精度的底图数据，CBERS－02C地面数据处理系统采用相关技术可以获得精化后的卫星定向数据，因此对于国内地区而言，其定位精度始终维持在较高水平（20～40m）；对于境外数据而言，定位精度不稳将可能导致纠正后的多光谱影像与全色影像的坐标存在较大差异.本文采用的试验数据即体现了这种特性.

鉴于此，为了对CBERS－02C 卫星在线提供的全球范围数据进行融合影像的自动化制作，本文设计了一种适用于CBERS－02C 卫星数据的影像配准方法.首先对影像进行几何精纠正并生成缩略图，并采用SIFT 算法对纠正影像的缩略图进行粗匹配，克服卫星定位精度不稳定的困难；然后对已经采样为相同分辨率的纠正影像，进行基于灰度相关的影像精匹配，得到大量均匀分布的同名点；剔除匹配点粗差后，最终通过基于不规则三角网的面元纠正方法实现影像的精确配准.

1 影像几何精纠正

基于共线方程的严密几何成像模型［9］，以业内公开的SRTM－DEM［10］作为高程数据源，采用相同的地面采样分辨率分别对全色及多光谱影像进行几何精纠正.这样做能够在很大程度上解决影像间的旋转角度与尺度差异，降低配准的难度.在纠正的同时通过间隔采样方法生成纠正影像的缩略图，便于随后在缩略图上进行SIFT 粗匹配.

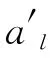
从表1可看出，各组数据内部中同名点的坐标差值并非趋于一致，而是存在一定的差异，这是由于全色相机与多光谱相机的镜头分别存在不同程度的畸变所致.国内影像数据由于定位精度较高，对应同名点之间的坐标差值基本控制在20个像素以内；境外影像数据由于定向精度偏低，其同名点间的坐标差值最高可达到几百个像素.在这种情况下，如果直接利用坐标预测的方法进行灰度匹配，则需要设置非常大的搜索窗口才有可能找到同名点.这将极大地延长匹配用时，也将降低匹配结果的可靠性.可见对于CBERS－02C 影像配准而言，采取由粗到精的匹配策略是十分必要的.

图1 纠正影像上同名像点的坐标差值Fig.1 The coordinate differences of orresponding points on the rectified images

表1 纠正影像同名像点间的坐标差值Tab.1 The coordinate difference between the corresponding points on the rectified images

2 由粗到精的影像匹配策略

在进行基于灰度相关的影像匹配之前，首先采用SIFT 算法［2］对影像缩略图进行粗匹配.SIFT特征匹配算法无需进行区域搜索，其匹配结果在剔除粗差后具有很高的可靠性.虽然这种方法计算量大、相较灰度匹配更加耗时，并不适合直接用于像幅较大的卫星遥感影像之间的匹配，但这种劣势反映到影像缩略图上则基本可以忽略不计.

图2 影像缩略图粗匹配结果Fig.2 Results of the coarse matching between the image thumbnails

以北京地区的数据为例，图2所示为缩略图的SIFT 粗匹配结果.考虑到影像对比度过低可能导致SIFT 算法提取到的特征过少，本文对缩略图均作了对比度增强处理.对表1中相关数据的缩略图逐对进行SIFT 匹配，并利用匹配点求得仿射变换参数，表2所示为经过仿射变换之后检查点的残差情况.

图3所示为粗匹配前后同名检查点间坐标差值的比较.从中可看出，对于CBERS－02C 卫星的几何精纠正影像而言，利用缩略图上同名点进行仿射变换拟合既不会对精度较高的数据产生负面影响，也可实现对精度较差数据的大致拟合，进而保证了下一步进行影像的精匹配时，在预测位置以较小的搜索窗口就能搜索到同名点.

表2 经仿射变换之后同名像点间的坐标残差Tab.2 The residual error between the corresponding points on images after affine transformation

图3 粗匹配前后同名像点的坐标差值比较Fig.3 The coordinate difference between corresponding points on images before and after coarse matching

在进行精匹配之前，需要对影像做以下两个方面处理：首先，将多光谱影像灰度化，并采用Wallis滤波器［11］对全色影像与灰度化的多光谱影像进行增强，这样不仅可以消除影像灰度尺度的不一致，同时可提高影像的信噪比，从而保证影像特征在灰度空间的高相关性.其次，采用改进的Harris算子［12］提取子像素级特征点，通过设置合理的间距将影像划分为格网，可以提取得到均匀分布的特征点.

在对格网中的特征点逐个实施精匹配的过程中，利用粗匹配结果解算得到的变换参数可预测其同名点的概略位置，然后进行基于灰度的相关系数法［13］匹配可得到像素级精度的匹配结果，最后以该结果为初值进行最小二乘匹配［14］，匹配精度将达到子像素级.

3 粗差剔除与影像配准

无论是基于SIFT 特征的粗匹配，还是基于灰度相关的精匹配，其匹配结果都必须进行粗差剔除以保证其可靠性.

由于CBERS－02C 卫星的全色相机与多光谱相机的镜头畸变特点与变形程度都各不相同，再加上几何精纠正影像的生成已经历了复杂的处理流程，因此很难使用严格的数学模型来精确描述影像之间的坐标对应关系，作为影像匹配粗差剔除的依据.但是，若将判定粗差的区域缩小至影像局部小范围内，往往可以将成像畸变的影响最小化，又由于影像已经过纠正处理，故利用简单的数学模型（如旋转平移模型、仿射变换模型等）即可对小范围内同名点的坐标关系进行逼近，进而对匹配粗差进行有效剔除.

如图4所示，将待判定的匹配点与其附近的其他匹配点构建三角网之后可以看到：（a）中的a1与a2为左右影像中的正确匹配点，尽管影像间存在畸变，但通过局部模型变换可以将该畸变消除，故该点将不会被视为粗差；对于（b）中的错误匹配点b1和b2，通过计算可知其局部模型误差要明显大于周边的匹配点，从而可以探测出该粗差.

综上所述，本文剔除粗差的具体算法可分为以下几步：

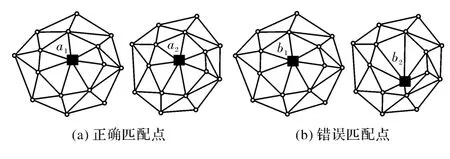
图4 影像匹配粗差剔除示意图Fig.4 Blunder elimination of matching points

1）依据任一影像的像方坐标，采用分割归并法［15］构建匹配点集的三角网结构；

2）对三角网内的点逐一进行判定，每判定一个点，首先利用三角网的结构关系搜索出与其距离小于一定阈值的若干个点，再利用该点集及其匹配点的像方坐标，建立局部旋转平移变换模型，并进行最小二乘模型解算；

3）若待判定点的模型误差大于一定阈值，则在匹配点集中将其作为粗差剔除，否则转至步骤2）对下一点进行判定；

4）遍历完三角网内所有的点之后，重复步骤1）到步骤3），直至所有点位均能满足局部模型关系，算法结束.

由于CBERS－02C 纠正影像的精度受到诸多因素的影响，所以不论是用仿射变换、几何多项式或是更为复杂的约束模型都无法精确的描述整幅影像之间的几何畸变，其配准精度也不足以用于制作高质量的融合影像.因此，本文基于剔除粗差后的匹配点集构建的不规则三角网，将全色影像分割成为一个个三角形，根据匹配点可以找到对应多光谱影像上的同名三角形，然后利用仿射变换模型拟合同名三角形之间的局部影像畸变，由三对同名顶点坐标求得变换系数后，再以单个三角形为单位进行面元纠正，从而实现影像的精确配准.

4 试验与分析

为了验证自动制作CBERS－02C 融合影像的可行性，笔者对前文所述的3组CBERS－02C 影像进行了配准试验，包括北京城区数据、河北承德的山区数据以及东京沿海地区数据各1组.其中全色影像像幅大小为12 000×12 000pixel，多光谱影像为6 000×6 000pixel，HR 影像约为24 000×24 000pixel.

在进行配准处理之前，首先对各组影像完成几何精纠正处理.对于每1组影像，均保证多光谱与全色影像的采样分辨率保持一致（2.5m 或5m），此外为了能够得到更好的粗匹配结果，在保留影像原始宽高比的前提下将各类型纠正影像缩略图的大小均控制在1 400×1 400pixel左右.

表3对3组试验数据的精匹配结果进行了统计，其中“正确点”表示剔除粗差后剩余的匹配点，“正确率”是指正确点数相较匹配点数的百分比.试验中匹配窗口大小为13×13，搜索窗口大小为51×51，相关系数阈值为0.85.设置较大的匹配窗口和较小的搜索窗口使得精匹配中的同名点具有较高的精度和可靠性.从表3可看出算法具有较高的匹配成功率，且对于各种地形的数据均有较好的适应性.东京地区由于匹配影像的原始分辨率相差较大（2.36m 和10 m）、信息量过于不对称，从而导致匹配点相对较稀疏，且产生了较多的误匹配，但在粗差剔除之后，总体上仍然得到了大量均匀分布的正确匹配点.

表3 影像精匹配结果Tab.3 Results of precise image matching

图5所示为北京地区试验数据的精匹配结果，以红色标记的点为被剔除掉的粗差点.可以看到，匹配得到的同名点分布均匀，且具有一定的密度.对这些同名点构建不规则三角网，然后利用扫描线算法，进行逐个三角形的面元纠正，最终可完成影像配准.

为了验证算法的效率，笔者在一台具有双核CPU，主频为2.50GHz，内存为2.00GB，操作系统为Microsoft Windows XP的计算机上对算法的耗时进行了统计，并通过计算同名检查点的坐标中误差来检验配准精度.表4所示为试验的精度和耗时情况.从中可看出，本文的配准精度已经达到子像素级，配准算法的时间效率也较高，完全能够满足准实时处理的要求.

表4 影像配准的精度和效率Tab.4 Accuracy and efficiency of image registration

完成配准之后，图6所示为对各组影像利用IHS变换法［16］进行融合后得到的3景影像（亮度已经过调整）.可以看出，无论是飞机的机翼、山脊线还是建筑物的棱角等影像细节都表现出良好的融合效果.融合影像既能清晰地表达地物的细节特征，同时又具备较为丰富的光谱信息，应用价值较高.

图6 CBERS－02C全色与多光谱影像融合结果Fig.6 Results of the images fused from the panchromatic and multispectral imagery of CBERS－02C

5 结论

针对CBERS－02C 卫星无法在全球范围内均保持较高定位精度，从而导致全色与多光谱影像有可能存在较大精度差异的运行特点，本文提出了一种影像自动配准方法，能够成功用于制作CBERS－02C高分辨率彩色融合影像.试验表明，本文提出的方法实用有效，能够对多种类型的数据实现影像精配准，其配准精度达到子像素级.目前，该方法已成功应用于中国资源卫星应用中心地面数据处理系统，在并行计算环境下已经实现CBERS－02C 卫星地面数据的自动化准实时处理.对于其他类型的光学卫星遥感影像数据而言，本文的处理方法同样具有参考价值.

［1］张登荣，俞 乐，蔡志刚.点特征和小波金字塔技术的遥感图像快速匹配技术［J］.浙江大学学报：理学版，2007，34（4）：465－468.

［2］Lowe D G.Distinctive image features from scale invariant Keypoints［J］.International Journal of Computer Vision，2004，60（2）：91－110.

［3］李晓明，郑 链，胡占义.基于SIFT 特征的遥感影像自动配准［J］.遥感学报，2006，10（6）：829－835.

［4］朱志文，沈占峰，骆剑承.改进SIFT 点特征的并行遥感影像配准［J］.遥感学报，2011，15（5）：1032－1039.

［5］WANG Li，NIU Zheng，WU Chaoyang，et al.A robust multisource image automatic registration system based on SIFT descriptor［J］.International Journal of Remote Sensing，2012，33（12）：3850－3869.

［6］张继贤，李国胜，曾 钰.多源遥感影像高精度自动配准的方法研究［J］.遥感学报，2005，9（1）：73－77.

［7］Yu L，Zhang D R，Holden E J.A fast and fully automatic registration approach based on point features for multi－source remote sensing images ［J］.Computers ＆ Geosciences，2008，34（7）：838－848.

［8］翟涌光，王耀强.基于点特征的多源遥感影像高精度配准方法［J］.遥感技术与应用，2010，25（3）：403－409.

［9］张永生，巩丹超，刘 军.高分辨率遥感卫星应用［M］.北京：科学出版社，2004.

［10］Foni A，Seal D.Shuttle radar topography mission：an innovative approach to shuttle orbital control［J］.Acta Astronaut，2004，54：565－570.

［11］张 力，张祖勋，张剑清.Walllis滤波在影像匹配中的应用［J］.武汉测绘科技大学学报，1999，24（1）：24－27，35.

［12］谢东海，詹总谦，江万寿.改进Harris算子用于点特征的精确定位［J］.测绘信息与工程，2003，28（2）：22－23.

［13］张剑清，潘 励，王树根.摄影测量学［M］.武汉：武汉大学出版社，2003.

［14］Rosenhol D.Multi－point matching using the least squares technique for evaluation of three－dimensional models［J］.Photogrammetric Engineering and Remote Sensing，1987，53（6）：621－626.

［15］邵春丽，胡 鹏，黄承义，等.DELAUNAY 三角网的算法详述及其应用发展前景［J］.测绘科学，2004，29（6）：68－71.

［16］Schetselaar E M.Fusion by the IHS transform：Should we use cylindrical or spherical coordinates？［J］.International Journal of Remote Sensing，1998，19（4）：759－765.