用标贯击数评价黏性土物理参数

张 坤，王 迅

(中水东北勘测设计研究有限责任公司，吉林 长春 134001)

0 引言

黏性土的液性指数是评价估算黏性土的物理、力学性质的重要指标。在野外勘察中，受岩心摆放时间、气温、地质人员工作经验的影响，判定的塑性状态与室内试验值经有常较大出入，因此建立岩土物理参数与标贯试验(SPT)击数N 的经验关系式，不失为一种比较科学、直观的方法。

本文分析了哈尔滨市松北灌排体系及水生态环境建设工程2009年—2011年具有代表性的标贯试验与土工试验资料，对其进行一元线性回归分析，建立线性回归方程。设以变量X 代替标准贯入试验实测锤击数N，以变量Y 代替黏性土状态指标IL。

1 数据选取

哈尔滨市松北灌排体系及水生态环境建设工程位于松花江左岸、哈尔滨市松北区，共完成勘探钻孔4 000余个，总进尺3 万余米，土样试验组数5 500 余组。本区第四系地层广布，厚度30～80 m，由于淤泥质黏土标贯击数极低，无评价意义，本文针对湖积环境灰色黏土及灰色粉质黏土进行统计，共收集367 组黏性土原状样土工试验成果，对应标贯组数304 组。根据土工试验成果中塑性状态和标贯击数分别进行统计，计算其平均值φm、标准差σf、变异系数δ［1－3］。

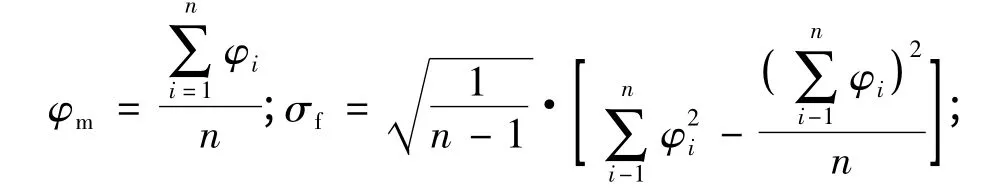
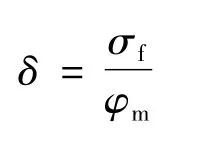
试验指标中的重大失误或非代表性的数据用Grubbs 准则判别，并采用三倍标准差法剔除异常数据，然后进行统计分析。统计数据见表1、表2。

2 一元线性回归分析

一元线性回归数学模型Y=f(X，u)，设回归系数为a、b。利用最小二乘法:

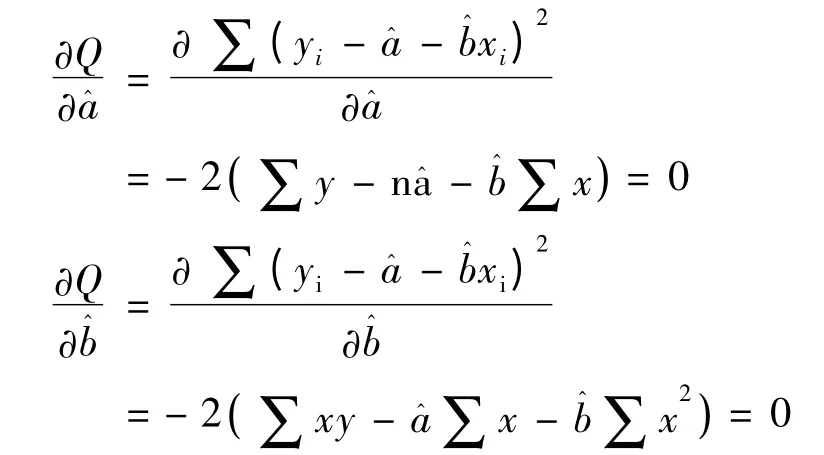
由此求出回归系数:

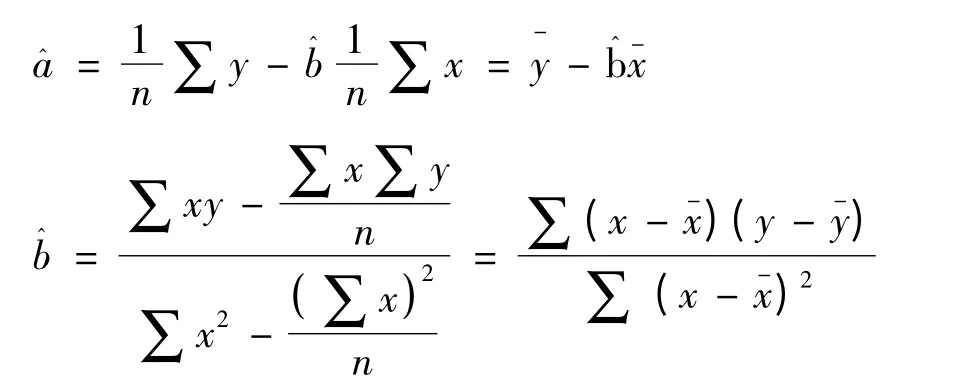
将表1 中标贯击数N 定义为X 轴，液性指数IL定义为Y 轴，分别做出黏土与粉质黏土的标贯击数—液性指数散点图，见图1～2。

如图容易得出变量X、Y 之间存在线性相关关系，建立Y 倚X 线性关系。得出回归方程(见表3):

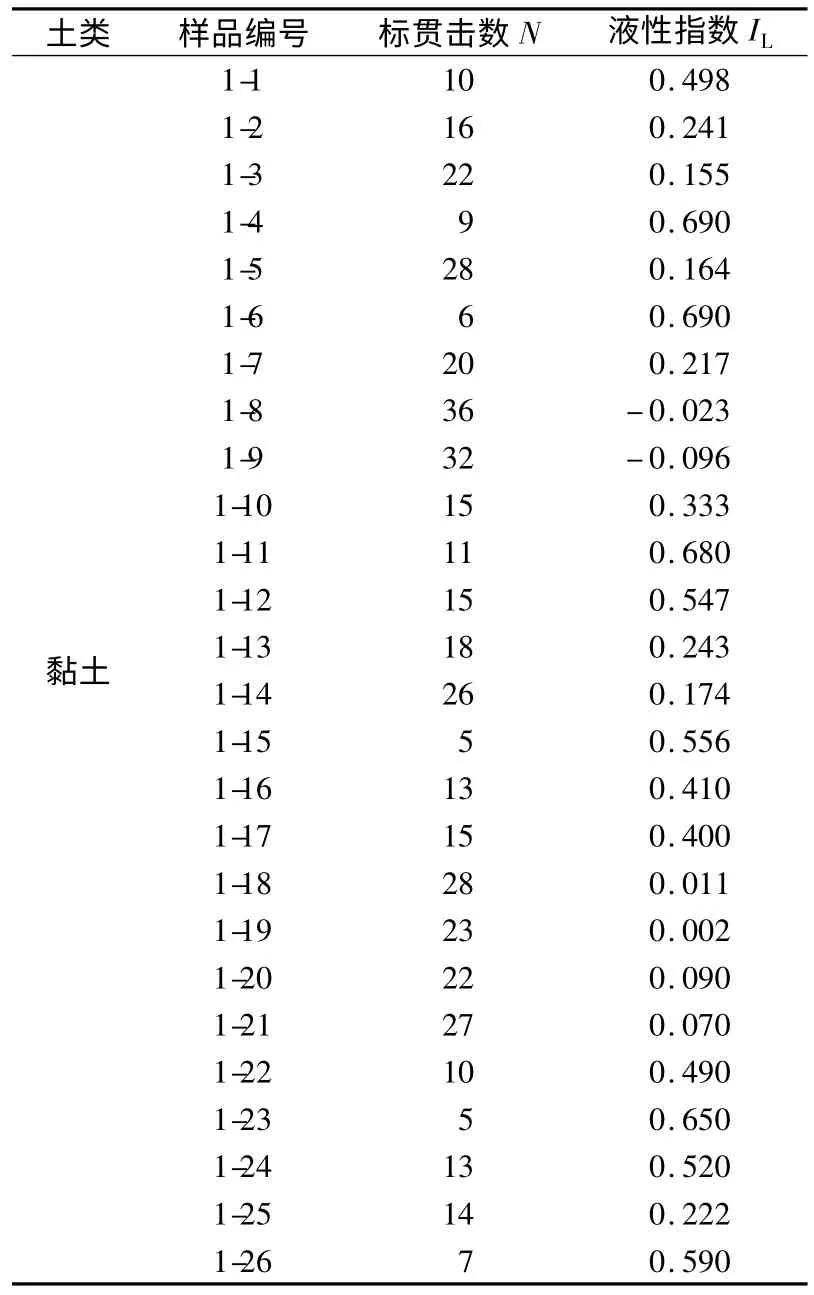
表1 黏土标贯击数与液性指数统计表Table 1 Statistical table of SPT blow count of clay and liquidity index

表2 粉质黏土标贯击数与液性指数统计表Table 2 Statistical table of SPT blow count of silt clay and liquidity index

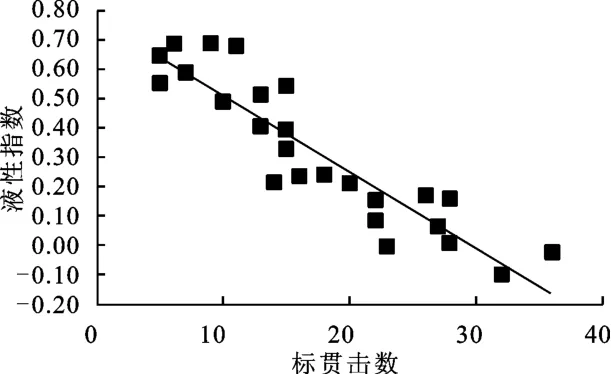
图1 液体指数—标贯击数(粘土)Fig.1 Liquidity index-SPT blow count

表3 回归方程表Table 3 Regression equation

图2 液性指数—标贯击数(粉质粘土)Fig.2 Liquidity index-SPT blow count(silt day)

相关系数位于0.90 左右，可见标贯击数与液性指数存在较高的线性关系，液性指数随标贯击数的增加而减小。并且黏土与粉质黏土的N-IL 线性方程相差不大，可合并黏性土经验公式:IL=－0.026N +0.790。

表4 标贯经验公式表Table 4 Table of empirical formula of standard penetration

3 公式验证与应用

为了验证该公式，把回归预测值与实际物理参数作比较，抽取松北区松花江避暑城内河水系工程及松北灌排体系补充工程中30 组原状土室内试验来验证，液性指数偏差算数平均值为9.87%，较接近，验证了回归方程的适用性。

另根据经验公式得出表4。

该表与地质工程手册(第四版)“实测击数N 和黏性土液性指数IL的关系”存在部分差异，笔者认为，当采用标准贯入试验测试岩土的物理力学参数时，锤击数与岩土参数的关系在不同地区、不同地质条件下存在显著的差异。尤其中国幅员广阔，地形复杂多样，各地区土质条件各异，所以，这些关系式的建立仅对该地区岩土参数的设计应用起到重要作用。

4 结论

利用哈尔滨松北区的大量黏性土试验资料，通过线性回归法得出标贯击数N 与黏性土液性指数IL的相关性。证明了两者存在线性关系。

此计算方法同样适用于标贯击数与压缩模量N-ES、压缩系数N-a 等，经过统计，N-ES、N-a 同样存在线性关系，此文不再详细说明。

本经验公式仅供参考于哈尔滨松北地区或同类地质条件的非流塑黏性土。随着更多数据的收集与统计，可以对该公式继续修正，以求更加精确，为类似工程及建立地区经验公式提供参考。

［1］GB50021—2001，岩土工程勘察规范［S］.

［2］马良荣.标准贯入试验击数与砂土参数间的统计关系［J］.电力勘测设计，2009(3):5－8。

［3］盛骤，谢式千，潘承毅.概率论与数理统计［M］.第三版.北京:高等教育出版社，2001.

［4］工程地质手册编委会.工程地质手册［S］.第四版.北京:中国建筑工业出版社，2007.