无压六圆弧蛋形断面隧洞正常水深的简化计算

滕 凯

(齐齐哈尔市水务局，黑龙江省齐齐哈尔市 161006)

由于蛋形断面与其他断面形式 (马蹄形、门洞形、圆形及矩形等)相比具有受力条件好、过流能力强、适应地质环境能力突出、节省空间及材料显著等优点，因此，随着水利机械化施工技术及工艺的不断提高，该种断面正在越来越广泛地应用于水利水电供排水工程［1，2］。随着工程综合技术的进一步发展，该种断面必将以其突出的优越性在未来的输配水工程中发挥越来越重要的作用。

由于该种断面由六个圆心三个不同半径的六段连续的圆弧曲线构成，几何图形复杂，正常水深计算不但涉及四个区间的分段函数而且需完成超越方程求解，常规的解析法不能直接获解，试算法［3，4］由于公式分段、表达形式为繁复的超越方程，大量的重复计算不但过程繁索，且易出错、精度差、效率低，不便实际应用，利用微机编程求解又不便于实际工作。因此，研究提出一种方便实际工程应用的简化近似计算方法具有重要的意义，而将六圆弧蛋形断面正常水深计算的分段函数统一由一个近似计算公式表示并直接解算，到目前为止尚未见到相关研究成果。

为了解决常规算法及目前现有研究成果所存在的问题，本文依据优化拟合原理，取目标函数为标准剩余差最小，经逐次逼近拟合计算，获得了在工程实用范围内用一个计算通式直接完成求解计算的简化解析式，使求解计算过程更加简捷、直观，便于实际应用。

1 蛋形断面正常水深的基本计算公式

根据明渠均匀流基本方程［5］，六圆弧蛋形过水断面正常水深应按下式计算:

式中 Q——渠道通过流量，m3/s;

A——过水断面面积，m2;

χ——湿周，m;

i——隧洞底坡降;

n——隧洞内壁糙率系数。

1.1 蛋形断面水力要素

六圆弧蛋形过水断面 (见图1)是由三种不同长度的半径分别在六个圆心位置通过弧线构成的闭合曲线，其半径分别为r1、r2和r3。各圆弧段所对应的圆心角分别为 α1、α2、α3和 α4。其数值关系为:

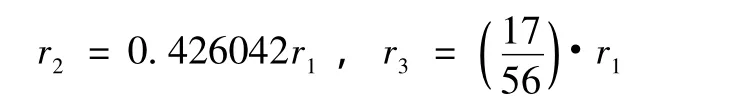
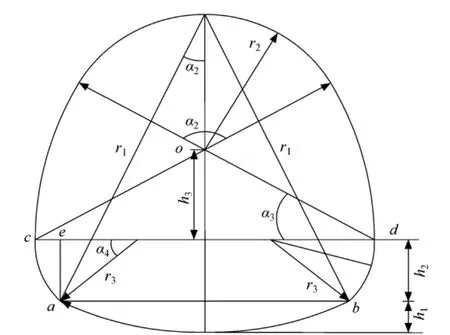
图1 六圆弧蛋形断面

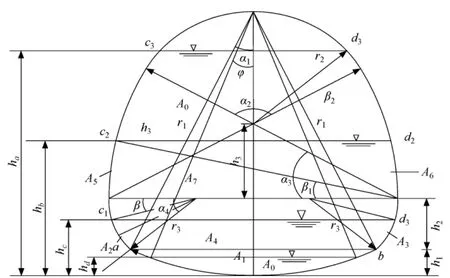
图2 六圆弧蛋形断面计算图

由图1的几何关系可以求得:h1=0.096478r1，h2=0.195651r1，其水力要素为［6］

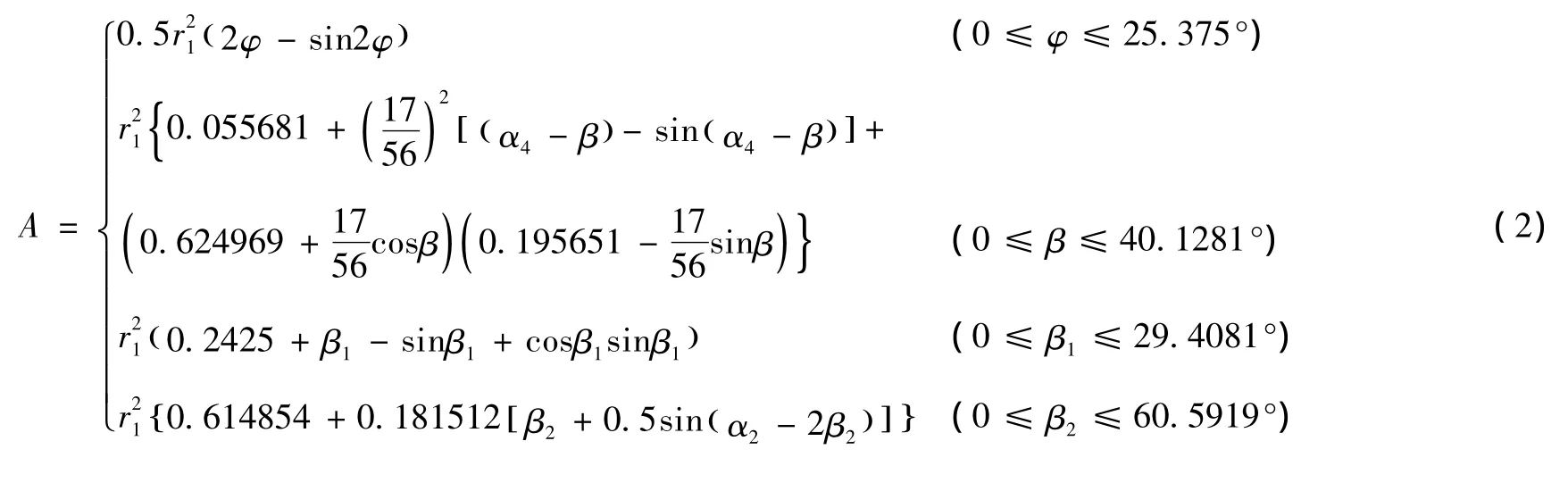
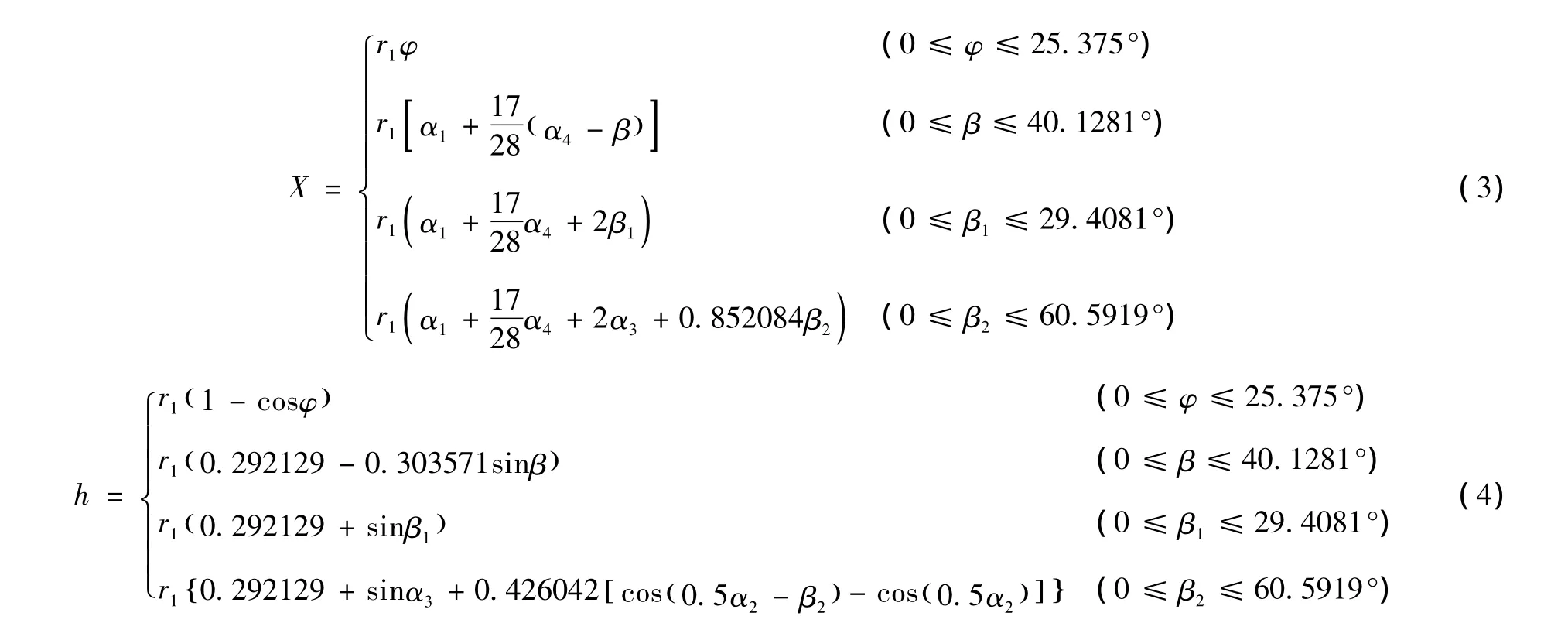
以上式中 h——洞内水深，m;

φ、β、β1、β2——与 α1、α4、α3、α2同圆心的不同区段水深所对应的圆心角 (见图 2)，rad。

1.2 蛋形断面正常水深基本计算公式

将蛋形断面四个区段所对应的水力要素式式(2)～式 (4)分别代人式 (1)，并设

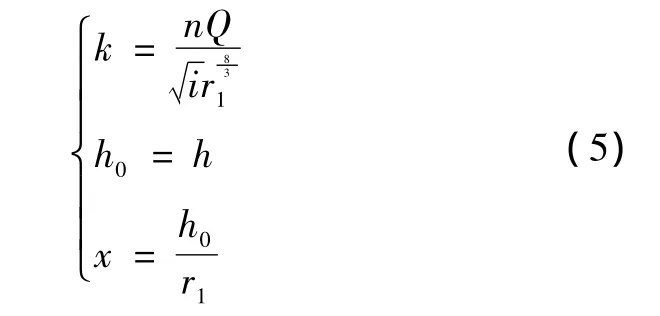
式中 k——已知综合参数;

h0——蛋形断面的正常水深，m;

x——无量纲正常水深，m。

经进一步整理即可获得求解六圆弧蛋形过水断面正常水深的基本公式为

式 (6)为对应自变量x四个区间的四个超越方程，利用式 (6)即可根据已知的k值采用相应区间的计算公式通过非解析法完成无量纲正常水深x的求解，进而由下式求得正常水深，即

由式 (6)可见，x的取值范围为四个连续区间，值域为 ［0，1］，而在实际工程中，x＜0.09情况极为少见;同时，考虑为避免洞内产生不稳定的半有压流现象，《水工隧洞设计规范》［7］规定，洞内水面线以上的富余空间面积不宜小于隧洞断面积的15%，且净空高度不应小于0.4m，由此可以求得x＜0.775，因此，本文将x的取值范围确定为 ［0.09，0.8］，相应参数k的取值范围为 ［0.012，0.360］。

2 蛋形断面正常水深的近似公式及精度分析

2.1 近似公式的建立

由式 (6)可见，该方程为含未知量x的不连续分段超越方程，无法直接获解。为解决这一复杂方程的求解问题，在工程实用参数范围内 (即0.09≤x≤0.8，0.012≤k≤0.360)，假定函数x=f(k)可以替代式 (6)，依据式 (6)即可通过设定不同的x求得k，并展绘x－k关系曲线 (限于篇幅，本文曲线图略)，根据曲线图形关系，经多组备选函数的数值拟合分析及回归计算，以标准剩余差最小为最终希望目标函数［8-15］，即

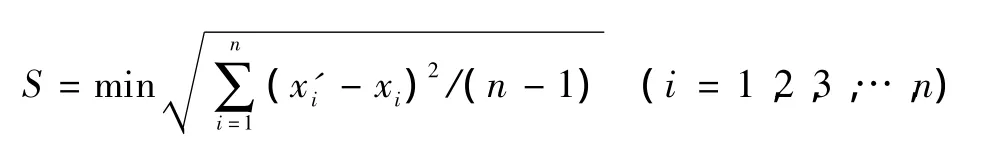
n——拟合计算的数组数。经逐次逼近拟合［16，17］即可获得如下替代函数，即

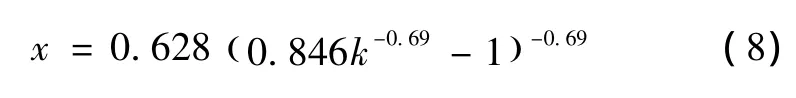
利用式 (8)即可根据已知的k值直接求解无量纲正常水深x，进而完成正常水深h0计算。

2.2 近似公式的精度分析

式 (8)与式 (7)拟合精度的高低，将直接关系到利用式 (8)计算正常水深的成果精度。为比较近似公式 (8)与由四个分段函数构成的公式 (7)的拟合精度，在工程实用参数范围内，选取不同的xi，并根据xi所在区间代入式 (7)与其相对应的区段函数即可分别计算出与之相对应的ki，再将ki代入式(8)求得与之相对应的，并由式 (9)完成拟合相对误差计算。计算结果见表1。

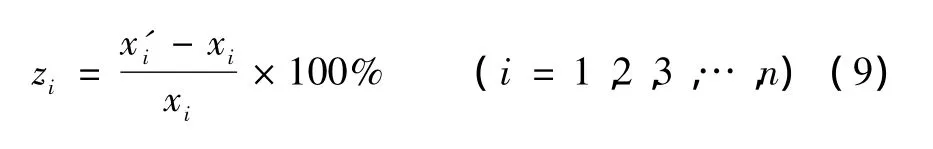
式中 zi——拟合相对误差，%;

i——在拟合计算中所选取的第i个数据。

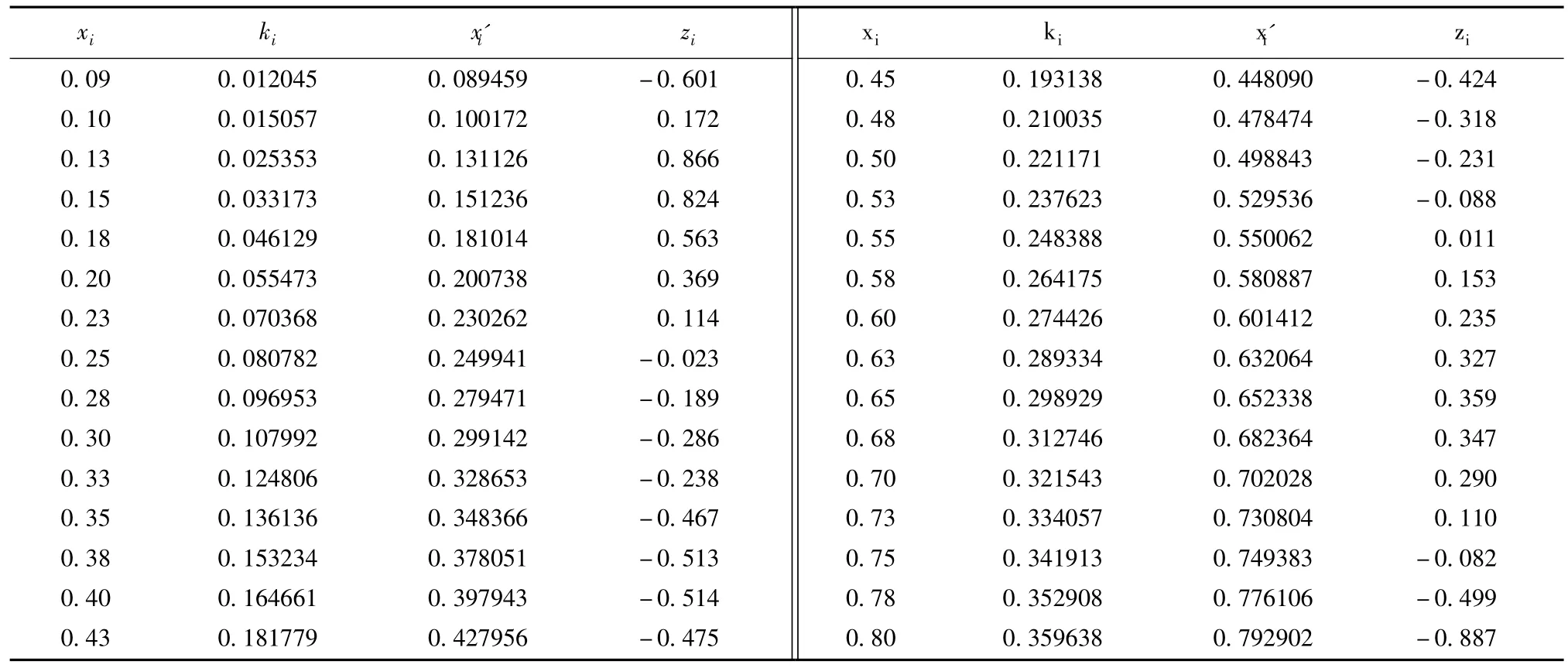
表1 式 (8)拟合精度比较

由表1可见，在工程实用参数范围内，用本文式(8)替代由四个区段函数组成的式 (7)的最大拟合替代相对误差仅为0.887%，且位于常用区域边缘，平均相对误差为－0.019%，且拟合相对误差小于0.5%的点占总计算点数的83.3%。可见，本文式(8)具有较高的拟合替代精度，完全可以满足实际工程的设计精度要求。

3 应用举例

已知某输水隧洞为六圆弧蛋形断面，最大半径r1=1.5m，洞底设计坡降i=1/2500，洞内壁糙率系数n=0.014。试求当设计流量Q=0.1～1.2m3/s时隧洞内相应的正常水深h0值。

当设计流量为Q=0.5m3/s时，根据已知参数即可求得k值为

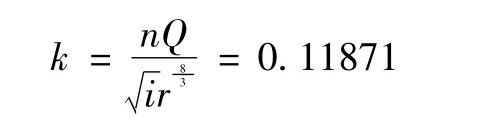
将参数k=0.11871代人式 (8)即可求得无量纲水深为

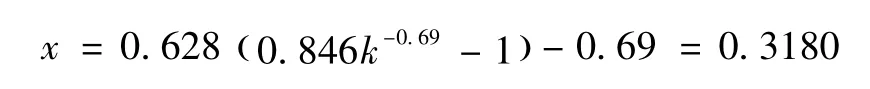
则可求得正常水深h0为

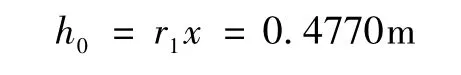
通过微机编程可求得该断面正常水深的精确解为h0=0.4787m，本文简化公式的计算相对误差为－0.355%。

采用同样方法即可完成隧洞在通过其他流量情况下的正常水深计算，并进行精度比较，成果见表2。

表2 正常水深计算成果

由表2可见，在上述参数计算范围内，本文式(8)计算值与理论计算值的最大正、负相对误差分别为0.796%和－0.513%，式 (8)具有较高的计算精度。

4 结语

六圆弧蛋形过水横断面几何图形比较复杂，采用常规计算方法求解正常水深不便实际应用。本文依据优化拟合理论，经逐次逼近计算，获得了可直接完成该断面正常水深求解的近似计算通式，其主要优点如下:

(1)所建立的简化公式在工程实用参数范围内不分段，可使正常水深计算将四个分区函数由一个表达通式完成，避免了分段公式在求解计算中所带来的诸多不便。

(2)公式仅用一个简单的复合幂函数即完成了拟合替代，表达形式简单明了，便于工程技术人员记忆，实现了计算简单、快捷 (仅借助计算器即可)，有效提高了工作效率，具有实际应用推广价值。

(3)该近似计算公式为通过多组函数优化比选所得，具有较好的拟合精度。分析及算例计算结果比较表明:在实用参数范围内，本文公式具有较高的计算精度，其最大计算相对误差不超过0.887%，完全可以满足实际工程的设计精度要求。

［1]傅功年，唐耿红.冉铺湾隧洞衬砌断面型式选择［J］.人民长江，2002(5):14-16.

［2]王子宜.蛋形衬砌在白连灌区武家坳隧洞中的应用［J］.湖南水利水电，2006(6):70-71.

［3]华东水利学院主编.水工设计手册［M］.北京:水利电力出版社，1986.

［4]武汉水利电力学院水力学教研室主编.水力计算手册［M］.北京:水利电力出版社，1983.

［5]清华大学水力学教研室主编.水力学 ［M］.北京:高等教育出版社，1980.

［6]李若冰，张志昌.明渠六圆弧蛋形断面临界水深和收缩断面水深的计算［J］.武汉大学学报 (工学版)，2012(4):463-467.

［7]DL/T 5195—2004水工隧洞设计规范 ［S］.北京:中国电力出版社，2003.

［8]赵延风，刘军，梅淑霞等.普通城门洞形断面正常水深的近似计算方法 ［J］.武汉大学学报:工学版，2009(6):773-775.

［9]张宽地，吕宏兴，赵延风.普通城门洞断面正常水深的近似计算式［J］.长江科学院院报，2010(2):34-36.

［10]刘刚，滕凯.梯形断面均匀流水深的近似计算公式 ［J］.水利与建筑工程学报，2012(1):41-44.

［11]谢成玉，滕凯.三次抛物线形渠道断面收缩水深的简化计算 ［J］.南水北调与水利科技，2012(2):148-150.

［12]谢成玉，滕凯.抛物线形断面渠道均匀流水深的近似计算公式 ［J］.水电能源科学，2012(7):94～95，172.

［13]郑博，滕凯.马蹄形隧洞过水断面临界水深的简化计算法［J］.中国水能及电气化，2012(8):13-17.

［14]滕凯.标准门洞形隧洞正常水深的简易算法 ［J］.中国水能及电气化，2012(9):30-33.

［15]滕凯.消力池深的简化计算法 ［J］.人民长江，2012(15):77-79，91.

［16]王慧文，偏最小二乘回归法及其应用［M］，北京:国防工业出版社，1999.

［17]阎凤文，测量数据处理方法 ［M］，北京:原子能出版社，1988.