中国新一代大地基准—2000国家大地坐标系*
蔺文彬 战兴华 李厚朴
(1.海军驻长春地区航空军事代表室 长春 130033)(2.海军司令部航海保证部 北京 100841)(3.海军工程大学导航工程系 武汉 430033)
1 引言
大地坐标系是地球空间框架的重要基础,是表征地球空间实体位置的3维参考基准,科学地定义和采用国家大地坐标系将会对航空航天、导航定位、地震监测、地球物理勘探等许多领域产生重大影响[1~3]。按其原点相对地球质心的位置,大地坐标系分为参心坐标系和地心坐标系。参心坐标系的原点偏离地心可能达几十到几百米,而地心坐标系的原点理论上与地心重合,实际上与地心难免有些偏离[4~5]。
20世纪80年代以来,空间技术得到了快速发展,利用空间技术所得到的定位成果,都是以地心坐标系为参照系的,传统的参心坐标系已不适应经济社会发展的需要。为了更加科学地描述动态的地球,阐明地球上各种地理和物理现象,为信息化社会发展提供一个基础地理平台,世界上许多发达国家多年前就开始采用地心坐标系,如美国、加拿大、墨西哥、澳大利亚、新西兰、日本、韩国等。地心坐标系统及其框架正在逐渐取代传统的非地心大地坐标系统及其框架[6~7]。
新中国成立以来,我国先后使用过1954年北京坐标系、1980年西安坐标系和新1954年北京坐标系,这些坐标系均为参心坐标系,曾在我国的经济建设和国防建设中发挥过巨大作用,但其成果受当时的技术条件制约,精度偏低,已不能适应科学技术特别是空间技术的发展需要[8~9]。鉴于经济、社会和科学技术发展的需求,我国已从2008年7月1日起正式启用地心三维大地坐标系—2000 国家大地坐标系(CGCS2000)作为新一代的大地基准。
2 2000国家大地坐标系(CGCS2000)的定义及其实现
2.1 2000国家大地坐标系(CGCS2000)的定义
我国采用的三维地心坐标系统CGCS2000的定义和迄今为止比较符合客观实际的ITRS的定义在原则上保持一致,即符合下列条件:
1)它是地心的,地心被定义为包括海洋和大气的整个地球的质量中心;
2)长度单位为引力相对论意义下的局部地球框架中的米;
3)它的定向初始值由1984.0时国际时间局(BIH)的定向给定;
4)定向随时间的演变由整个地球的水平构造运动无净旋转条件保证。
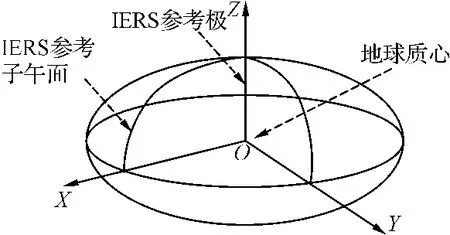
图1 CGCS2000定义的示意图
如图1所示,CGCS2000为右手地固正交坐标系,它的原点和轴向定义如下:
1)原点在地球质量的中心;
2)Z轴指向IERS参考极(IRP)方向;
3)X轴为IERS参考子午面(IRM)与通过原点且同Z轴正交的赤道面的交线;
4)Y轴与Z、X轴构成右手正交坐标系。
CGCS2000的参考椭球为一等位旋转椭球,其椭球面是一等位面。CGCS2000的参考椭球的几何中心与坐标系的原点重合,旋转轴与坐标系的Z轴一致。参考椭球面在几何上是测量计算的基准面,在物理上是地球正常重力场的参考面。CGCS2000参考椭球的四定义常数是:长半轴a=6378137m,扁率f=1/298.257222101,地心引力常数GM=3.986004418×1014m3s-2,地球自转角速度ω=7.292115×10-5rad s-1。
根据以上四个定义常数,文献[10]导出了一系列常用的几何常数和物理常数,如表1和表2所示。

表1 CGCS2000参考椭球导出的几何常数
2.2 2000国家大地坐标系(CGCS2000)的实现
2000国家大地坐标系的实现分为3个层次[9]:
第一层次为CGCS2000 连续运行GPS 网。我国维持CGCS2000主要依靠连续运行GPS观测站,它们是GPS2000的骨架,其坐标精度为毫米级,速度精度为1mm/a。

表2 CGCS2000参考椭球导出的物理常数
第二层次为“2000国家GPS大地控制网”,包括中国全部领土和领海的高精度GPS网点,即全国GPS一、二级网、国家GPS A,B级网、地壳运动监测网和地壳运动观测网络工程网,共约2500多点,它是在国际IGS站以及中国地壳运动观测网络工程网点的控制下经联合平差组成,其三维地心坐标精度约为3cm。
第三层次为全国天文大地控制网(约有50000点)。它是CGCS2000的加密框架。它由全国天文大地网与2000GPS控制网联合平差后的网点坐标体现,三维点位误差约为0.3m,大地高误差不超过0.5m。
3 CGCS2000与WGS84的比较分析
当前已拥有大量GPS数据,并且GPS仍是未来主要的空间数据源之一,鉴于GPS使用WGS84坐标系,为更好地指导实践工作,有必要对CGCS2000与WGS84进行比较分析。
在定义上,CGCS2000与WGS84是一致的,即关于坐标系原点、尺度、定向和定向演变的定义都是相同的。两个坐标系使用的参考椭球也非常接近,具体地说,在4个椭球定义常数中,唯有扁率有微小差异:fCGCS2000=1/298.257222101,fWGS84=1/298.257223563,扁率差异df=1.64348×10-11。椭球扁率差异将导致同一点在两种坐标系内的大地坐标产生差异,也将导致椭球面上的正常重力和正常重力垂直梯度产生差异,文献[10]对此进行了详细的分析。
3.1 两种坐标系下大地坐标的差异
同一点在两种坐标系内的大地经度相同,椭球扁率差异将导致大地纬度、大地高产生变化。同一点在CGCS2000和WGS84下大地纬度的差异dB如图2所示,大地高的差异如图3所示。按5°的纬度间隔,自赤道至北极的范围内,dB和dH的具体数值列于表3所示。
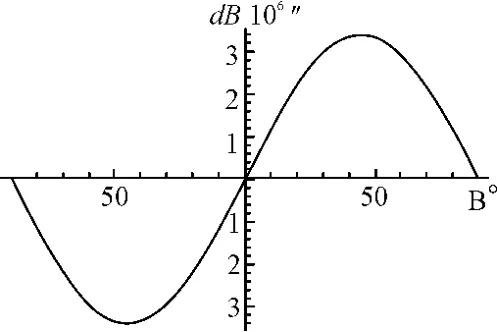
图2 同一点在CGCS2000和WGS84下大地纬度的差异
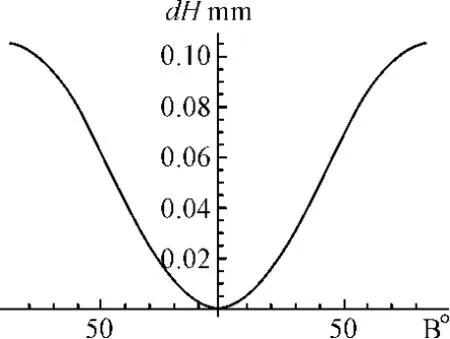
图3 同一点在CGCS2000和WGS84下大地高的差异
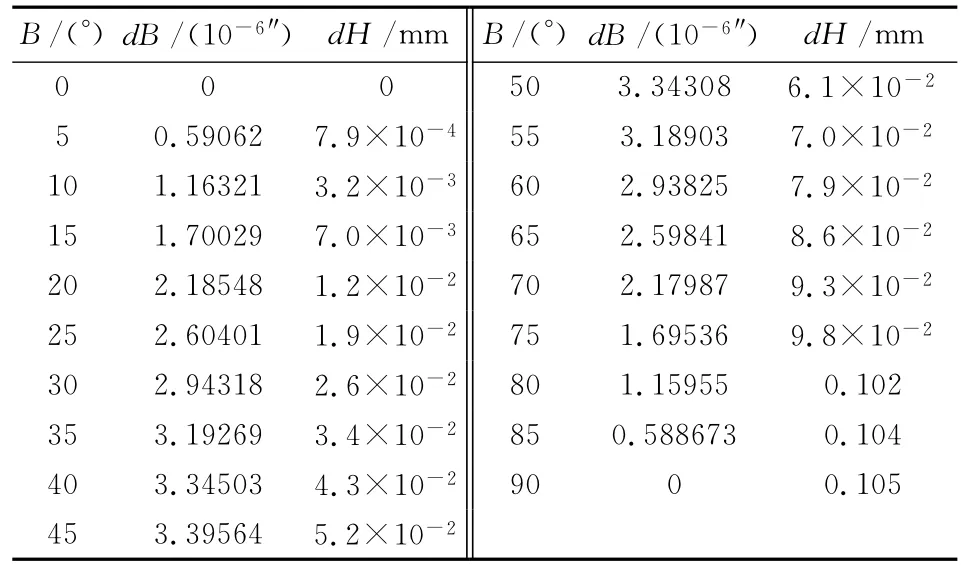
表3 CGCS2000与WGS84下不同纬度B 处的大地纬度和大地高的差异
由图2、图3并结合表3可知:同一点在CGCS2000和WGS84下大地纬度的差异呈正弦曲线变化,差异的绝对值在赤道和两极处最小,均为0,大约在45°N 和45°S处最大,约为3.4×10-6″,相当于0.105mm;同一点在CGCS2000和WGS84下大地高的差异呈反向余弦曲线变化,在赤道处最小,为0,在两极处最大,约为0.105mm。总的看来,在当前坐标测量精度为水平的情况下,同一点在CGCS2000和GRS80、WGS84坐标系内的大地坐标差异是可以忽略的。
3.2 两种椭球面上正常重力和正常重力垂直梯度的差异
CGCS2000和WGS84椭球面上正常重力值之间的差异dγ随大地纬度的变化如图4所示,正常重力垂直梯度值之间的差异dγ随大地纬度的变化如图5所示。按5°的纬度间隔,自赤道至北极的范围内,dγ和dγ的具体数值列于表4所示。
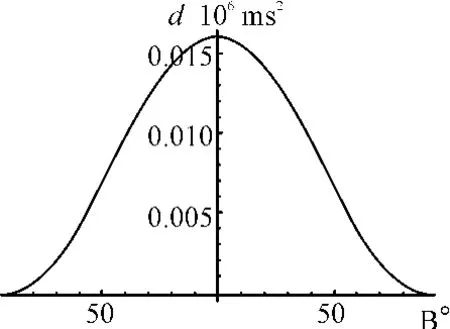
图4 CGCS2000和WGS84椭球面上正常重力的差异
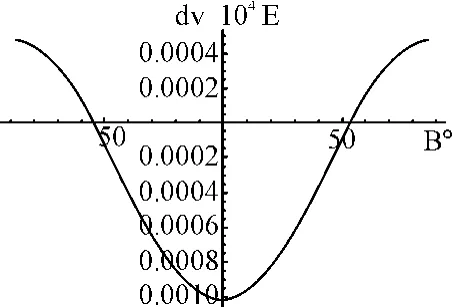
图5 CGCS2000与WGS84椭球面上正常重力垂直梯度差异
由图4、图5并结合表4可知:CGCS2000椭球面上的正常重力值比WGS84椭球面上的正常重力值稍大,二者差异在两极处最小,为0.00016×10-8ms-2,在赤道处最大,为0.016×10-8ms-2;CGCS2000和WGS84椭球面上正常重力垂直梯度值的差异的绝对值在赤道处最大,为0.001×10-4E(1E=10-9s-2),大约在55°N 和55°S处最小,为0E。总的看来,在当前重力和重力梯度测量精度分别为10-8ms-2和10-4E的情况下,CGCS2000和WGS84椭球面上的正常重力和正常重力垂直梯度的差异都是可以忽略的。
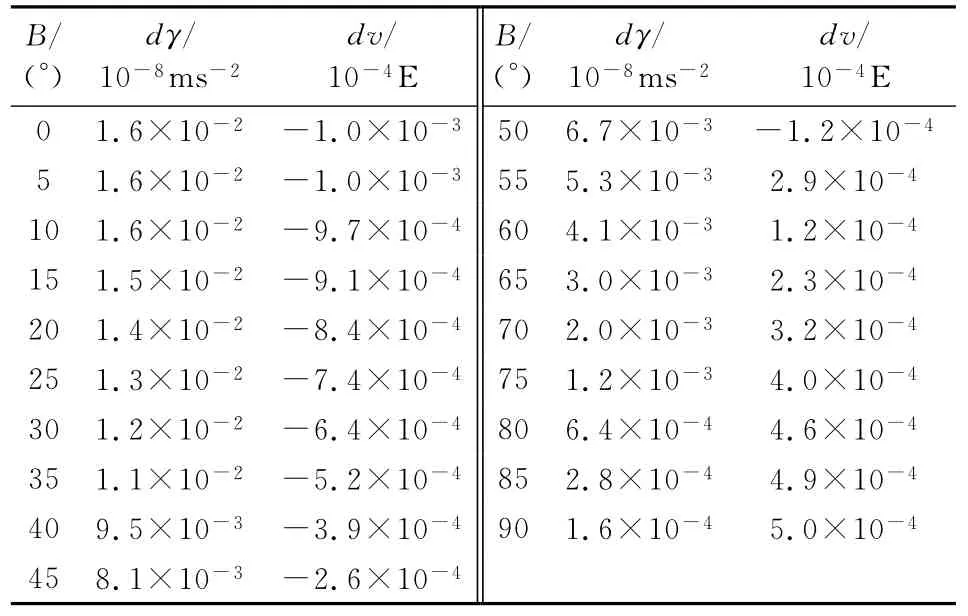
表4 CGCS2000和WGS84椭球面上不同纬度B 处的正常重力和正常重力垂直梯度的差异
4 结语
CGCS2000是我国采用的三维、高精度地心坐标系,是我国新一代大地基准,采用该基准可以最有效地利用空间技术,最大限度地取得空间技术所带来的好处。计算表明:同一点在CGCS2000和WGS84下大地纬度和大地高的最大差 异 分 别 为3.4×10-6″和0.105mm,CGCS2000 和WGS84椭球面上的正常重力值和正常重力垂直梯度值的最大差异分别为0.016×10-8ms-2和0.001×10-4E。在当前测量精度下,同一点在两种坐标系下大地坐标的差异以及两种椭球面上正常重力和正常重力垂直梯度的差异是可以忽略的。
[1]程鹏飞,文汉江,成英燕,等.2000国家大地坐标系与GRS80和WGS84的比较[J].测绘学报,2009,38(6):189-194.
[2]王瑞,李厚朴.基于地球椭球模型的符号形式的航迹计算法[J].测绘学报,2010,39(2):151-155.
[3]李厚朴,边少锋.扁球体水准面与水准椭球面形状差异的研究[J].测绘学报,2009,38(2):95-100.
[4]魏子卿.我国大地坐标系的换代问题[J].武汉大学学报·信息科学版,2003,28(2):138-143.
[5]杨元喜.中国大地坐标系建设主要进展[J].测绘通报,2005(1):6-9.
[6]陈俊勇.中国现代大地基准—中国大地坐标系统2000(CGCS2000)及其框架[J].测绘学报,2008,37(3):269-271.
[7]陈俊勇.与动态地球和信息时代相应的中国现代大地基准[J].大地测量与地球动力学,2008,28(4):1-5.
[8]陈俊勇.我国现代大地基准的思考[J].武汉大学学报·信息科学版,2002,27(5):441-444.
[9]杨元喜.2000中国大地坐标系[J].科学通报,2009,54(16):2271-2276.
[10]李厚朴.基于计算机代数系统的大地坐标系精密计算理论及其应用研究[D].武汉:海军工程大学,2010:177-190.

