基于GIS的华北地区降雨量空间变异性

刘益良，殷尧，朱庆杰，刘小光

(河北联合大学河北省地震工程研究中心，河北唐山 063009)

地统计学运用概率论和数理统计方法研究地理数据的空间分布规律，已经形成一个成熟的学科技术体系。而把地统计学与地理信息系统(GIS)整合在一起，构建一套完整的地统计分析工具，用ESRI的话说，是一次革命［1］。因为只有通过计算预测模型的统计误差，GIS才能够定量描述地理空间表面模型的质量。随着计算机技术与地质统计方法的迅速发展，一些包含地质统计模块的地理信息系统软件相继开发并得到了广泛的应用。有两个地理信息系统软件进行了这样的尝试，它们是ArcGIS和IDRISI。

随着我国经济的快速发展、人口的急剧膨胀以及生态环境的变化，使得社会对水资源的开发利用等一系列的问题更加关注，我国是水资源大国，对于水资源的研究显得尤为重要。降雨是水资源的重要来源之一，对工农业的生产建设和人们的日常生活都有着重大的意义。所谓降雨量，即从天空降落到地面上未经蒸发、渗透及流失的降水在水平面上聚集的水层深度。降雨具有间断性和空间变异性的特点，本文应用IDRISI软件的地统计模块对华北地区的48个气象站1971年至2000年的年降雨量进行空间变异性分析，研究华北地区降雨的空间分布规律。

1 地统计与空间变异性

1.1 地统计

地统计(Geostatistics)分析作为空间统计分析的一个主要内容，首先是由G.Matheron于1962提出的，是以区域化变量理论为基础，以变异函数为主要工具，研究那些在空间分布上既有随机性又有结构性，或空间相关性和依赖性的科学。地质统计学区别于经典统计学的最大特点即是:地质统计学既考虑到样本值的大小，又重视样本空间位置及样本间的距离，弥补了经典统计学忽略空间方位的缺陷。地统计分析理论基础包括前提假设、区域化变量、变异分析和空间估值［2］。

1.2 空间变异性

在统计学中，协方差函数和相关系数是测量两个随机变量相似性和差异性的常用工具。在地理学中，一个地理要素的观测值在两个较近位置间的差比较远位置间要小，地统计学应用了这两个领域的理论和方法，用数学工具来计算和表达地理空间的相似性和差异性，即空间依赖性。空间相似性即地理上的连续性(spatial continuity)，是地理现象或特征沿一定方向和距离，其属性以及表达属性的测量值没有或很少变化的一种分布模式。差异性则相反，它在数学上的表达，特称空间变异性(spatial variability)。空间变异指研究对象在空间上的变化，它是地质统计学研究的基本问题。

空间连续性或空间变化性分布现象的地统计学描述方法有很多，半方差函数运算(semi variogram calculation)是使用最多的一类，它计算采样数据成员间在指定的距离间隔和方向上平均的差异程度［3］。

2 克里金法

上世纪50年代初期，南非地质学家、矿业工程师克里金(D.G.Krige)［4］在矿山工作时观察到金属的分布在空间上并非是纯随机的，而是在空间上具有相互联系性。他于1952年提出克里金法，是一种无偏的最小误差的储量计算方法。该方法按照样品与待估块段的相对空间位置和相关程度来计算块段品位及储量，并使估计误差为最小。

法国巴黎矿业学院马特隆教授［5］(G.Matheron)对克里金提出的方法进行研究，认为克里金法是在考虑了矿化空间分布特征的基础上，合理地改进了统计学，是一种传统储量计算方法与统计学方法高度结合起来的新方法。同时为了解决具有二重性(结构性与随机性)的地质变量的条件下使用统计方法的问题，马特隆教授于1962年在经过深入探讨和实践之后，提出了区域化变量(Regionalized Variable)的概念，从而创立了地质统计学(Geostatistics)。根据地质统计学理论，地质特征可以用区域化变量的空间分布特征来表征。而研究区域化变量的空间分布特征的主要数学工具是变差函数(Variogram)或半方差函数(Semivariogram)，二者只是在定义上相差常数系数1/2，并无本质区别。

2.1 半方差函数

当定义了采样数据对(xi，xi+h)是在指定的距离间隔lag内的数据点对集合中空间距离为h的样本，z(x)，z(x+h)是随机变量z在x，x+h处的采样点值，同时假设两点之间的方差只与距离h有关，区域性变量理论的两个内在假设条件是差异的稳定性和可变性，一旦结构性成分确定后［6］，剩余的差异变化属于同质变化，不同位置间的差异仅是距离的函数，定义半方差函数为

式中，n为距离为h的样本对的数目，采样间隔h也叫步长。半变差函数(semivariogram)是IDRISI中采用的方差函数运算(variogram calculation)的一种统计量，属于空间变化性统计描述方法。对应于h的γ(h)的图被称为半方差图。

2.2 克里金方程

式中，λi是赋予观测值z(xi)的权重，表示各个观测值z(xi)对估计值的贡献。克里金是根据无偏估计和方差最小来确定加权系数λi的，即

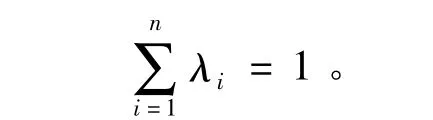
3 华北降雨量变异性分析

3.1 华北地区概况

我国华北地区的地理范围有多种说法，而且现在还没有对华北地区进行明确的定义。本文所指的华北地区仅是从气象预报的角度考虑，是指位于中国北部的区域，中国蒙古边境线以南，秦岭淮河线以北，西邻青藏高原，东濒渤海与东北地区的中国广大区域。位于北纬34°～53°，东经97°～125°之间，包括北京市、天津市、河北省、山西省和内蒙古自治区。

华北地区地势西北高、东南低，山地及山前冲、洪积平原是两大基本地貌单元。所跨的经纬度比较广，地貌多样，地形地势复杂，区域气候空间变异性明显。北部内蒙古属典型的中温带季风气候，具有降水量少而不匀、寒暑变化剧烈的显著特点。冬季漫长而寒冷，多数地区冷季长达5个月到半年之久。其中1月份最冷，月平均气温从南向北由零下10℃递减到零下32℃，夏季温热而短暂，多数地区仅有一至两个月，部分地区无夏季。最热月份在7月，月平均气温在16℃至27℃之间，最高气温为36℃至43℃。气温变化剧烈，冷暖悬殊甚大。降水量受地形和海洋远近的影响，自东向西由500毫米递减为50毫米左右。蒸发量则相反，自西向东由3000毫米递减到1000毫米左右。与之相应的气候带呈带状分布，从东向西由湿润、半湿润区逐步过渡到半干旱、干旱区。降水量空间变异性是根据实际观测的降水资料，分析降水量的空间变异性。

3.2 数据处理

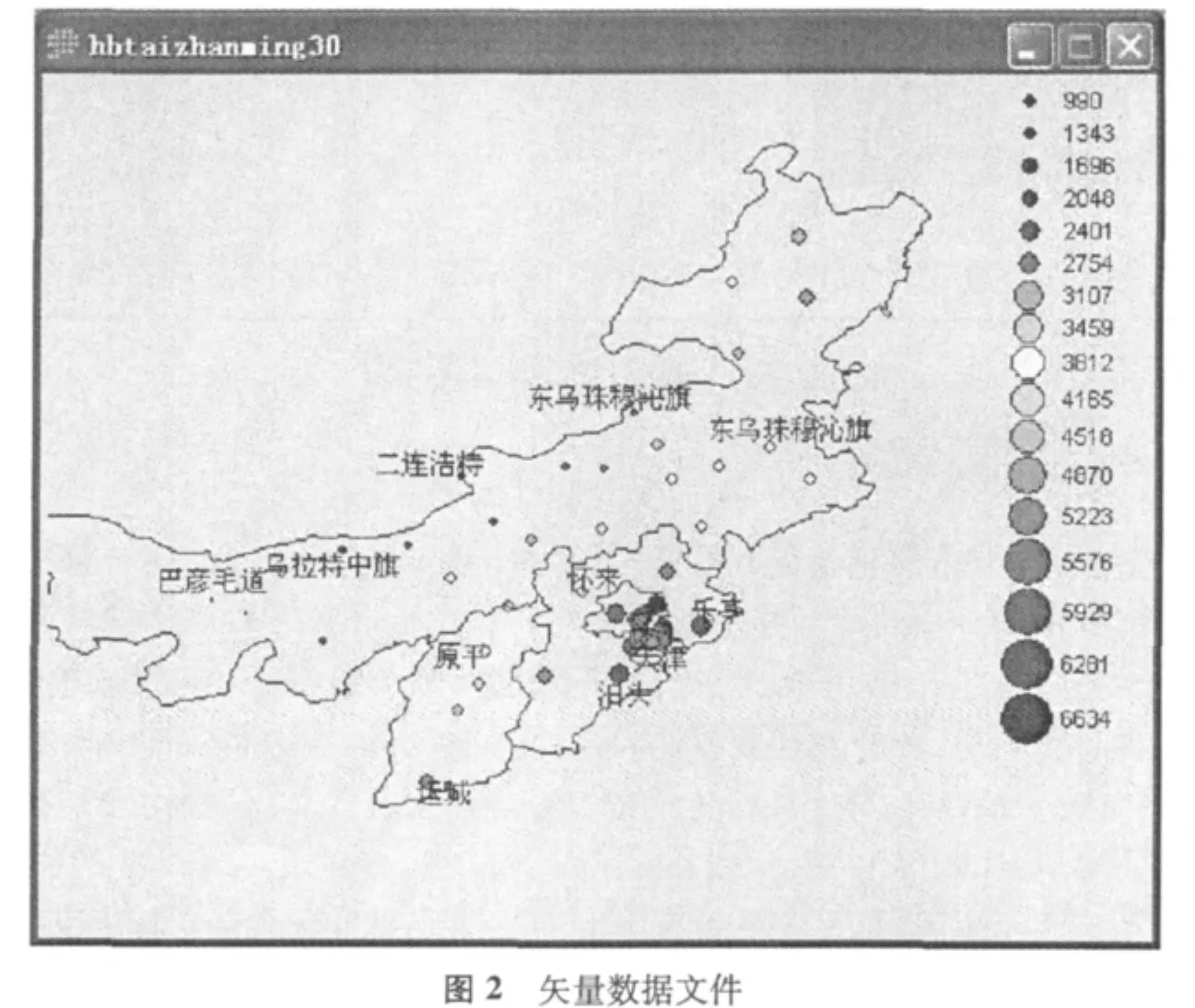
选取华北地区48个气象站从1971年至2000年30年的年均降雨量进行分析［7-8］，首先将这些气象站的名称、经度、纬度、高程、降雨量等数据存入Excel文档，然后将这些数据导入IDRISI数据库，如图1所示。将数据库中的数据生成矢量数据文件rain.vct，如图2所示。图中的小圆点越大，表示此气象站的降雨量最大。使用属性特征查询工具可以来查询每个降雨量观测站的属性数值。

2.3 半方差表面图

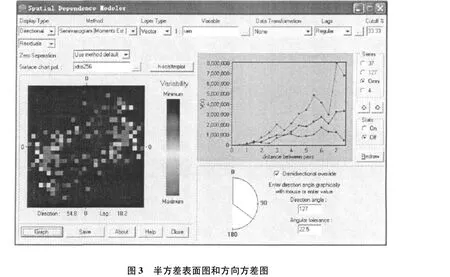
半方差表面图代表了空间统计［9］，它是依据方差云图(variogram cloud)得到的。方差云图是将每个采样数据点与其他采样数据点匹配并得到每个结果对的变差函数值制图的结果。根据其分离矢量，即分离的距离和分离方向定位半方差函数值，然后显示结果。在云图上叠加栅格，平均每个单元的云值创建一个栅格半方差表面图。在IDRISI软件地统计模块中打开空间依赖性建模器，将数据处理时生成的rain作为输入矢量变量(Variable)文件，显示类型应设置为表面类型，生成半方差表面图。由于采样点数比较少，半方差表面图不能明显看出降雨的连续性，改变步长参数，将步长数目设置为15，步长宽度设置为0.5，再次生成表面图，如图3左半部分。

栅格中央的步长距离为零，从中央沿各个方向向外移动时步长距离增加，方向读度数从正北开始按顺时针计算。当使用IDRISI标准调色板，深蓝色的颜色代表低的变异函数值，或低的变化，而绿色的颜色代表的高可变性。请注意在表面图底部显示的是与表面图中心的方向以及步长的数目。从图3可以看出，一个深蓝色带状大约呈37度分布，即最大的连续性方向在37度左右。

2.4 方向方差图

鉴于样本数据比较少，为了更好地分析降雨量的变异性，我们需要从不同的角度考虑。现在，我们将改进我们的分析方法，使用方向性图向不同的方向伸长。将显示类型有表面改变为方向性，方向角度设置为37度，绘制方向方差图。然后将方向角度改为127度，绘制127度方向方差图。选取全方位选项，绘制全方位图，如图3右半部分。

2.5 空间变异性分析

IDRISI探索空间变异性主要依靠观察半方差表面图(semivariogram surface)［3］。通过输入不同的步长宽度(lag width)和步长数(number of lags)，半方差表面图上清晰地显示出沿某些方向表示方差值的颜色的均一性，即可判定数据中存在方向性差异，IDRISI的点数据图层实现分级符号和分级彩色结合显示，结合图层的点位符号色彩分布和方差表面图来确定数据方向相关性的长轴方向(majorrange)和短轴方向(minor range)。同时在方向方差图上，可同时显示4个方向的方差点系列。本文只绘制了37度，127度和全方位的这三个方向的系列。

从图3可以注意到，37度系列随着间隔距离的增加连续性变化最低。在与其正交的127度方向，使用相同的步长间距，变异性却增加迅速。全方位的系列类似是所有方向的平均，因此，在这个例子中它位于两个系列之间。表面图和方向图的比较是合乎逻辑的。37度和127度系列揭示了在方向上的差异程度，即各向异性程度。

3 结论

通过上述分析可以得出华北地区降雨量的分布规律，在地图上以正北方向为0度，按顺时针计算，在127度方向上降雨量变异性最大。在同一条37度斜线附近气象站的降雨量变化很小。从图2可以看出，从东南沿海的天津、沧州、乐亭一带，越向西北内陆地区降雨量越少。使用软件分析得到的结果与实际情况相似，可见使用IDRISI软件可以简便、快捷、准确地对某一数据进行空间变异性分析，省去了大量的手工计算工作。我们此次应用IDRISI软件对华北地区1971年至2000年年均降雨量进行变异性分异，是对雨量变异规律探讨的一个新的尝试，从而使雨量变异规律的研究有了进一步的深入。本文仅使用了空间依赖性建模进行空间变异性分析，今后还可以使用模型拟合模块可视化地模拟一模型来描述数据的空间变化特征，使用克里金插值形成一连续表面。

［1］David Hollingsworth.The Workflow Reference Mode 1 Issue 1.1［M］.The Workflow Management Coalition Specification，1995-01.

［2］静，何必，李海涛.ArcGIS 9.3 Desktop地理信息系统应用教程［M］.北京:清华大学出版社，2011，02.

［3］王茯泉.地统计分析在ArcGIS和IDRISI中实现特点的讨论［J］.计算机工程与应用，2006，42(15):210-215.

［4］Journel A G，Huijbregts C J.Mining Geostatistics［M］.Academic Press，New York.1978.

［5］孙洪泉.地质统计学及其应用［M］.北京:中国矿业大学出版社，1990.

［6］邬伦.地理信息系统原理、方法和应用［M］.北京:科学出版社，2001.

［7］中国气象局.中国气象科学数据共享服务网:中国地面国际交换站气候标准值年值数据集(1971-2000).［EB/OL］.［2012-3-20］.http://www.cma.gov.cn/2011qxfw/2011qsjgx/index.htm.

［8］天津政务网.天津史志［EB/OL］.［2012-3-20］.http://www.tj.gov.cn/tblm/tj_sz/200709/t20 070921_22670.htm.

［9］刘光，贺小飞.地理信息系统实习教程［M］.北京:清华大学出版社，2003，01.