双向张拉索-混凝土结构自振特性

裴英超，秦乃兵，刘俊英

(河北联合大学建筑工程学院，河北唐山 063009)

0 引言

随着国家建筑技术水平的提升，大跨度结构将越来越受青睐，索-混凝土组合结构作为一种新型杂交结构，可以使得不同材料充分发挥其各自的优异特性。随着改革开放取得成功，建筑领域迅猛发展，促成了更多大跨结构的建成。目前，国内外研究较多的结构多为拉索拱结构，索承网壳结构等，且多为单向张弦梁结构，其抗侧性与稳定性都远远不及双向张弦梁结构强。对双向张拉索-混凝土组合结构的研究更是少之又少。因此，考虑到这类结构比较柔，且阻尼比小，以及在建筑结构中的重要性和破坏带来的经济损失和社会影响，搞清结构的振动特性，避免强振作用下影响到结构的正常使用及安全是非常具有现实意义的

本文利用ANSYS有限元软件对双向张拉索-混凝土组合结构进行模态分析，通过清晰的动态图象，来描述结构在受到激励时的表现，详细讨论了该结构的动力特性。

1 基本理论

1.1 结构动力学基本方程

由达朗贝尔原理可知，任意一个振动系统的平衡方程都可用下式来表示:

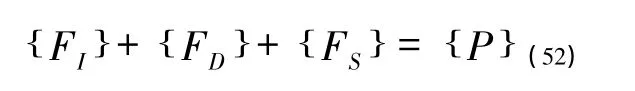
式中:

{FI}—结构的惯性力向量;

{FD}—结构的阻尼力向量;

{FS}—结构的弹性力向量;

{P}—外荷载向量。

其中将惯性力和弹性力向量用含有加速度与位移的向量表示为:

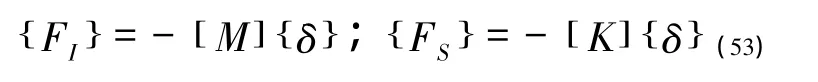
若采用粘滞阻尼假设时，阻尼力与速度成正比，此时阻尼力向量可写成下列形式:

利用单元叠加法，将惯性力、阻尼力及弹性力叠加，可得结点位移方程为:

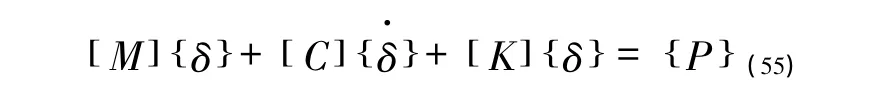
当既没有外荷载作用又忽略阻尼时，上式可记作:

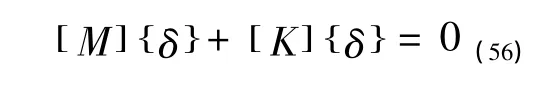
这就得到了系统的自由振动方程。

假设结构在自由振动时的位移为{δ}={A}cosωt代入后，可得如下方程:

该方程就是体系的特征值方程。通过求解，就可得到一个关于频率参数ω2的n次代数方程(其中n为体系自由度的次数)。将该方程的n个根按从小到大的次序依次排列，所形成的向量就称为频率向量[ω]，其中最小的频率称为基本频率或第一频率。

1.2 ANSYS动力学求解方法

ANSYS中提取模态的方法共有7种，它们是子空间迭代法、分块Lanczos法、PowerDyna法、矩阵缩减法、阻尼法、QR阻尼法和非对称法。其中，阻尼法和QR阻尼法不可用于求解方程。经大量研究发现，每一种方法都有其各自的优缺点和适用范围，因此选取适合的动力学求解方法，会使计算结果更加精准。

子空间法使用广义Jacobi迭代算法。计算精度很高，但速度较慢，尤其适用于求解大型结构的对称特征值问题。

由于结构的跨度较大，考虑到部分低阶频率和特征向量对结构动力响应的重要影响，故采用ANSYS中的子空间迭代法对双向张拉索-混凝土组合结构的自振特性进行了分析，提取了前30阶模态。

2 模态分析

结构的自振特性是其本身固有的极其重要的力学性能，又是衡量一个结构质量和刚度是否匹配、刚度是否合理的重要指标。此外，准确把握结构的自振特性还能避免与动力荷载发生共振的危险，因此，对双向张拉索-混凝土结构进行自振特性分析具有重要的意义。

2.1 模型简介

针对一两层一跨的双向张拉索-混凝土组合结构进行自振特性研究。该模型的各项参数如下:

混凝土梁长12 m，梁截面尺寸 0.4 m ×0.6 m;柱高4.2 m，截面尺寸0.8 m ×0.8 m;刚性杆0.5 m，索初始应变为 0.000 3，索截面面积 706.5 mm2，弹性模量 1.9e11Pa，泊松比 0.3，密度 7850 kg/m3;混凝土弹性模量 3e10 Pa，泊松比 0.3，密度 2500 kg/m3;刚性杆截面面积 1962.5 mm2，弹性模量 2e11 Pa，泊松比 0.3，密度7850 kg/m3。

依据以上参数建好的ANSYS模型如图1:

图1 双向张拉索-混凝土结构示意图

2.2 结果分析

通过ANSYS有限元分析软件，对上述索-混凝土结构进行模态分析。在结构动力分析中，对结构位移及内力影响较大的多为若干个低阶振型，所以根据结构的特性，研究了其前30阶振型来反映其动力特性，通过参数设置，得到了该结构前14阶振型的频率及振型图。其各阶频率如表1所示:

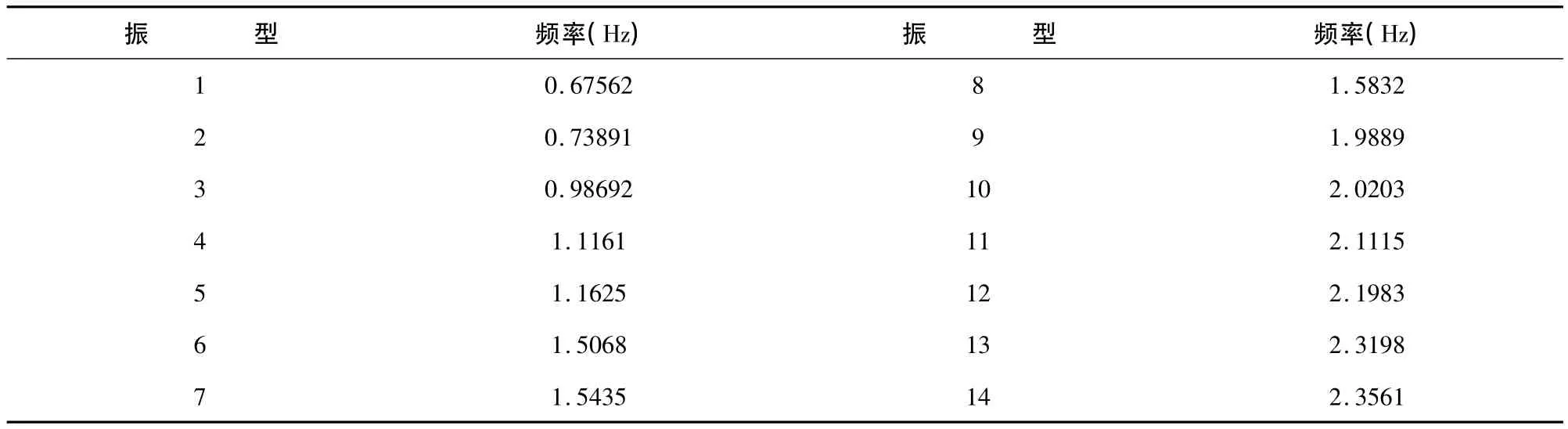
表1 结构自振频率

将所得到的14阶自振频率利用origin软件汇成柱状图，如图2:

图2 自振频率变化图

14阶振型图如图3:

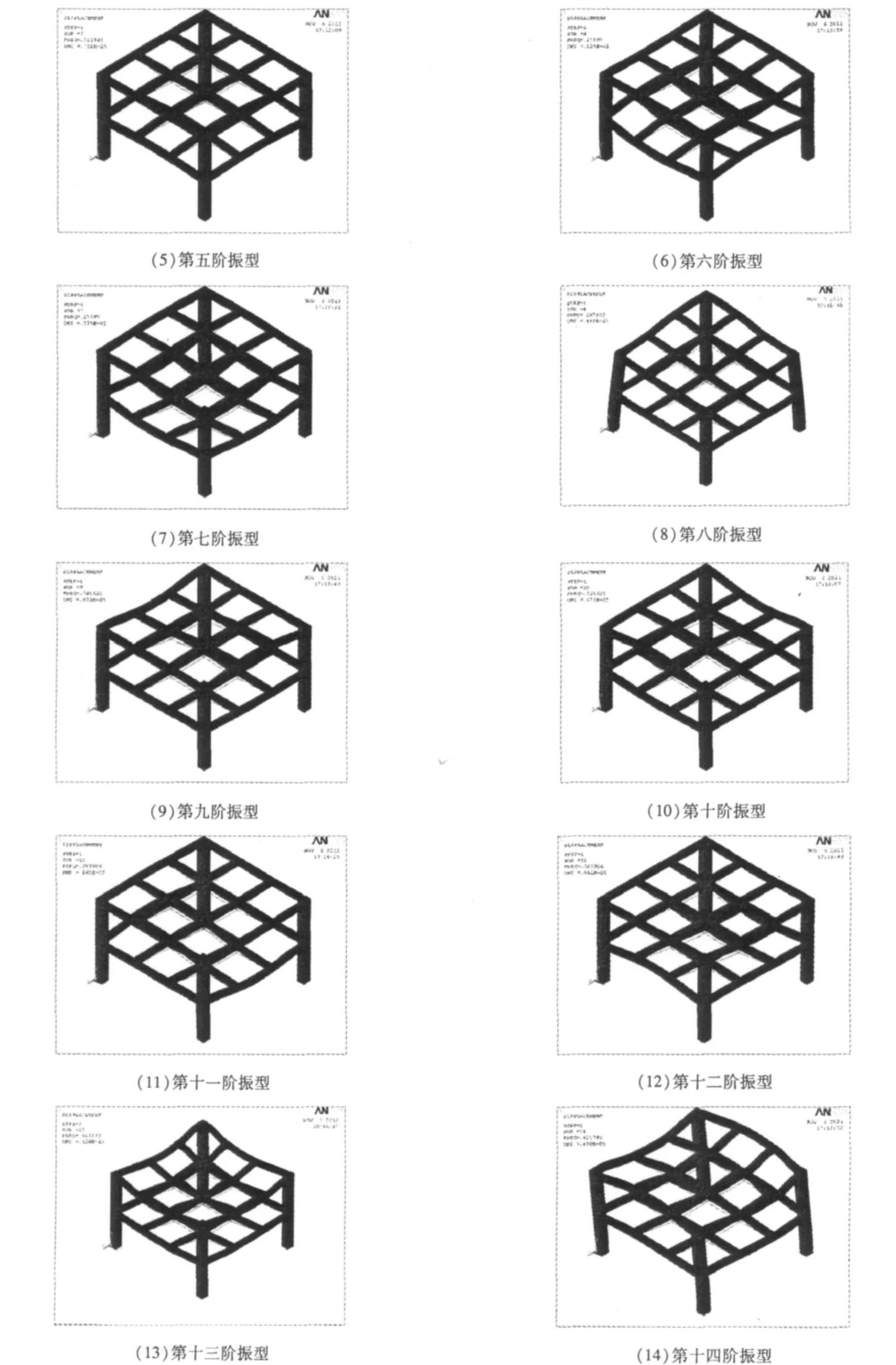
图3 振型图

由图表可知:

1)双向张拉索-混凝土结构的基频较小，表明总体刚度较弱，结构较柔。

2)结构频谱较密集，没有出现大的跳跃。这些频率呈阶梯状分布。在阶梯的分段处，结构的振型也呈现出较明显的变化。

3)双向张拉索-混凝土组合结构是一种形式较复杂的新型结构，由于索的作用，索应力的影响，其前很多阶振型表现出的仅为索的振动，而结构的主振型极有可能出现在高阶振型。因此，还需要研究各种动力参数对结构频率的影响。

3 各动力参数对自振特性的影响

为全面分析双向张拉索-混凝土组合结构的自振特性，本文试从索初始应力、索截面面积、梁的跨度、刚性杆高度等几个方面对结构的自振特性进行分析，进一步掌握其自振规律。

3.1 索初始应力的影响

在此分别选取初始应变为0.000 1，0.000 3，0.000 6三种情况。经过计算、分析，得到了不同情况下结构的自振频率，如表2所示。

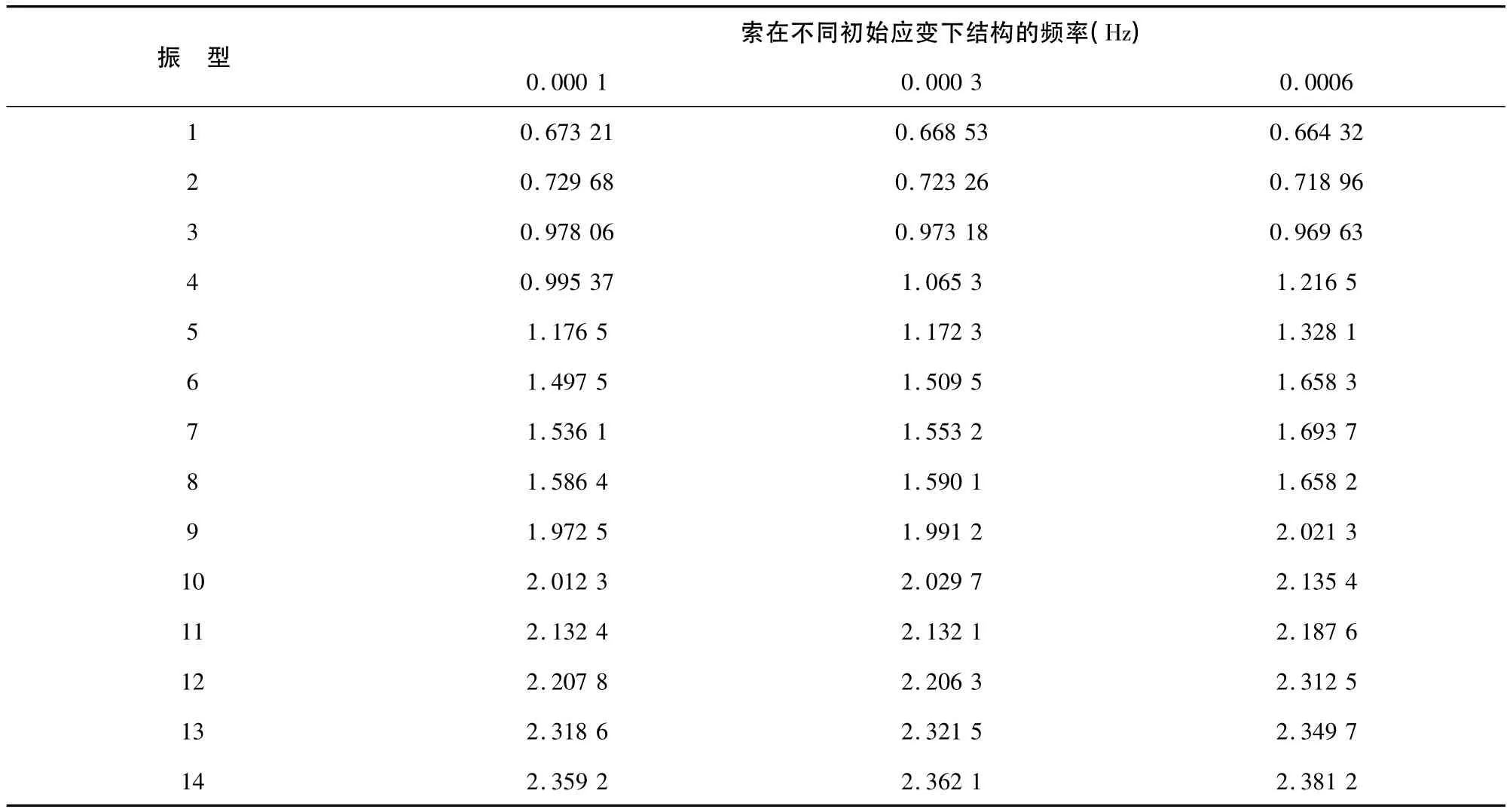
表2 索在不同初始应变下结构的频率

为了更加直观的显示，现将各振型相应的频率绘成柱状图，如图4所示。

图4 索初始应力对频率影响柱状图

根据上述数据及曲线图分析可知:双向张拉索-混凝土组合结构的基频受索初始应力的改变影响不大，随着索初始应力的增大而略有减小。从总体来看，结构的频率随着索初始应力的增大而增大，说明索的初始应力会改变结构的刚度。结构的频率曲线呈明显阶梯状变化。结构的频率曲线表明:随着索初始应力的变化，前几阶振型变化明显，而其后的振型差别较小，所以索初始应力的改变主要影响前几阶振型，对结构的刚度略有改变。

3.2 梁跨度对索-混凝土组合结构动力特性的影响

分别选取梁跨度为12 m，15 m，18 m三种情况。经过计算、分析，得到了不同情况下结构的自振频率，如表3所示:

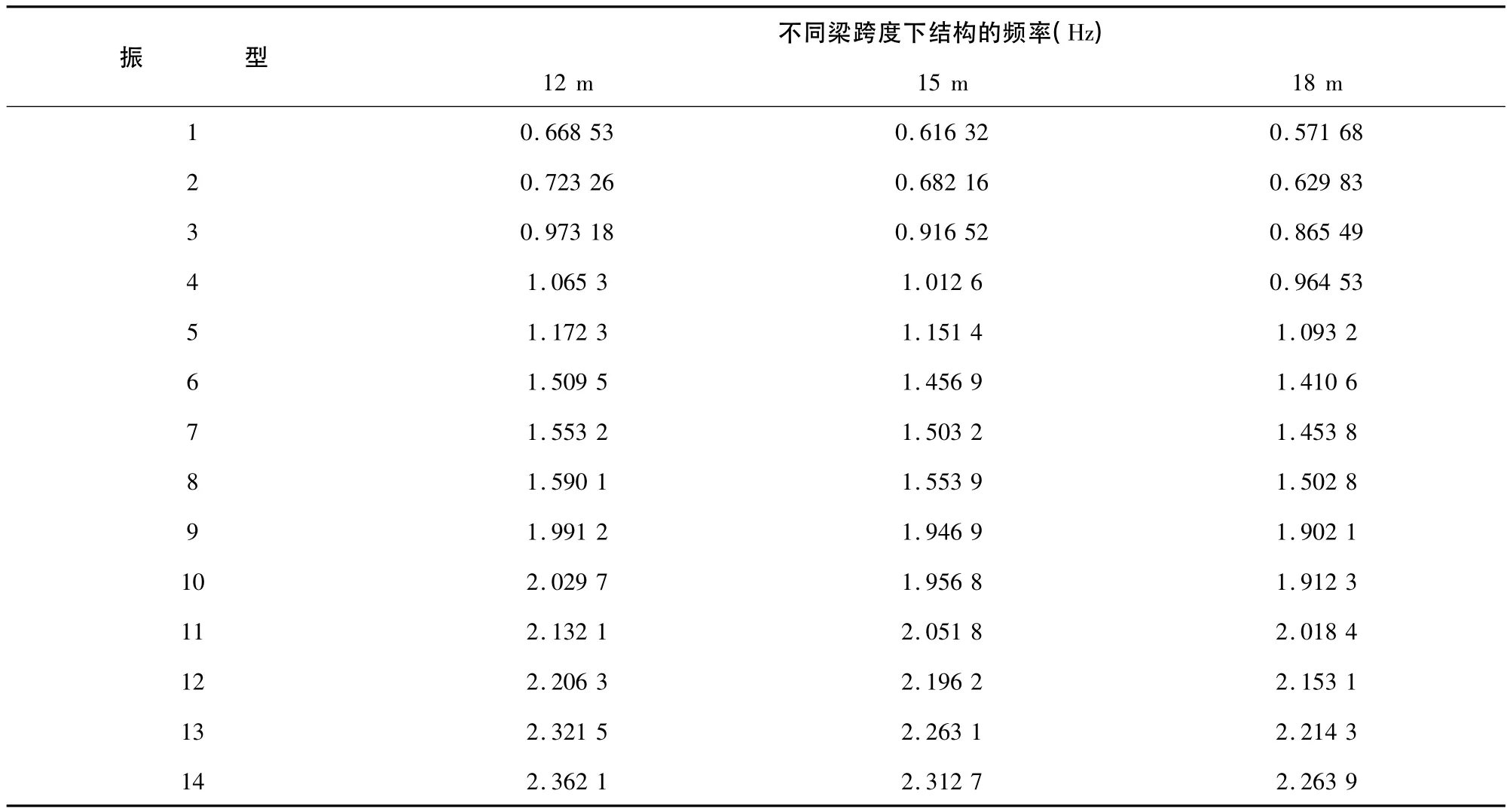
表3 索在不同梁跨度下结构的频率

绘成曲线如图5:

图5 梁跨度对频率影响图

据上述图表可知:双向张拉索-混凝土组合结构的第一频率随跨度的增大而减小。通过对所得的30阶自振频率进行分析可知，总体结构的自振频率随着跨度的增大而减小，结构频率曲线趋于缓和，说明结构变柔，刚度减弱。

3.3 刚性杆高度对索-混凝土组合结构动力特性的影响

为分析刚性杆高度对结构自振特性的影响，选取H=0.5 m，H=0.6 m，H=0.7 m三种情况。通过计算、分析，得到了不同情况下结构的自振频率，如表4所示:

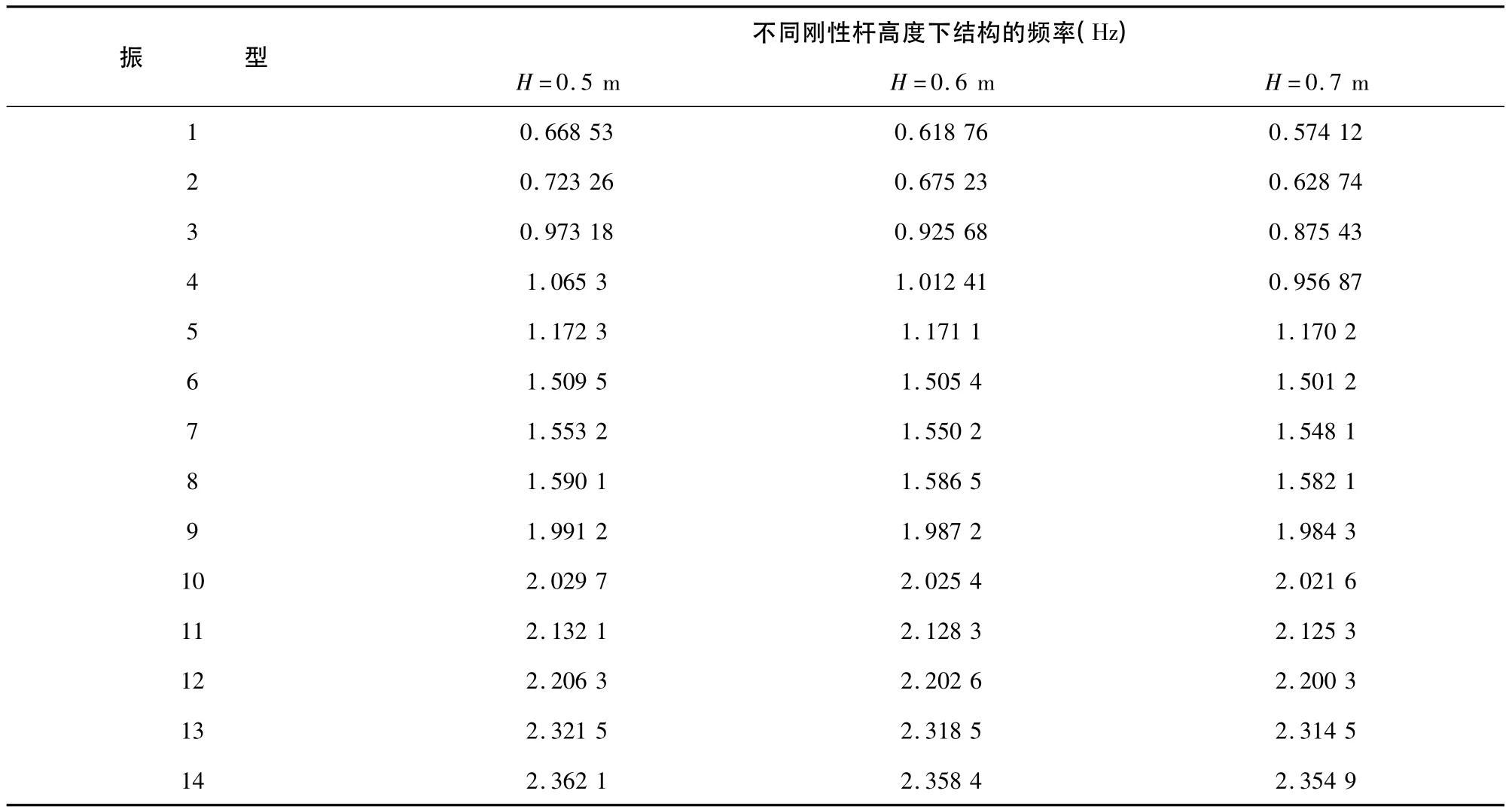
表4 索在不同刚性杆高度下结构的频率

绘成曲线如图6:

图6 刚性杆对频率影响图

通过对以上图表分析可知:双向张拉索-混凝土组合结构的基频随刚性杆高度的增加而减小，结构变柔。从总体来看，结构的频率随着刚性杆高度的增加而减小，但结构的自振频率变化不大，基本趋于一致。

4 小 结

本章利用ANSYS有限元分析软件中的子空间迭代法对双向张拉索-混凝土组合结构进行了模态分析，通过选取不同的参数，进行对比分析，系统地研究了双向张拉索-混凝土组合结构的自振特性。

1)双向张拉索-混凝土组合结构的基频较小，说明总体刚度较弱，结构较柔。结构频谱较密集，呈阶梯状分布，没有出现大的跳跃。阶梯分段处，振型呈现较明显的变化。

2)索初始应力增大，基频略有减小。结构的总体自振频率随着索初始应力的增大而增大，结构的刚度略有增加。

3)双向张拉索-混凝土组合结构的自振频率随着梁跨度的增大而减小，说明结构变柔，刚度减弱。

4)随着刚性杆高度的增加，结构的基频变小，总体频率变化不大，基本趋于一致，结构变柔。

［1］张毅刚.双向张弦梁结构和空间张弦结构的应用与发展［J］.工业建筑，2009.

［2］徐鹤山.ANSYS在建筑工程中的应用［M］.北京:机械工业出版社，2005.7.

［3］范思冬.索-混凝土组合梁的非线性分析［D］.唐山:河北理工大学，2010.

［4］刘俊英，秦乃兵，张雷.索-混凝土组合梁结构抗震性能研究［J］.建筑技术增刊，2011.

［5］徐常泽.双层弦张弦梁结构的动力特性及动力响应研究［D］.北京:北京工业大学，2007.