机组最优化问题的改进遗传算法

龚瑞昆，王新泽

(河北联合大学电气工程学院，河北唐山 063009)

0 引言

机组组合问题一直是编制调度计划首先要解决的问题。在确定了机组的启停状态，即某个时刻运行的机组群后，根据系统的负荷功率，在运行的机组间进行有功功率的最优分配即能量调度，从而使电力系统在满足系统安全约束、电能质量要求的条件下尽可能提高运行的经济性。

1 GA-ALOPEX算法

1.1 优化组合问题的数学模型

设机组调度周期为T小时，将之分为T个时段，机组或等效机组台数为G，各时段总负荷为PDT。

(1)目标函数

要求系统在T小时时段内各机组的总耗量为最小，目标函数可写为:

式中，Uit——机组i在t时段运行状态变量，仅设0，1两个值。Uit=0是表示运行;Pit——机组i在t时段的功率变量;Fi(Pit)——机组i的运行耗能;Si——机组i的启动耗量，它与停机时间的长短有关。

(2)功率平衡约束

(3)旋转备用约束

按系统总负荷的7%考虑旋转备用量，PRt=1.07PDt，则:

式中，PRt——系统旋转备用容量。

(4)机组容量约束

(5)机组启停次数约束

(6)机组最小连续停运和连续运行小时数约束

式中，T1、T2——分别为每台机组的最小连续停运和连续运行小时数

(7)功率速度约束

式中，τdi、τui——发电机组i输出功率的允许的最大下降速度和最大上升速度，PRti——机组i的旋转备用容量。

因此从数学上讲，机组优化组合就是在以上约束条件下求目标函数的极小值，这是一个有整数变量、连续变量及非线性函数的混合整数非线性规划问题。

1.2 ALOPEX 算法

由于遗传算法可以进行群体搜索策略和群体中个体信息交换，具有搜索不依赖于梯度信息、鲁棒性、全局收敛性、通用性强及无可微性的特点。在进入九十年代以后，遗传算法作为一种新的全局优化搜索方法，在规划设计、组合优化、机器学习、自适应控制和人工生命等方面得到了极为广泛的应用，尤其是它成功地解决了搜索方法难以处理的复杂的和非线形的问题。

尽管遗传算法以其鲁棒性、可并行处理性及高效率在许多领域中得到广泛的应用，但由于遗传算法本身爬山能力弱，容易“过早收敛”而使其在应用上受到限制。另外遗传算法在本质上属于无约束的优化算法，如何处理约束条件在很大程度上影响算法的效率，由于是随机的优化算法，不能保证得到全局最优解，计算量比较大，需要时间长。

(1)ALOPEX算法

由于传统的遗传算法本身爬山能力弱，容易“过早收敛”使其在应用上受到限制。为了使遗传算法的爬山能力得到提高，将遗传算法与ALOPEX(Algorithm of pattern extraction模式提取算法)算法结合起来，这样可以克服遗传算法爬山能力弱的缺点，并保持了遗传算法本身的优点，使算法的收敛速度和所获得的解的质量上都有所提高。

通常，一个实际的优化问题可以归结为求一个目标函数F(x1，x2，…，xn)的最大值或者最小值，其中x1，x2，…xn为自变量，N为变量维数，整个自变量集合可以表示为向量X。假设xi(t－1)和xi(t－2)分别为时刻(t－1)和(t－1)时自变量xi的值，那么，ALOPEX算法可以表述如下:

这里，δi(t)为步长，其取值δi的概率为pi(t)，取值为 －δ的概率为1－pi(t)。式(3)中a=1使得目标函数极小化，α=－1使得目标函数极大化。式(4)即为自变量的变化量和对应的目标函数值的变化量的相关性表达式，F(X(t－1))和F(X(t－2))分别为时刻(t－1)和(t－2)时对应的目标函数值。N为自变量的维数，M为一个预先定义的整数，为退火周期，当迭代次数为M的整数倍的时候，更新退火温度。

ALOPEX算法是一种利用单个权值变化与误差变化的局部相关量指导参数变化的算法，算法本身对目标函数没有任何要求。它利用提出的“噪声”来避免局部极值，用目标函数的变化与目标函数中各优化变量变化之间的相互关系来确定各优化变量的“走向”，使之适应于每次迭代，因而具有一定的“启发”意义。同时，所有优化变量在同一时刻被调整，可以实现并行计算。

ALOPEX算法具有以下几个特点:

(1)迭代反复进行，在每次迭代中每个自变量同时发生变化。

(2)自变量的变化取决于前两次迭代中其自身的变化和目标函数的变化，其变化受前两次迭代的启发，有利于加快收敛速度。

(3)自变量的变化方向以一定的概率确定，而该概率受温度及前两次迭代结果的控制。

(4)温度处于分母上，当其很大时，自变量向正负方向变化的概率各为一半，即温度较高时目标函数变化的随机性大，而温度较低时目标函数的变化受较优解的影响较大，其变化有一定的智能性。

1.3 ALOPEX算法的基本思想

在遗传算法的交叉算子与变异算子操作之后进行ALOPEX操作，即给予新个体—定的“噪声”，使其具有—定的爬坡能力，有利于遗传算法在搜索中跳出局部极值。在遗传算法进行的后期，种群中近似最优解占据绝大部分，使得交叉和变异操作很难跳出局部最优。由于个体间相似程度高，选取的两父代进行交叉和变异得到的子代与父代相差不大，致使收敛过程放慢，计算速度低。为了保证算法的全局收敛性，就要维持种群中个体的多样性，避免有效基因的丢失，另一方面为了加快收敛速度，就要使解群较快地向最优状态转移，这样又会减少群体，容易陷入局部极值点。在遗传算法中引进ALOPEX算法后，由于它在产生子代时可随机产生一定的“噪声”，使子代和父代相比有一定的差异，就会使种群具有一定的多样性，使算法具有一定的爬坡能力，收敛到全局最优，并能在一定程度上加快收敛速度。另外ALOPEX算法在搜索过程中利用前次自变量及其函数值的变化信息将有利于缩短搜索时间，其“噪声”是遗传代数的函数，随着收敛过程的进行逐步减小，有利于算法向全局最优前进。

1.4 ALOPEX算法嵌入GA的步骤

在种群按照交叉概率交叉操作得到两个新个体后，将其中一个父体设为t=2时刻的变量值，交叉产生的一个新个体设为t=1时刻的变量值，进行ALOPEX算法，得到t时刻的变量值，由所有t时刻的个体组成杂交种群。杂交种群再按照变异概率进行变异，变异后同样取父体为t=2时刻的变量值，变异产生的新个体设为t=1时刻的变量值，再进行ALOPEX算法而得到t时刻的变量值，由所有t时刻的个体组成变异种群。

2 算例

以本文献中算法为例，利用GA-ALOPEX算法对10台机组的系统进行机组组合优化算法，一个周期为24个时段，各机组的特性和各时段负荷见下表。

表1 机组特性数据

表2 负荷数据

用C++语言编写GA-ALOPEX算法程序对算例优化求解，分别选取不同的初始种群运算50次，其中的最优结果见表3(数据为0表示该时段该机组停机，不为0说明该机组的状态为运行)，GA-ALOPEX算法的收敛性见图1。

表3 最优组合的计算结果

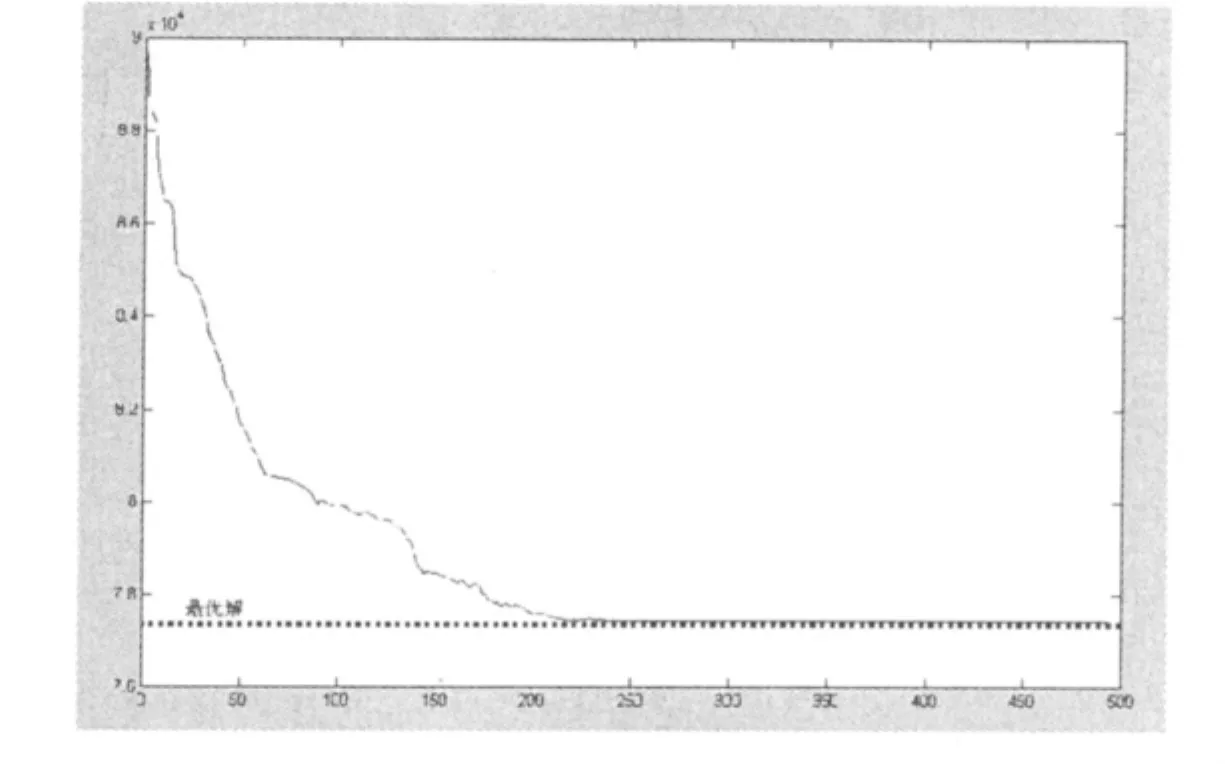
图1 GA-ALOPEX算法的收敛性

在该机组组合状态下的系统总耗量为77 438，文献［1］［3］都是采用同一个算例，总耗量分别是79807、81425。从算法的最优结果的对比可以看出，本文算法的局部搜索能力好于遗传算法和拉格朗日法。

图1表示的是在一次进化过程中每一代中的最好解和进化的代数之间的关系。从图中可以看出在开始最优值下降的很快，显示了算法的进化寻优能力的有效性;另外，算法进行到220代左右时就已经能够非常接近最优解，说明本算法具有很好的收敛性。此外，该算法的每一代的计算过程并不十分复杂，并能在很短的时间内就能得到问题的近似最优解，说明算法具有较高的计算效率。

在对50个不同的初始种群分别运行50次，得出的最好解为77 438，最差的解为77 529，两者之间的偏差只有0.12%，这说明本文算法具有很好的收敛稳定性，运用该算法进行求解机组组合问题，不需要多次计算进行对比，一次就可以得到很好的近似最优解。

3 结论

采用C++语言对算法进行编程，并应用于中小电力系统和扩大规模的电力系统，通过算例验证了该算法的计算效率和收敛稳定性。应用该方法编写机组优化程序，可以看到经过改进的遗传算法从理论上讲是合理的，在实例的计算上也取得了比较满意的效果。

［1］缪茜.基于目标优化的风光储能量策略研究［D］.成都:电子科技大学，2011.

［2］张建.基于GA-ALOPEX算法的机组优化组合的研究［D］.保定:华北电力大学，2005.

［3］郭成达.风光互补发电能量转换系统研究［D］.大连:大连理工大学，2008.

［4］商执一.风光柴蓄复合发电系统建模与仿真技术研究［D］.北京:北京交通大学，2010.

［5］A.G.Bhave.Hybrid solar-wind domestic power generating system-a case study［J］.Renewable energy，1999，17:355-258.

［6］G.C.Bakos.Technoeconomic assessment of a hybrid solar-wind installation for electrical energy saving ［J］.Energy and Buildings，2003，35:139-145.