H型钢阻尼器实验与数值仿真★
魏文财
(重庆交通大学土木建筑学院,重庆 400074)
全世界每年地震频发,而我国由于地理位置的原因更是地震的多发国,地震发生时间短,大的地震释放能量巨大,又由于其突发性,地震发生前很难准确预报,因此大的地震常造成重大的人员伤亡和财产损失,如唐山大地震,汶川大地震。为了保证人民的生命安全,必须对结构的抗震性能提出更高的要求。传统抗震结构体系是通过加强结构侧向刚度来满足抗震要求的,但这种被动抗震的方法对于大跨度结构及桥梁结构会造成严重的制约[1]。弹塑性软钢阻尼器具有强大的耗能能力,且滞回曲线越丰满,耗能能力越强,地震时软钢阻尼器率先进入塑性,消耗地震能量并延长结构的固有周期,保护了主体结构。软钢阻尼器还能与其他耗能器配合使用,抗震效果更好。软钢阻尼器比其他耗能器构造更简单,价格更低,耐久性更好。采用阻尼器来进行主动抗震是目前重要的发展趋势[2]。
目前国内外已研制出大量的阻尼器,其中软钢阻尼器由于具有稳定的滞回特性、良好的低周疲劳特性、受环境影响小等优点,而在实际工程中的应用极为广阔[2]。金属耗能器的耗能原理是通过屈服产生的滞回变形来实现的,其滞回曲线呈纺锤体形,加载频率和循环次数对其耗能性能影响小,工作性能稳定,耐久性能良好[3]。目前,软钢阻尼器有U形钢板阻尼器、三角形软钢阻尼器和X形软钢阻尼器[4]等型式。H型钢阻尼器相对于其他软钢阻尼器具有如下特点:构造更简单,屈服力更大,耗能效果更好。它通过软钢的屈服产生的塑性铰来消耗能量,它的结构形式能够很方便的安装和更换。
1 H型钢阻尼器实验设计
1.1 实验目的
1)获取热轧H型钢阻尼器滞回骨架曲线、屈服点及延性系数等。2)获得热轧H型钢阻尼器低周疲劳寿命及滞回耗能特性。3)获得热轧H型钢阻尼器塑性铰转动长度和转动能力。
1.2 材料选择
软钢具有很长的强化平台,在实际工程中钢阻尼器的材料一般采用软钢。因此本模型中阻尼器采用的钢材为Q235B级H W200×200×8×12型钢,其构造图见图1。
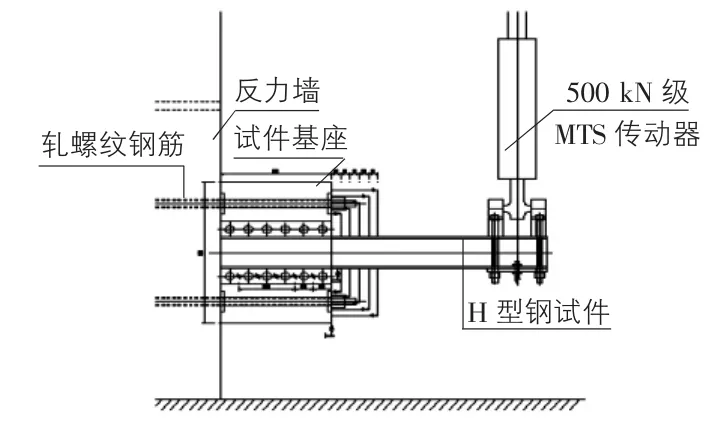
图1 H型钢耗能器构造
1.3 设计计算公式
根据结构力学,由H型钢阻尼器的原型可简化为一端固定,一端自由的梁模型,自由端作用力为F,计算简图见图2。

图2 H型钢耗能器计算简图
H型钢的本构各参数为:Q235的弹性模量为210 GPa,泊松比为0.3,屈服强度为260.13 MPa。采用结构力学中的方法求解图2的梁模型,剪力对H型钢的影响小,因此理论公式推导只考虑弯矩的作用。横截面的屈服弯矩My和塑性弯矩Mp可分别由以下公式求得:

其中,b,t,h分别为翼缘的宽度,厚度,上翼缘中心到下翼缘中心的高度;b1,t1,h1分别为上半部腹板的高度,厚度,上半部腹板到下半部腹板中心的高度。
相应的屈服力和塑性力由以下公式求得:
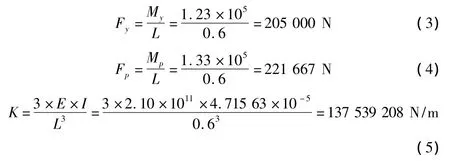
根据以上公式得到H型钢出现塑性时MTS要施加力222 kN。
1.4 实验工况设计
为了研究H型钢阻尼器的滞回耗能性能,对其进行两类工况的实验:工况Ⅰ为变幅位移循环加载实验;工况Ⅱ为等幅位移低周疲劳实验,见图3,图4。
实验工况Ⅰ为变幅位移循环加载,以热轧H型钢顶部推力作用线上的位移为控制指标,循环加载过程逐级增加位移幅值,直至试件根部塑性铰区断裂、试件破坏失效。每一级位移幅值循环3次,然后进入下一级位移幅值循环。循环位移比值取-1,波形取三角波,相邻位移峰值级差为H型钢顶部推力作用线上屈服位移理论值的约0.5倍,即0.4 mm,循环加载速率为0.5 Hz。

图3 实验工况Ⅰ 变幅位移循环加载波形示意图
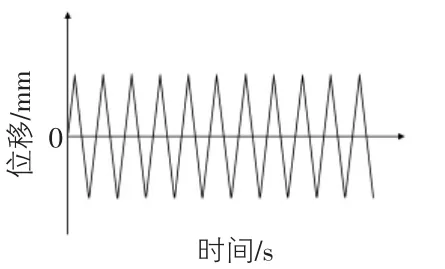
图4 实验工况Ⅱ 等幅位移循环加载波形示意图
实验工况Ⅱ为等幅位移循环加载,循环加载过程位移幅值不变,直至试件根部塑性铰区断裂、试件破坏失效。循环位移比值取-1,波形取三角波,位移幅值对应于该型试件型钢根部截面翼板边缘塑性应变幅值为0.04,即20.8mm,循环加载速率为0.5 Hz。
2 有限元仿真分析
2.1 计算结构模型及荷载
有限元计算采用ANSYS软件,Q235的弹性模量为210 GPa,泊松比为0.3,屈服强度为260.13 MPa,本构曲线见图5,混凝土基座的弹性模量为30 GPa,泊松比为0.2。Q235和混凝土基座的模拟单元为Solid186,它是具有塑性,应力刚化,大变形和大应变的20节点的实体单元。为了减少计算量,取对称结构的一半进行计算。对结构的对称面施加对称约束,对锚固孔洞施加固定约束,为了提取荷载反力的方便,对荷载面进行耦合约束,模型见图6。

图5 Q235的本构曲线

图6 模型实体图
2.2 初始刚度,位移延性系数,滞回曲线
在实际结构抗震建模计算中,对于滞回型阻尼器需要输入的重要参数就是弹性刚度和屈服荷载,因此首先加以介绍,实验与ANSYS计算得到的刚度图见图7,从图中可以看出,实验得到的刚度为30 kN/mm,ANSYS计算的为54.3 kN/mm。当H型钢出现塑性时MTS要施加力255 kN。ANSYS计算值为238 kN,与式(4)计算结果接近,进一步证明了在计算横截面的屈服弯矩My和塑性弯矩Mp时只考虑弯矩的作用是可行的。还可以看出ANSYS计算的屈服位移与实验值相差2 mm。这主要是因为在ANSYS仿真分析过程中,其边界条件认为是完全固接。而在试验中阻尼器的端部是通过螺栓连接,因此在阻尼器端部达不到完全固接的状态,这使阻尼器的刚度降低,因此要加以修正。而且,试验时存在摩擦力,从而造成加载时试验结果与有限元仿真结果的差异,该差异也表现在试验的屈服力比有限元仿真结果大,另一方面,ANSYS模型的本构曲线与实际的也有一些差距。尽管有差距,但由于阻尼器的弹性位移较小,以上偏差不会对阻尼器的耗能效果产生较大影响,即理论分析与试验结果在大位移下的滞回环面积基本相等。
根据等能量原理可以得到计算延性系数的简化形式,屈服荷载为 122.6 kN,位移延性系数为 12.91。

图7 H型钢刚度
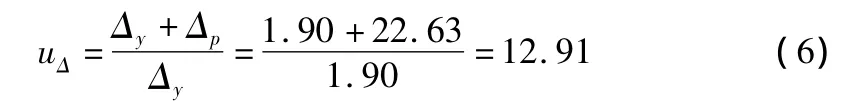
其中,Δy,Δp分别为H型钢翼缘外侧刚屈服时的位移和按照等能量原理计算的塑性位移。
由于常见实际的梁高,本文计算长度为0.6 m的情况,由于本文旨在说明其丰满的滞回曲线,以及软件计算的与实际的差距不大,因此仅列出最大位移为1 cm时的滞回曲线,见图8。另外为了减少计算的时间,在ANSYS计算滞回曲线时,不考虑混凝土基座的影响,即在H型钢与混凝土基座相交的面处零位移约束。
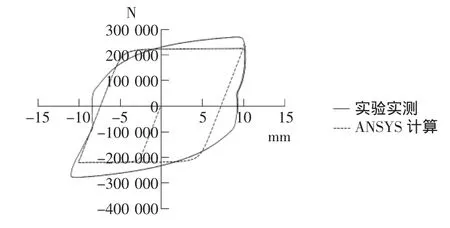
图8 最大位移为1 cm的滞回曲线
3 曲率分布
当H型钢潜在塑性铰处于弹性时,其曲率分布图为线性,如图9所示。

图9 H型钢处于弹性时潜在塑性铰曲率分布图
当潜在塑性铰处于塑性时,考虑低周疲劳的通用模型和疲劳试验结果有[4]:

其中,εm为截面外缘的应变;N为裂纹形成时的循环次数;E为弹性模量。取 E=2.1e5 MPa,N=60,则 εm=0.028 63。
截面最外边缘应变为0.002 863时的曲率分布图见图10。
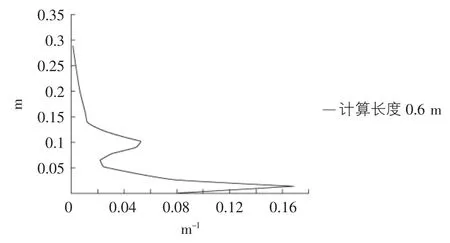
图10 H型钢处于塑性时潜在塑性铰曲率分布图
根据曲率分布图10,并结合等效塑性铰长度[5]的理念,即假定在底部附近存在一个长度为Lp的等塑性曲率段,在该段长度范围内,截面的塑性曲率恒等于墩底截面的最大塑性曲率φp,可得等效塑性铰长度为0.025 m,在计算分析中,塑性铰的力学模型是在塑性铰长度Lp的中间设置一弹塑性回转弹簧单元来模拟,铰上、下Lp/2区间按刚性构件计算,其回转弹簧的刚度根据H型钢结构变形等同的条件,即在图7中按MTS作用点得到的顶部水平位移与按弹塑性回转弹簧刚度计算得到的顶部水平位移一致。当最外边缘应变为0.002 863时,计算长度为0.6的阻尼器的位移为 9.9 mm,对应转动刚度为 0.016 851。
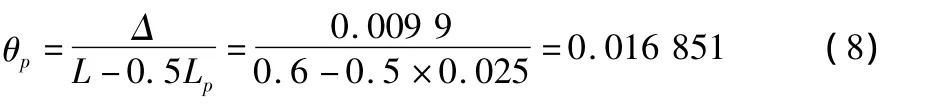
4 结语
通过有限元仿真分析和试验,其结果说明具有稳定的滞回特性、良好的低周疲劳特性的H型钢阻尼器是可以满足结构减震要求的,因此它可以取代传统的盖梁两侧的挡块,达到限位和耗能的目的,同时也为有限元软件计算其他尺寸的H型钢阻尼器的合理性提供了依据。并得到如下结论:1)仿真、试验分析与设计计算公式的屈服力值较吻合,由于阻尼器在应用实际桥梁之前均要通过屈服力的选取来选择阻尼器的尺寸,因此可以采用有限元仿真的方法来分析。2)通过塑性铰区曲率分布图可以看出在塑性铰区可以用一等效塑性铰来代替,并且计算出其转动刚度。
[1]周 云.金属耗能减震结构设计[M].武汉:武汉理工大学出版社,2006.
[2]章丛俊,李爱群,赵 明.软钢阻尼器耗能减震结构的研究与应用综述[J].工业建筑,2006,36(9):17-21.
[3]李爱群.工程结构减振控制[M].北京:中国建筑工业出版社,2005.
[4]吴 斌,欧进萍.软钢屈服耗能器的疲劳性能和设计准则[J].世界地震工程,1996(11):36-38.
[5]陈国兴,柳春光.工程结构抗震设计原理[M].第2版.北京:中国水利水电出版社,2009.

