转矩波动作用下弹簧减振器系统性能参数的多岛遗传算法优化
黄 鹏,左曙光,段向雷,胡 竞,李程祎
HUANG Peng, ZUO Shu-guang, DUAN Xiang-lei, HU Jing, LI Cheng-yi
(同济大学 新能源汽车工程中心,上海 201804)
0 引言
由电机引起的转矩波动越来越成为制约电动车平顺性发展的突出问题,为此一些研究学者从优化传递路径的角度着手,基于adams对悬架系统的性能参数进行优化,实现减弱转矩波动对车身平顺性的影响[1]。
然而在目前基于adams的优化仿真中,adams自带的响应面法优化算法与梯度下降法优化算法都存在着各自明显的缺陷。
根据相关学者的研究,由于响应面法的阶数较低,面对于工程实际问题,即使在响应面法所得结果拟合状况很好的情况下(调整系数R2与调整决定系数Radj2均大于0.9),依然不是模型全局最优解[2,3];而adams中另一种优化算法——梯度下降法,根据已有学者的研究成果,虽然具有较快的收敛速度,但其对于选取的初始值敏感,可能会收敛到一个局部的最优解[4]。
因此,现有的adams优化算法依然存在着精度不够高,鲁棒性较差等缺点,为了高精度的求解在转矩波动作用下弹簧减振器系统的最优性能参数,本文以adams与isight联合仿真优化为基础,在adams中建立包含“悬架-车轮-路面”的多体动力学模型,运用多岛遗传算法对弹簧-减振器系统(弹簧,减振器以及与其相连的衬套)的性能参数进行优化,克服了adams中优化算法所存在的缺陷,求解出性能参数在给定范围内的最优解,最终明显的削减了转矩波动对车身的影响。
1 悬架-轮胎-路面多体动力学模型的建立
为了优化弹簧减振器系统的性能参数,应在adams/view中建立准确的包含“悬架-轮胎-路面”的多体动力学模型。本文为排除前后悬架的耦合,只建立基于双横臂前悬架的多体动力学模型。
在多体模型中,车身被简化为在质心处的质量块,悬架与减振器通过弹簧衬套与车身,下横臂连接,轮胎模型采用高频柔性环轮胎模型ftire。建立起由18个刚体和66个自由度的悬架-轮胎-路面多体动力学模型,模型如图1所示。
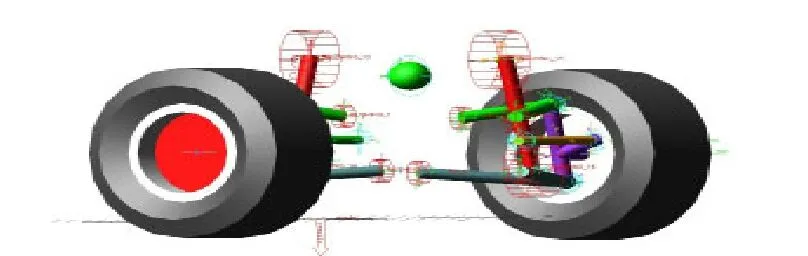
图1 建立的多体模型图
1.1 转矩波动模型
参考已有学者的研究成果[5],本文在多体模型中加入考虑磁阻转矩,永磁转矩和6i倍频转矩波动的转矩模型。
选取电机产生转矩波动的典型工作工况(100r/min转速,90N·m转矩下)作为多体模型的仿真工况,转矩的频域图如图2所示,从图中可以看出该驱动力矩在10Hz,20Hz,40Hz,60Hz,80Hz,100Hz和120Hz处存在明显的阶次特性。
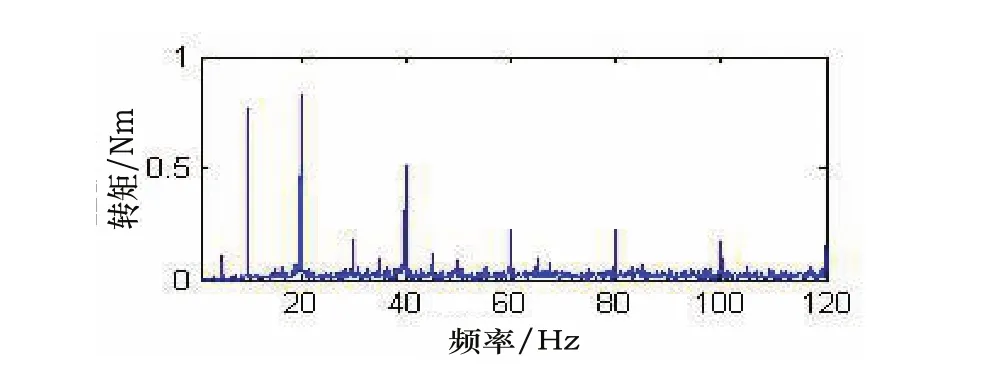
图2 转矩波动频域图
1.2 等效阻力:
为了使悬架能处于稳态行驶,在模型车身质心处添加等效阻力,其阻力大小为:

其中v为车身速度,k为综合阻力系数,
添加综合阻力后模型的速度曲线如图3所示。
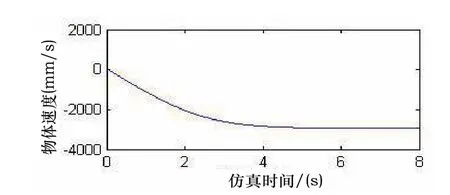
图3 车身速度随时间变化图
由图3可知在仿真时间5s后,车速稳定在2.93m/s,因此在5s~8s中,汽车处于符合转矩波动要求的稳态,下文对于信号的处理均截取5s~8s的信号。
2 基于多岛遗传算法的减振器-弹簧系统性能参数的优化
多岛遗传算法是建立在传统遗传算法基础上,它不同于传统遗传算法的特点是每个种群的个体被分成几个子群,这些子群被称为“岛”。传统遗传算法的所有操作,例如:选择,交叉,变异分别在每个岛上进行,每个岛上选定的个体定期地迁移到另外岛上,然后继续进行传统遗传算法操作。多岛遗传算法和传统遗传算法相邻两代之间的进化过程比较如图4所示[6]。
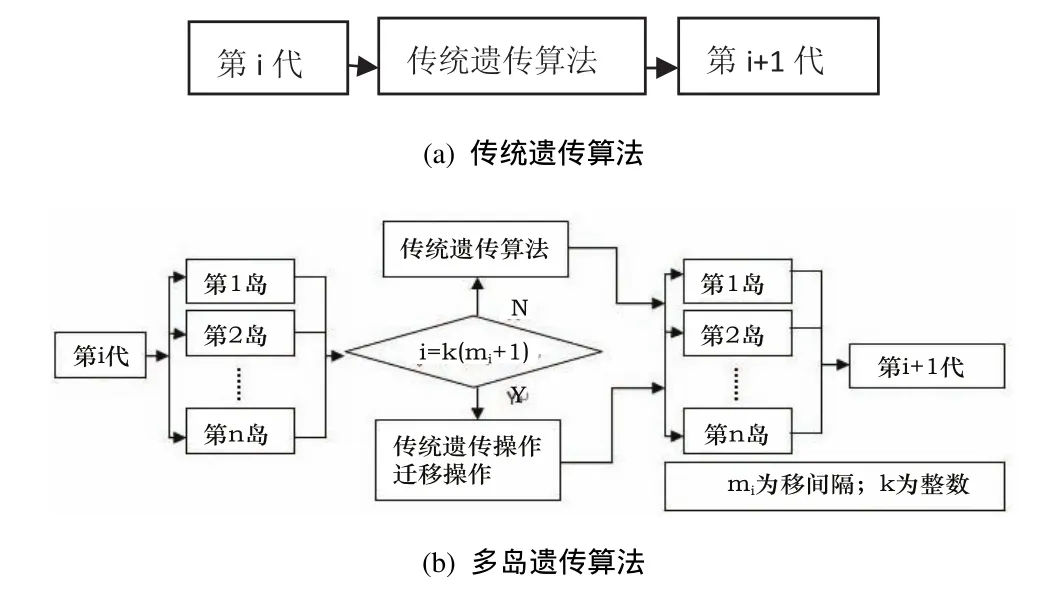
图4 传统遗传算法与多岛遗传算法相邻两代之间进化流程图
与响应面法和梯度下降法相比,多岛遗传算法有着求解精度高,鲁棒性强等优点,因此采用多岛遗传算法来对悬架系统的性能参数进行优化,可以有效的解决响应面法与梯度下降法自身的缺陷。
本文以isight与adams的联合仿真为基础,利用isight的simcode模块作为isight与adams的连接接口,以adams自身的优化参数作为遗传变量,以自行编写的运行adams/solver的脚本文件作为作为多岛遗传算法的评价函数,通过试凑法确定遗传策略参数,最终实现利用多岛遗传算法优化在转矩波动作用下弹簧-减振器系统的性能参数。采用多岛遗传算法一般包含四个步奏,本文各具体步奏如下:
1)优化策略参数的选取
多岛遗传算法优化策略参数对于遗传算法起着十分重要的作用,其中迁移率与迁移间隔是最为重要的两个参数,参考已有学者的研究经验[7]并采用试验试凑法确定迁移率与迁移间隔,最终在迁移率为0.3,迁移间隔为4的情况下优化实现成功收敛,其他优化策略参数的选取如下:子群数为10,岛屿数设计为10,进化代数为1000;选择概率0.8;交叉方式采用父代的加权平均值产生子代,交叉概率0.8;变异采用均匀变异方法,概率为0.1。
2)优化目标函数
汽车在转矩波动作用下的纵向振动与垂向振动均为其重要的振动表现形式[8],因此不可采取传统减振器设计的垂向加速度加权均方根值作为设计函数,而应采用纵向与垂向加速度的加权均方根值之和作为优化目标函数,由于人体对不同方向不同频率的敏感程度不同,参考ISO2631-1:1997的规定,结合所选轮胎和衰减转矩波动的目的设定优化目标函数,确定不同方向不同频率的加速度加权函数如式(2)~(4)所示,其垂向各频率段加权函数如式(2)所示,纵向各频率段加权函数如式(3)所示,纵向与垂向加速度总体加权函数如式(4)所示。

3)优化变量的选取与变化范围的确定
弹簧减振器系统的外部结构参数(如硬点位置),主要是由车辆的内部空间所决定,而真正影响车身平顺性的是弹簧减振器系统的性能参数(包含弹性元件的刚度与阻尼)[9]。因此本文选取弹簧,减振器以及弹簧减振器与车身和悬架连接处衬套的刚度阻尼值作为研究对象,设定各优化参数初始值与优化范围如表1所示。

表1 各优化参数变量及其变化范围
4)优化结果的评价
对adams模型进行多岛遗传算法优化,其中adams所执行的仿真是模型在平直路面上沿直线行驶,仿真时间为8s,仿真步长为0.001s,所得优化目标函数收敛趋势如图5所示。

图5 目标函数在遗传算法下的收敛曲线
由图5可知,在初始阶段,由于所取初始值的随意性,所得期望数据较为发散,经200代左右后,遗传算法找到局部最优解,之后由于多岛遗传算法所特有的“选择-交叉-变异-迁移”致使结果在一些遗传代出现明显的阶跃,但经过较短的遗传后再次收敛到某一局部最优解,在800代以后,所期望的函数值渐渐稳定在最优解,因此表明多岛遗传算法进行了全局的搜索,优化结果必然是全局最优解[10]。最终求得弹簧减振器系统的性能参数如表2所示,优化前后车身纵向,垂向加速度与整体加速度的加权均方根值如表3所示。
3 采用响应面法和梯度下降法与多岛遗传算法
分别采用响应面法与梯度下降法对弹簧减振器的性能参数在同样的变化范围内(参见表1)进行优化,其中响应面法的调整系数R2为0.974(一般性要求大于0.95),调整决定系数Radj2为0.953(一般性要求大于0.9),因此该响应面法对模型拟合精度很好,结果可靠[11]。响应面法与梯度下降法优化后的性能参数最终结果如表2所示,纵向,垂向加速度与整体加速度的加权均方根值如表3所示。

表2 各参数优化前后取值
4 结果分析
将三种优化后的弹簧减振器系统的性能参数分别导入adams再次进行仿真,得到优化前后的车身纵向与垂向加速度对比图,如图6、7所示,由图6、7可以看出经过多岛遗传算法优化后,汽车的纵向,垂向加速度在转矩波动引起的加速度振动幅值处都有明显的下降,对于车身的垂向与纵向加速度在0~120Hz频率段内都有一定程度的降低;整体来看,经过多岛遗传算法优化后车身的加速度加权平均值下降17.9%,整体平顺性有着显著的提高。因此采用多岛遗传算法对弹簧减振器系统的性能参数进行优化效果明显,可以有效的衰减转矩波动对车身加速度的影响。

图6 优化前与优化后纵向加速度对比图
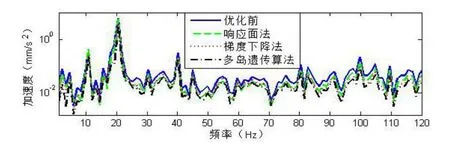
图7 优化前与优化后垂向加速度对比图
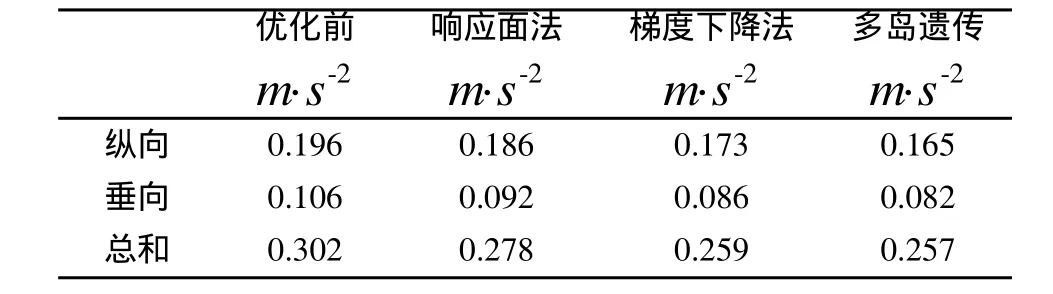
表3 经三种优化算法优化后三向加速度对比表
对比表2数据与遗传算法优化所得结果,可以发现经响应面法优化后的性能参数往往为取值范围的上下极值,这主要是由于响应面法阶数不高,自变量相对于优化目标呈现近似线性关系所致[12],结合表3所列结果不难发现响应面法所得结果与全局最优解依然有着不小的差距,因此响应面法即使在对模型拟合很好的情况下所得结果对于该系统依然不是全局最优解。
梯度下降法所取数值虽然不在范围上下限,但所得结果与遗传算法也存在一定的差异,结合汽车纵向与垂向加速度对比图(图6、7)与表3可知梯度下降法由于所选初值的原因最终收敛于局部最优解,这说明梯度下降法对于初始值较为敏感,容易收敛于局部最优解。
5 结论
1)弹簧减振器系统的性能参数对于整车平顺性的影响十分显著,通过合理的选取弹簧减振器系统的性能参数可以显著的提升整车的平顺性。
2)采用多岛遗传算法对悬架多体模型中的弹簧减振器系统进行优化设计,可以显著的减小转矩波动对整车的影响,车身的纵向与垂向振动加速度在0~120Hz范围内有效降低,整车加速降低17.9%。
3)采用多岛遗传算法对adams模型进行优化,相较于常用的响应面法与梯度下降法可更高精度,更高可靠性的求解模型全局最优解。
[1]李程祎,左曙光,段向雷.考虑转矩波动的电动汽车NVH性能参数优化[J].汽车工程,201335(4):303-306.
[2]刘成立,吕震宙.结构可靠性分析中考虑高次项修正的组合响应面法[J].航空学报,2006,27(4):594-599.
[3]潘雷,谷良贤.分块响应面法研究[J].计算机工程与应用,2009,45(19):37-39.
[4]刘皓明,K Mok T..李扬.等.基于遗传算法的UPFC模糊阻尼控制器参数优化及与梯度下降法的比较[J].电力自动化设备, 2005,25(11):5-10.
[5]马琮淦,左曙光,何吕昌,等.电动车永磁同步电机电磁转矩的解析计算[J].振动、测试与诊断,2012,32(5):756-761.
[6]杨海峰,韩晖,吴子燕.基于MIGA的结构模型修正及其应用[J].振动、测试与诊断,2012,32(2):261-266.
[7]陈曦,林涛,唐贤瑛.遗传算法的参数设计与性能研究[J].计算机工程与设计,2004, 25(8):1309-1310,1319.
[8]于增亮.轮毂电机驱动电动车悬架系统振动分析[D].上海:同济大学,2010.
[9]刘慧斌.Strut-Links型后悬架硬点及衬套刚度优化方法的研究[D].吉林大学,2011.
[10]石秀华,孟祥众,杜向党,等.基于多岛遗传算法的振动控制传感器优化配置[J].振动、测试与诊断,2008,28(1):62-65.
[11]董恩国,张蕾,申焱华,基于2阶响应面模型的汽车前轮定位参数设计研究[J].汽车技术,2007(11):22-25.
[12]王延克.基于响应面法的汽车悬架系统优化设计[D].成都:西南交通大学,2009.

