相邻双交叉口的三级模糊协调控制算法分析

杨 阳，余立建，胡丹龙

（西南交通大学 信息科学与技术学院，四川 成都 610031）

1 两相邻路口的交通模型

当城市干线上任意两个交叉口之间距离小于800m的时候，其中一个交叉口的运行状态必然受到其相邻交叉口运行状态影响，此时如果继续按照孤立交叉口的信号控制（点控）方法来控制交叉口的信号运行将难以有效提高整个交通干线的通行能力。因此，本文从相邻双交叉口协调控制的角度出发，来研究城市交通干线的通行能力。

从图1可以看出，每个交叉口有4个车辆运行方向，每个方向又有3个车道，这3个车道分别为左转、直行、右转车道，每个车道有2个感应线圈。上游感应线圈用来测量每1s内进入该方向的车辆数，下游感应线圈用来测量该方向为绿灯时每1s内离开该方向的车辆数。

图1 相邻两路口车辆行驶几何模型

图2表示信号控制的相位分布图，信号采用四相位控制，即东西直行、东西双左转、南北直行、南北双左转。右转车辆通过专用车道随时疏散，不设单独相位。信号控制系统采用定相序控制，即相位按照一定的顺序进行更替变换，本文采用的相位变化先后顺序为东西直行、东西双左转、南北直行、南北双左转。

图2 信号控制的4种相位描述

所有车道按照既定的规则进行统一编号，并设在t－Δt时段第i号交叉口第j个车道驶入两交叉口中间路段的车辆数为Iij（t），该时段内从两交叉口中间路段驶向第i号交叉口第j个车道的车辆数为

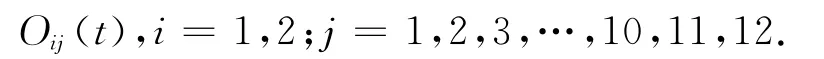
要实现相邻双交叉口之间的协调控制，最主要就是让相邻双交叉口之间拥有的车辆数量作为输入条件参与到单交叉口研究出来的模糊控制方法中去，使相邻双交叉口的运行状态关联起来。

设Q21（t），Q12（t）分别表示t时刻后交叉口2到交叉口1和交叉口1到交叉口2中间路段的车辆数，则有如下关系

其中

且

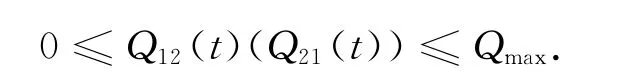
其中，Qmax为两交叉口之间路段能容纳的最大车辆数，等于两交叉口之间路段距离D与车辆长度L之比，Qmax＝D／L。

设Qi，j（t）为第i号交叉口第j车道在t时刻通过上下游感应线圈检测所拥有的车辆数。则

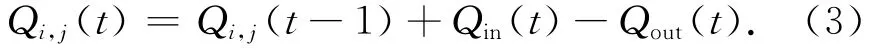
其中，Qin（t）为第t时刻内驶入该车道的车辆数，Qout（t）为第t时刻驶出该车道的车辆数。且0≤Qi，t（t）≤Q′max，其中Q′max为每车道2个感应线圈之间能容纳的最大车辆数，等于2个感应线圈之间路段距离C与车辆长度L之比，且Q′max＝C／L。

2 相邻双交叉口模糊协调控制算法介绍

关于2个相邻路口的协调控制算法，已有部分学者投入了大量的研究并且得出了较好的效果，有的也已经开始运用于城市干线的交通信号控制。提出一种新的协调控制算法，即三级模糊协调控制方法，并通过此方法来实现相邻双交叉口的协调控制。

本文通过仿真1200s的时间来得出在此期间内每辆车的平均延误，其中每个相位的最少绿灯时间为15s，最长绿灯时间为60s，设置两交叉口间中间路段在初始情况下拥有的车辆数为50辆。

Step1：初始化，置初始时间time＝0，两交叉口的相位都为相位1（东西直行相位），并且指定两交叉口各相位的最小绿灯时间Tmin和最大绿灯时间Tmax。

Step2：先给两交叉口初始相位的最小绿灯时间Tgreen＝Tmin。

Step3：在Tgreen时间末，计算两交叉口当前绿灯相位各车道上的上下游感应线圈间车辆数Q1g，Q2g，和下一红灯相位各车道上上下游感应线圈间车辆数Q1r，Q2r；并且计算此时绿灯相位在达到最小绿灯时间之后经过的绿灯时间t1g、t2g，下一红灯相位经过的红灯时间t1r、t2r；通过小波神经网络分析两交叉路口中间路段车辆数的历史数据而得出当前时刻中间路段车辆数Q21、Q12。

Step4：

第一级模糊控制：

输入Q1g和t1g，由模糊逻辑推理得出交叉口1的绿灯相位繁忙度U1g；

输入Q1r和t1r，由模糊逻辑推理得出交叉口1的红灯相位紧迫度U1r；

输入Q2g和t2g，由模糊逻辑推理得出交叉口2的绿灯相位繁忙度U2g；

输入Q2r和t2r，由模糊逻辑推理得出交叉口2的红灯相位紧迫度U2r。

第二级模糊控制：

输入U1g和U1r，由模糊逻辑推理得出交叉口1相位切换值GT1；

输入U2g和U2r，由模糊逻辑推理得出交叉口2相位切换值GT2。

Step5：

第三级模糊控制：

对于交叉口1，输入GT1与Q21由模糊逻辑推理得出改进后的相位切换值GT11，输入GT1与Q12由模糊逻辑推理得出改进后的相位切换值GT12，最后通过计算GT11和GT12的平均值得到协调控制下交叉口1的相位切换值GT1；

同理，可以得出交叉口2在协调控制下的相位切换值GT2。

Step6：

如果仿真时间time＜1200：

对于交叉口1，如果GT1不满足切换相位条件：

Tgreen＋5≤Tmax，那么Tgreen＝Tgreen＋5，转至Step3；

Tgreen＋5＞Tmax，Tgreen＝Tmax，转至Step3；

如果GT1满足切换相位条件，那么该交叉口绿灯相位由当前绿灯相位切换到下一相位，并给切换后的绿灯相位置最小绿灯时间Tgreen＝Tmin，转至Step3；

同理，对于交叉口2，相位切换原则与交叉口1算法一样。

如果仿真时间time达到了1200s，转至Step7。

Step7：停止仿真，搜集数据，得出结论。

3 协调模糊控制器的设计

采用三级模糊协调控制算法，实现相邻双交叉口的协调控制。第一级模糊控制器根据Q1g，t1g，Q1r，t1r，Q2g，t2g，Q2r，t2r分别得出交叉口1绿灯相位繁忙度U1g和红灯相位紧迫度U1r以及交叉口2的绿灯相位繁忙度U2g和红灯相位紧迫度U2r。第二级模糊控制根据U1g，U1r，U2g，U2r分别得出交叉口1的相位切换值GT1和交叉口2的相位切换值GT2。第三级模糊协调控制器根据GT1，GT2，Q21，Q12分别得出交叉口1的协调控制下修正相位切换值GT1和交叉口2的协调控制下修正相位切换值GT2。

下面将以1号交叉口为例，分别介绍各级模糊控制器的设计。

3.1 各级模糊控制器输入参数的隶属度函数

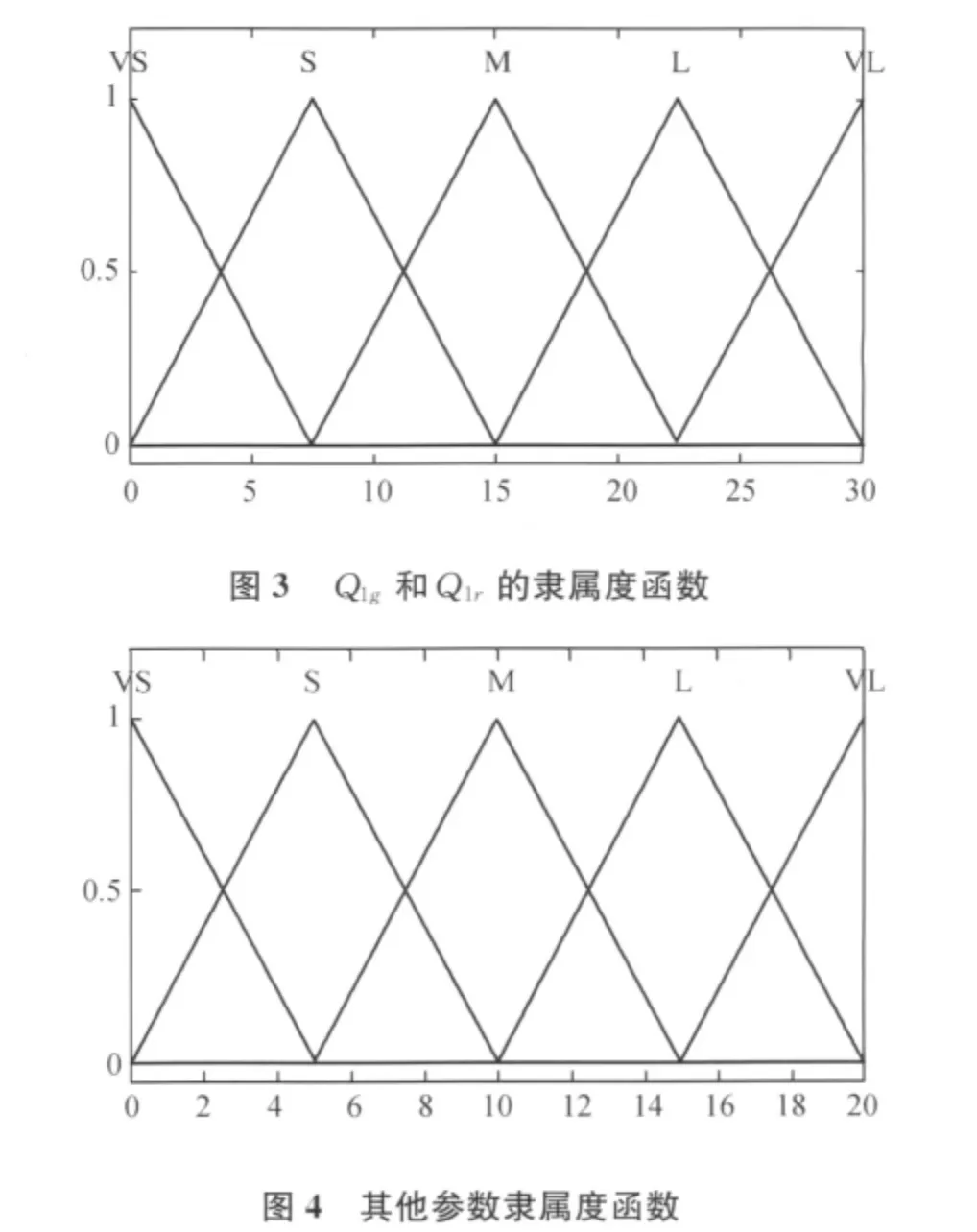
其中，Q1g和Q1r都是指车辆排队长度之意，而且范围为（0，30），故隶属度函数一样，如图3所示。

t1g，t1r，Q21，Q12通过比例因子调整使3者的范围落在（0，20）之间，U1g，U1r，GT1以及修正后的GT1范围也在（0，20）之间，因此，这几者的隶属度函数一样，如图4所示。

3.2 遗传算法对隶属度函数的优化

通过遗传算法对三级模糊控制器的所有输入输出参数的隶属度函数进行优化，得到最优解，使平均车辆延误更低。

对于三级模糊控制器，每个模糊控制器都是两输入、输出，共3个参数，每个参数都有VS（很少）、S（少）、M（中等）、L（多）、VL（很多）5个隶属度函数。VS隶属度函数中心顶点为0，VL隶属度函数中心顶点为范围最大值。本文主要是通过遗传算法对隶属度函数顶点进行合理分配，通过迭代计算以达到最小平均延误。

因此，本文只对 VS、S、M、L、VL 5个隶属度函数中的S、M、L 3个隶属度函数的顶点进行优化，并将平均车辆的延误倒数作为遗传算法的适应度。

遗传算法的具体运用步骤如下：

1）随机产生初始群体，群体数目为20个，每个群体的染色体（二进制码）包含了所有模糊控制器输入输出参数的S、M、L 3个隶属度函数顶点的二进制码，每个顶点占用5位二进制码；

2）适应度函数为车辆平均延误的倒数，适应度值越大，车辆平均延误越小。

3）选择算法，通过优胜劣汰的生物竞争规则留下适应度大的种群；

4）交叉算法，随机选取2个种子并对它们的染色体的某些二进制码进行交叉，产生新的种子；

5）变异算法，采用简单变异随机对每个种子染色体的某些二进制码进行变异，产生新的种子。

不断重复上述遗传操作，直至最大进化代数，得到最优解。

3.3 模糊控制规则的语言表达

1）绿灯相位排队长度Q1g与绿灯经过时间t1g的模糊控制器的模糊控制规则参见表1。

2）红灯相位排队长度Q1r与红灯等待时间t1r的模糊控制器的模糊控制规则参见表2。

3）绿灯相位繁忙度U1g与红灯相位紧迫度U1r的模糊控制器的相位切换值，模糊控制规则参见表3。

表1 绿灯相位繁忙度模糊控制规则

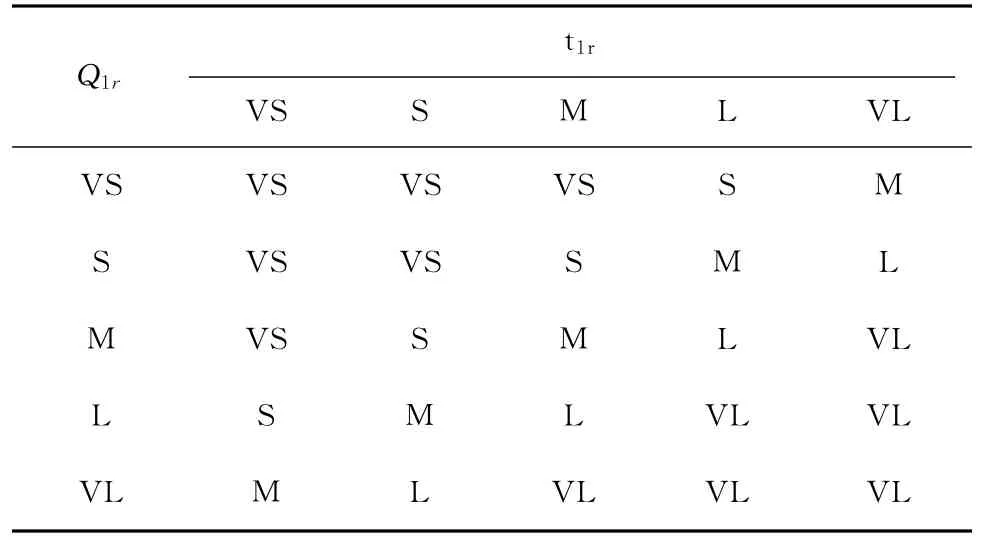
表2 红灯相位紧迫度模糊控制规则

表3 相位切换值模糊控制规则

4）相位切换值GT1与交叉口2驶向交叉口1车辆数Q21模糊控制器的协调相位切换值，模糊控制规则参见表4。

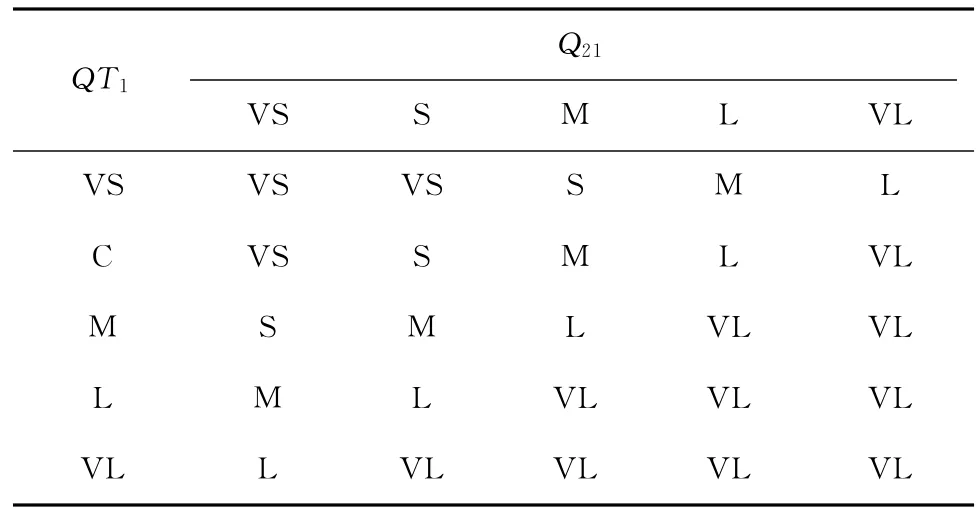
表4 协调相位切换值模糊控制规则

相位切换值GT1与交叉口1驶向交叉口2车辆数Q12的模糊控制器的协调相位切换值，模糊控制规则参见表5。

表5 协调相位切换值模糊控制规则

3.4 模糊推理及反模糊化

本论文采用MIN－MAX方法进行模糊推理规则计算，采用面积重心法进行反模糊化，从而得出清晰地结论。

4 对路口模型的仿真结果分析

4.1 评价指标

本文采用平均车辆延误作为评价指标，以评价该模糊控制算法的性能。

通过常理，可以知道，第i个交叉口第j个车道在第ts内产生的延误为

这里面，s（i，j，t）表示第ts末第i个交叉口第j个车道的剩余车辆数，s（i，j，t－1）表示第（t－1）s末第i个交叉口第j个车道剩余的车辆数，I（i，j，t）表示第ts内进入第i个交叉口第j个车道的车辆数，O（i，j，t）表示第ts内驶出第i个交叉口第j个车道的车辆数。

每秒内该车道剩余的车辆数就是该车道在这秒内产生的延误，因此，计算某车道在仿真时间内产生的总延误只需要累计该车道每秒内产生的延误即可。

4.2 仿真结果

笔者用MATLAB7.1编写了相邻双交叉口三级模糊协调控制的仿真程序，并进行仿真。

在仿真中，做如下假设：两感应线圈最大车辆数＝30；两交叉路口之间各方向运行最大车辆数Qmax＝100；当车辆到达率≤0.25辆／s时，车辆的到达服从泊松分布，当车辆的到达率＞0.25辆／s时，车辆的到达服从2项分布；由于干道与支道的车流量存在差距，此时假设支道车辆到达率为干道车辆到达率的0.8倍；各相位最小绿灯时间为15s，最大绿灯时间为60s；在每个到达率情况下的仿真约为1200s。

表6给出了不同到达率情况下相邻双交叉口三级协调模糊控制与单独交叉口模糊控制下产生平均车辆延误比较结果。从该表中我们可以看出，本文算法相对于传统孤立控制算法能够有效地减少经过交叉路口的所有车辆的平均车辆延误。

表7给出了通过遗传算法优化相邻双交叉口三级协调模糊控制算法后，得出的平均车辆延误与优化之前产生的平均车辆延误的比较结果。通过该表我们可以看出通过遗传算法对各级模糊控制器的输入输出参数的隶属度函数优化后，能够有效地减少平均车辆延误。

表6 两种方法不同到达率下仿真产生车辆平均延误结果

表7 遗传算法优化后的平均车辆延误与优化前比较

5 结束语

基于对专业知识的研究，本论文提出了一种相邻双交叉口的三级模糊协调控制算法，并且应用遗传算法进行优化的思想。依此设计了相应的三级模糊协调控制器，并利用MATLAB7.1编写了仿真程序，与传统的单交叉口模糊控制方法进行了比较。通过上一章呈现的仿真结果表明，本论文的三级模糊协调控制算法可以有效的减少平均车辆延误，并且产生的延误更加小于传统的单交叉口模糊控制方法所产生的延误。最后，通过遗传算法对三级模糊协调控制算法进行优化，并产生了显著的效果。作者下一步计划将研究连续相关联三交叉口的协调控制算法，并进一步将此方法推广到城市干道交通信号控制里去。

[1] 庞尚珍，徐金龙.智能交通系统中的车牌识别技术与研究[J].数字技术与应用，2010（9）：9.

[2] 李灵犀，高海军，王飞跃.两相邻路口交通信号的协调控制[J].自动化学报，2003，29（6）：947－952.

[3] 杨立才，贾磊，王红.双交叉口两级模糊协调控制算法的研究[J].系统工程理论与实践，2005，6（6）：33－38.

[4] 彭小红，刘国东.单交叉口多相位模糊控制及仿真研究[J].工业控制计算机，2004，17（12）：39－40，46.

[5] 李威武，王慧，钱积新.基于遗传算法的城域交叉路口两级模糊控制[J].中南工业大学学报，2003，34（4）：373－376.

[6] 刘智勇.智能交通控制理论及其应用[M].北京：科学出版社，2003.

[7] 高海军，李灵犀，陈龙.交通路口可变相位信号控制[J].交通运输工程学报，2003，3（3）：79－83.

[8] 高俊侠.城市单交叉口交通信号模糊控制系统的设计与仿真[D].北京：北京工业大学，2004.