PID控制器的模糊优化与参数学习自整定

谭显坤，宿靖波，李 雷

1．重庆交通大学国际学院，重庆 400074;2．重庆大学自动化学院，重庆 400044

1．Introduction

With speedy development of control theory and technology，although lots of excellent controllers have been appeared，but it has still taken over the leading position in industrial control system to the conventional or improved PID controller because of being correspondingly simple in its structure，convenient in application，clear in physics conception，and adjustable in hand work for control parameter．But the control parameter，which is the disposable tuning setting，is difficult to ensure to be in the best status of system running process all the time［1-4］．Once the system is suffered from external disturbance，and the system can be deviated from the expected state．Therefore it is the puzzle of controller design for how to select control parameter．In consideration of the fuzzification of selecting parameter in hand work tuning，it is needed to summarize up the control experience and make the control rule，and it must be repeatedly tried to obtain the proper control parameter．Therefore under the condition of a certain constraint，it is worth to research about the method for ensuring the index such as control amount，overshoot，system error and rise time etc in whole system performance．

2．Fuzzification of control parameter tuning

As a result of being different in contribution of system performance index for different control parameter of proportional gain KP，integral coefficient KI，and differentiate coefficient KD，it is not compatible among the index of system performance．For example，it is better in speedy response but it is not as pretty in smoothness，and it is strong in robustness but it is not necessarily high in control precision．There are many contradictions among dynamic and static index．The performance of PID control system is realized by the main index of speed response，overshoot，steady-state accuracy and stability etc，and the key factors affecting the index are determined by the selection and reasonable collocation of control parameter KP，KIand KD．The system’s contribution of KPis to accelerate the response speed of the system，and the larger KPis conducive to improve the control precision，but the excessive KPprobably leads to system instability．KImainly contributed to eliminate the control error of steady state，and KDis propitious to improve the dynamic characteristics of system，but their parameter values must be appropriate．The three control parameters of KP、KIand KDdirectly influence the output properties of the system，and therefore the manual adjusting method has its fuzzification．It can be solved through fuzzy optimization by learning based parameter auto-tuning method．

3．Tuning principle of control parameters

A negative feedback control system is shown in Fig．1．In which，r(t)，y(t)is respectively the input and output of system，e(t)=r(t)-y(t)shows the system error，and u(t)is the output of the controller．The point located in different regions is different in error and its rate of change，shown in Fig．2，and the characteristic model is also different．It not only reflects the process of qualitative decision selection according to the running state recognition and the corresponding control mode，but also it previews the control method for the specified control mode quantitatively．Fig．2 shows that principle of parameter tuning directly is related to|e|and|ec|［5-6］．

When the|e|changes，it can be divided into three situations．① When|e|is large，in order to improve the response speed KPis a larger value．At this time if|ec|is large then the KDvalue also should be taken larger，and if|ec|is smaller then the small value of KDshould be taken．In order to avoid overshoot and prevent integral saturation，generally the KIvalue is smaller．② When|e|is moderately medium，in order reduce the overshoot the KIshould take a smaller value，and KPand KDvalues can be moderate so as to avoid the response speed is too slow．③When|e|is smaller，the KPand KIvalues should be increased so as to ensure the steady state performance of the system．In order to improve the anti-jamming performance and void system oscillation near the set point，usually the smaller values of KDshould be taken．

Fig．1 Closed-loop control system

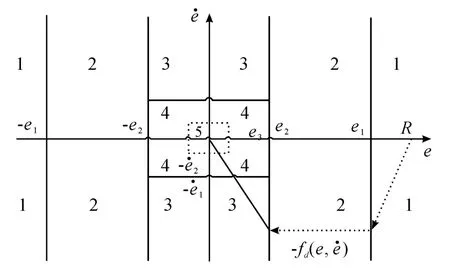
Fig．2 Control characteristic model

When the|ec|changes，there are three situations．① When|ec|is small，the larger KPand KIvalue can ensure fast response speed．In order to improve the anti jamming performance，if|e|is smaller then the KDvalue is smaller，and if|e|is larger then the KDvalue of medium size can be taken．② When|ec|is the medium size moderately，the KPand KIcan increase the response speed so as to take good steady state performance and the small and moderate values of KDcan avoid the system oscillation near the setting value and improve the anti-interference performance．③ When|ec|is larger，in order to prevent overshoot and ensure the system response speed and steady state performance，the value of KItakes small，the KPtakes the values as small as possible，and the KDvalue can take the larger．

Based on the above parameters tuning principle，it can determine the control parameters and adjustment rules by means of methods based on the combination of fuzzy optimization and PID control，and avoids manual adjustment based on experience and trial and error disadvantages repeatedly．

4．Auto-tuning of fuzzy PID parameters

4．1．Principle of parameter auto-tuning

The form of discrete PID control law is as the follow．

In which，KP，TI，TD，T，and k is respectively the proportionality coefficient，integration time con-stant，differentiating time constant，sampling cycle，and sampling serial number．e(k)，u(k)is respectively the deviation value at sampling time k and controller output value，and e(k-1)is the deviation value at sampling tim e(k-1)．Its incremental control algorithm is as follow．

In which，u(k)=u(k-1)+ Δu(k)，KI=KPT/TI，KD=KTD/T．

Based on the fuzzy reasoning，the fuzzy parameter auto-tuning PID controller can make online auto tuning for PID parameter KP、KIand KDin terms of the value at different time by means of the fuzzy control rules，and the structure of fuzzy PID control system with learning based parameters auto-tuning is shown in Fig．3．

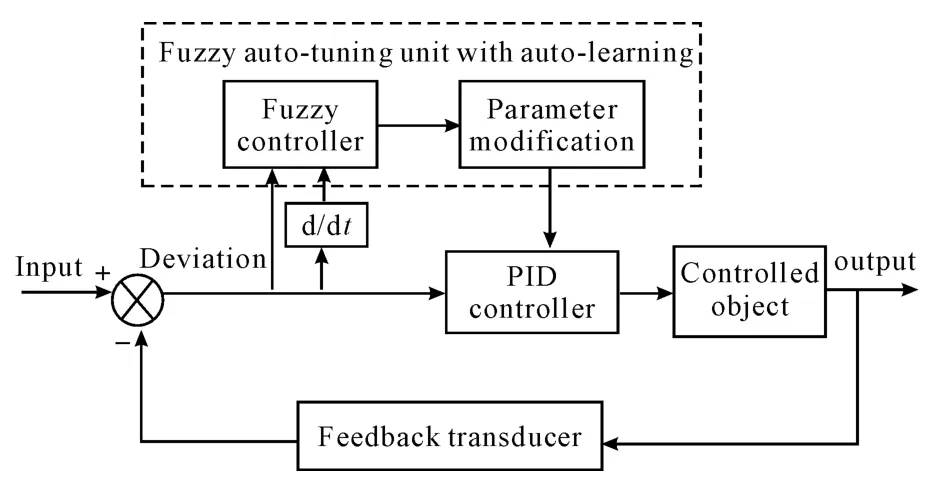
Fig．3 Structure of control system

4．2．Processing of control parameters fuzzification

In the Fig．4，the input is e(k)and ec(k)，and the output isΔKP，ΔKIand ΔKD．Owing to the input being the accurate number，therefore it must first make the fuzzy quantization，and determines the basic domain and domain of fuzzy set of variables as well as quantization factor Ke，Kcand Ku．The control parameter has more influence for dynamic and steady performance of fuzzy control system．It can be partitioned as seven pieces of fuzzy subset for the above input variable e(k)and ec(k)as well as output variable ΔKP、ΔKIand ΔKD．In which，NB，NM，NS，ZE，PS，PM，PB represents respectively the negative big，negative middle，negative small，zero，positive small positive middle，positive big．The all memberships of e(k)，ec(k)，ΔKP、ΔKIand ΔKDtake the symmetrical triangle function．According to the above，It can tune the fuzzy control rules table respectively aimed at KP、KIand KD．Now it takes KPas an example to make explain，and the fuzzy control rules table is shown in Tab．1，and ΔKI，ΔKDis similar to this．

Tab．1 Fuzzy control rule table forΔKP

Owning to all the membership functions being selected as symmetrical triangle function，and in the 49 pieces of fuzzy control rules，E and EC can respectively belong to two fuzzy subsets that the confidence level is not zero for the two adjacent subsets．For control rule:

If e is E and ec is EC thenΔKPis U．

The enabled fuzzy rule is only a maximum of 4 in a fuzzy inference process．

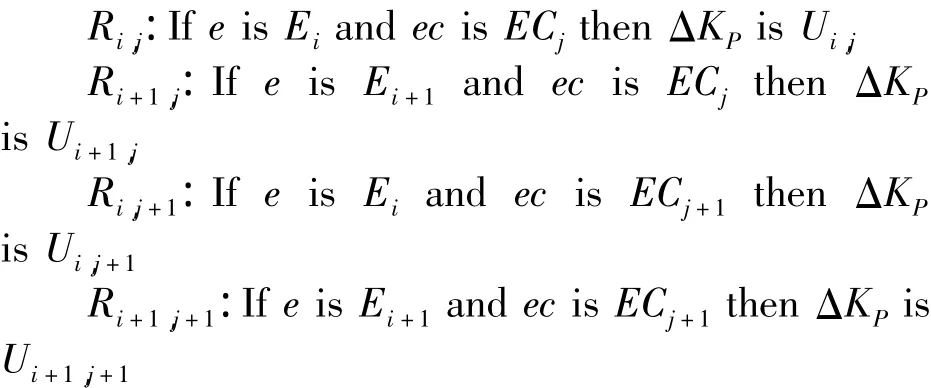
For any learning node of(e，ec，ΔKP、ΔKIand ΔKD)，all contain the related fuzzy information of the four pieces of control rule．

4．3．Fuzzy reasoning and defuzzification

For the fuzzy control rules，generally it uses the Mamdani reasoning method

Here the fuzzy implication takes small．

And the fuzzy synthesis takes big，namely the final conclusion U'is obtained from the synthetical reasoning U'1，U'2，…，and U'49．The inference rule is as follow．

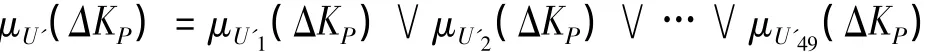
In a fuzzy reasoning at a certain sampling time，the value ofΔKPcan be determined by the barycenter of fuzzy output U'．Namely the rule，which the membership degree is zero，would not join the fuzzy reasoning．

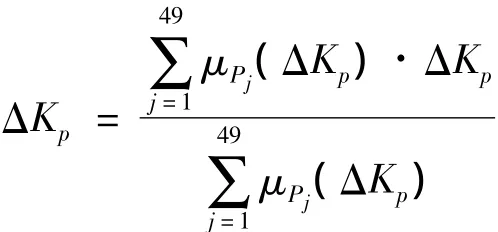
In which，μPj(ΔKP)(j=1，2，…，49)is the membership degree of ΔKP．In like manner，it can obtain the membership degree of ΔKIand ΔKD．Therefore it can obtain the controller parameter after being tuned．Assume the initial value is KP0，KI0and KD0，then it can the expression as follow．

4．4．Learning link design

The reference［7］proposed a sort of auto-learning based fuzzy control algorithm of MISO system．

Δy(k)=M［Δeu(k- τ -1)］

In which，Δy represents the output correction of fuzzy controller，Δy(k)is the output increment，Δeu(k)is the control increment，and τis the number of pure lag beat．It can calculate the correction Δeu(k-τ-1)of control quantity eu(k-τ-1)from incremental model．Because the control quantity and observed value of each step is stored into the storage，and it can take out eu(k-τ-1)from the storage．The control quantity should be revised as eu(k-τ-1)+Δeu(k-τ-1)，and then it is transformed into the fuzzy quantity Au．After that it takes out the measured value beforeτ+1 step，and transforms into the corresponding fuzzy quantity A1，A2，…，Ak，and from the above it can form a new rule．If there is the same first component rule in the rule base，then it is replaced with the new rule，and otherwise the new rule should be written into the rule base．Repeated the above process，until no rules need to be modified or appended．If the system has takenτbeat lag，then the response of the system contains all contributed results of the control beforeτ+1 beat．Because the algorithm makes the performance evaluation by means of current sampling value e and ec，the second component of control rule afterτ+1 beat must be updated by means of leaning algorithm based on Variable domain online reward and punishment．The aim is to improve the system lag characteristic．

1)Variable domain

After a period of time in work，it can find out the maximum and the minimum of e and ec in the period to be as the domain at the present stage．In view of the presence of external disturbances，if the rule of original small domain is difficult to make the state approach to the target，then it can enlarge the domain so as to meet the need．But the output domain still adopts the basic domain，and it can adjust the control output by means of reward and punishment factor．

2)Penalty function

Based on the system dynamic characteristic，it can summarize out that if e(k)·ec(k)＜0 then the system has the trend of increasing deviation，and if e(k)·ec(k)＞0 then the system has the trend of reducing deviation［8］．Therefore the evaluation function can be selected as c(k)=e(k)·ec(k)．If c(k)＞0 then it actualizes the reward for control rule，and if c(k)＜0 then it actualizes the punishment for control rule．In the ideal operation，it should ensure the deviation of online acquisition to tend to zero gradually，and therefore the penalty function is defined as the following．

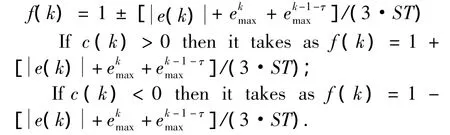
In which，τis the lag beat，ST is the maximum of system setting value，and ekmax、ekm-ax1-τis represents the maximum absolute value of the gained deviation of e at time k and(k-1- τ)respectively．

3)Algorithm flow

Step 1 Start self learning link．

Step 2 Read e(k)，ec(k)and e(k-1- τ)．

Step 3 Read u(k)，u(k-1- τ)，and rule number to be num(k)、num(k-1- τ)．

Step 4 Read the corresponding rule factor ω［num(k-1- τ)］of reward and punishment from data base in terms of num(k-1- τ)．

Step 5 Read ekmaxand ekm-ax1-τ．

Step 6 If ekmax≤0．1，then go to Step 8，or else go to Step 7．

Step 7 Compute c(k)，if c(k)=0，then go to Step 8;if c(k)＜0，then go to step 9;if c(k)＞0，then go to Step10．

Step 8 Penalty function f(k)=1，go to Step 11．

Step 9 Penalty function f(k)=1-［e(k)+ekmax+ekm-ax1-τ］/(3·ST)，go to Step 11．

Step 10 Penalty function f(k)=1+［e(k)+ekmax+ekm-ax1-τ］/(3·ST)，go to Step 11．

Step 11 Takeω［num(k-1-τ)］=ω［num(k-1-τ)］original value·f(k)，go to Step 12．

Step 12 End learning process．

5．Application of project

A tobacco production workshop has relatively strict requirement on the environment temperature．Generally it adopts the typical primary return air and constant air volume system to actualize the adjustment for ambient temperature．The desired temperature range is from 23℃ to 24℃，the time is not greater than 400 second when temperature is higher than 23．5℃ or lower than 23℃，and the rise time should be less than 150 second．It is difficult to meet the requirements of the production process technology by means of adjusting PID parameters manually．In the technological reform，it adopts the method of fuzzy optimization and learning approach with auto-tuning parameter，and based on the parameter auto-tuning of fuzzy PID controller，it realized a desired temperature control system．In the design process，it firstly transmits the actual temperature value in each workshop into the central monitoring system，then through computing it can obtain the control parameter of the next moment，and finally the control parameter is sent to the PID controller so as to make the temperature regulation．If the difference of the maximum difference among two deviation value is great or equal to 0．5℃，then the auto-learning link must be started so as to make the parameter online auto-tuning for current fuzzy control rule，otherwise，it does not enter the auto-learning link．The actual test and operation results show that the designed system can meet the requirements of the user technology process．

6．Conclusions

The engineering application practice shows that compared with PID control performance，the learning based parameter auto-tuning system of fuzzy PID controller has better adaptability．It is strong in robustness，high in steady-state control precision，and its superiority can better satisfy the high precision control condition．

［1］ XIA Deqian．Automatic Control Theory［M］．Beijing：Machinery Industry Press，2007．

［2］ LEE CC．Fuzzy logic in control systems［J］．Fuzzy logic controller systems：fuzzy logic controller-part1．EEE．Trans on SMC，1990(2)：404-435．

［3］ Sugeno M．An introductory survey of fuzzy control［J］．Information Science，1985(36)：59-83．

［4］ Astron K J，Hagglund．Automatic tuning of simple regulation［C］．Proceedings of 9 th IFAC World Congress．Budapest，1984，1867-1872．

［5］ LIAO Zhongfan．Fuzzy PID Parameter Self-tuning Technology and its Application in Central Air Conditioning System［J］．PLC ＆ FA，2006(10)：131-138．

［6］ HUANG Wei，WU Qian．Fuzzy-PID Controller of Parameter Based Auto-tuning and Its Application［J］．Hydromechatronics Engineering，2013，41(6)：81-86．

［7］ LI Shiyong．Fuzzy Control Neural Control and Intelligent Cybernetics［M］．Harbin：Harbin Institute of Technology press，2003．

［8］ LI Zushu，TU Yaqing．Human Simulated Intelligent Controller［M］．Beijing： National Defence Industry Press，2003．