强度折减法在抗滑桩加固土坡稳定分析中的应用

曹晓川 周 兵

(重庆交通大学建筑与土木学院，重庆 400074)

0 引言

土坡是具有倾斜坡面的土体。由于土坡表面倾斜，在本身重力及其他外力作用下，整个土体都有从高处向下滑动的趋势，若土体内部某一面(一般是曲面)上的滑动力超过土体抵抗滑动的能力，就会发生滑坡。边坡体的破坏属于破坏力学范畴，当滑面上每点都达到极限应力和极限应变状态时，材料进入破坏，此时岩土体抗剪强度得到充分发挥，这就是破坏力学中的破坏准则[1]。抗滑桩是近年来一种较为有效的边坡加固技术，加固土坡的抗滑桩，由于其被动地接受来自移动土体的压力，因而属于被动桩，与边坡土体共同构成复杂的受力体系。抗滑桩加固土坡的稳定性分析，特别是桩对土坡稳定的安全系数的影响，多年来已引起许多研究者的兴趣[2]。目前其分析方法可大致分为两类:基于土压力/位移分析的极限平衡法和有限单元/有限差分数值计算方法。工程实践中广泛采用极限平衡法进行抗滑桩加固边坡的稳定分析。但由于这类方法是建立在静力平衡基础上的，对于给定的滑动体系，需引入各种内力简化假定，消除超静定性而使问题近似地静定可解。根据极限分析概念，由此所得到的解答由于没有满足严格意义上静力许可内力场的基本条件，因此，这种极限平衡解既不是作为真实解的某个上限也不是真实解的某个下限。

与传统的极限平衡法相比，有限单元法能够全面满足静力条件、应变相容及应力—应变之间的本构关系，是一种理论体系更为严格的方法。另外因为是数值计算的方法，不受边坡几何形状的不规则和材料的不均匀之限制，因而是比较理想的土坡稳定分析方法[3]。

1 计算方法

Johnson证明了“若对理想塑性结构施以简单加载，则极限载荷与相同强度参数的刚塑性体的极限荷载相等”。一般的边坡，主要的计算控制量是岩体的剪切破坏，因而对塑性区的分布、大小计算精度要求较高，对位移的计算精度要求较低，因而本文中还是采用理想塑性模型。

1.1 强度折减法

建立在强度折减算法基础上的土坡稳定分析的基本原理是将土体的强度参数——粘聚力c、内摩擦角φ进行折减，得到新的强度参数 cf，φf，其表达式如下[4]:

其中，Ft为试算稳定系数;c为粘聚力;φ为土体内摩擦角;cf为折减后的粘聚力;φf为折减后的内摩擦角。折减示意图见图1。

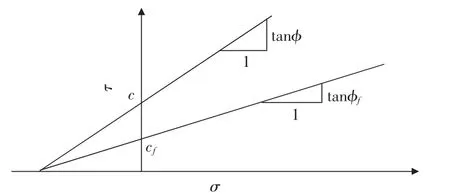
图1 土体强度折减示意图

1.2 计算步骤

先假定一个稳定系数Ft，若计算出的塑性区已经贯通，则说明假定的稳定系数过大，将稳定系数调小。逐步调整Ft的大小直到其增量足够小(可以接受即可)。在试算过程中可以采用二分法来进行，以加快收敛。

具体做法如下:

1)输入土体的粘聚力c、内摩擦角φ、压缩模量E、泊松比μ、重度等土工参数，此时的Ft=1。输入有限元程序计算。2)若上一步通过且塑性区尚未贯通，说明土体还未达到极限平衡状态，则假定较大的Ft(比如取1.5)，然后按照式(1)，式(2)来进行土体参数的折减，得到折减后的粘聚力cf，内摩擦角φf输入有限元计算。3)若通过则重复步骤2)，若塑性区已发展为贯通的塑性带，则取新的Ft等于最近一次塑性区还未贯穿的Ft与最后一次塑性区贯穿了的Ft的平均值，再依据式(1)，式(2)就算出土体的折减参数。4)一直重复步骤2)，步骤3)直到最后两次通过了的Ft之差的绝对值小于可以接受的值。这样就得到了土坡的稳定系数。

2 算例分析

某土质边坡采用抗滑桩加固，边坡高13.7 m，坡比为1∶1.73，在坡上设置单排抗滑桩，桩间距为2.5D(D为桩径)。土体参数为:重度 γ=19.63 kN/m3，粘聚力 c=23.94 kPa，内摩擦角 φ =10°，剪胀角 ψ =0，压缩模量 E=4 790 kPa，泊松比 v=0.35;抗滑桩为混凝土结构，采用线弹性模拟，参数为:重度γ=23 kN/m3，弹性模量为5×107kPa，泊松比 v=0.2，桩径 D=0.62 m，抗滑桩布置在距坡脚的水平距离为12.2 m的位置。

2.1 模型假设

假设钢筋混凝土均匀，边坡土体为均质各向同性体，符合Mohr-Coulomb模型:

1)因为抗滑桩为等间距布置，相邻两抗滑桩之间的土体在自重作用下可能在桩之间形成土拱效应。模型中取相邻两桩各一半及桩间土体为研究对象，见图2。2)将钢筋混凝土桩按均质材料分析，按受压区和受拉区分成两列单元，桩体与土体之间的接触，考虑为摩擦力与正压力成正比，而与桩土相对位移无关的模型。

2.2 单元划分与计算参数的确定

1)单元划分:模型共划分为1 352个，单元类型均采用C3D8R，其中桩单元80个，岩土单元1 272个，单元划分情况见图2。2)边界条件的确定:模型底部和前后边界条件根据文献[5]分别采用y方向和x方向约束处理，两个侧面则采用对称约束(以平面x—y为对称面)，其中y轴向上，x轴向后。3)计算参数的确定:计算过程中仅仅对土体材料的强度参数中的粘聚力c、内摩擦角φ进行折减，其他参数不变。

在抗滑桩和土体之间设置接触单元，桩、土之间的摩擦系数为 0.35。

Mises等效应力的表达式如下:

其中，S为偏应力张量。

按土体强度参数(此时Ft=1)计算得到的土体Mises等效应力云图如图3所示。

图2 有限元模型示意图

图3 土体Mises等效应力云图

等效塑性应变PEMAG的表达式如式(4)所示:

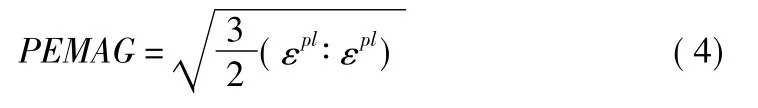
土体的等效塑性应变等值线图如图4所示。

从图4中可以看到，Ft=1时实际状态下土坡只有很小一部分处以塑性状态，此时土体对抗滑桩的作用力很小。但作为对抗滑桩的设计，不可采用实际的作用力作为设计荷载。因为土坡发生滑动是一个渐变的过程，在这个过程中荷载(重力)并未有多大的变化，而是土体本身的强度参数发生变化进而渐渐不能阻止坡体滑动。

由于Mohr-Coulomb模型中，材料的屈服与等效围压应力相关，随着等效围压的增大模型在π平面上的屈服面也呈线性的增大。对比图3，图4可以看到Mises应力等值的地方，相应的屈服状态却明显不同，这正是采用了Mohr-Coulomb模型的原因。

当取稳定系数Ft=1.5时，土体折减后的粘聚力c=15.96 kPa、内摩擦角φ=6.7°，按折减参数计算得到土体的Mises应力云图如图5所示。

图4 Ft=1时土体等效塑性应变PEMAG等值线图

图5 土体Mises应力云图

土体的等效塑性应变等值线图如图6所示。

从图6中可以看出当Ft=1.5时，抗滑桩以上边坡土体的塑性屈服面已基本贯通，而抗滑桩以下边坡土体的屈服面还未贯通，所以抗滑桩以上边坡先达到失稳破坏。

图6 Ft=1.5时土体等效塑性应变PEMAG等值线图

当Ft=1.5时，边坡内已经有部分土体发生塑性屈服，抗滑桩以下边坡的破坏从坡脚开始，逐渐向坡顶发展，其塑性区域为一弧状滑动带，与极限条分法中假定的圆弧滑动面具有较好的一致性。由于抗滑桩对上部土体的阻挡作用，抗滑桩以上边坡土体的塑性区则是先在桩附近出现，然后先沿竖向扩大一点再逐步向坡顶发展。当塑性区与顶部贯通时土坡也就产生了一个滑动面，若滑动面上的土体都达到破坏应力，土坡就会滑动。岩土体的破坏是一个渐变过程，破坏开始时整个滑面上都达到力的极限平衡状态，此时滑面上每点的岩土强度也都得到充分的发挥。随着滑面上塑性变形的增大，土体逐渐破坏，直至滑面上每点都达到塑性极限应变状态，滑面发生滑移破坏[1]。本算例中取稳定系数为1.5。

3 结语

抗滑桩已成为当今滑坡防治中的一种主要措施，被许多滑坡治理工程所应用，而抗滑桩与滑体之间的相互作用力非常复杂，通常抗滑桩稳定作用主要源自其对土体两方面的作用:1)桩的表面摩擦阻力将土体滑动面以上部分重力传递一部分至滑动面以下，从而减小坡体的滑动力;2)桩体本身刚度提供的抗滑力直接阻挡土体的滑动。本文利用数值模拟的方法对底端嵌固的抗滑桩的受力等情况进行了研究，得出以下结论:1)边坡治理设计多年来一直采用极限状态法，即传统方法中计算得到的岩土侧压力是在坡体滑移破坏且岩土体强度充分发挥时的岩土侧压力，按此设计，既能保证坡体安全，又能最大限度地节省经费。采用有限元强度折减法来进行支挡结构设计应遵循此原则。通常，当有支挡结构与岩土介质共同作用时，土体一般不处于极限平衡状态，而可能处于弹性平衡或者局部塑性极限平衡状态。这种受力状态不是设计情况下的受力状态，按此来计算支挡结构上的内力，会使设计偏于危险或偏于保守[1]。关于滑坡推力安全系数的定义，通常采用荷载增大的分项系数作为安全储备，这种方法通常在地面工程中采用，但这不适用于边(滑)坡受力状况，边(滑)坡工程中岩土体重量增大的情况不多，而且增大数值不大。常遇的情况是岩土体强度降低而导致坡体失稳，因而采用强度降低系数作安全系数更符合边(滑)坡实际情况[1]。2)采用有限元强度折减法，通过桩—土共同作用有限元模型计算得到了抗滑桩作用下边坡的稳定系数。与极限平衡法相比，强度折减法的优点有:a.滑动面的形状、位置无需事先假定。滑动面自然出现在土体材料强度不能抵抗剪应力的地方。b.由于是采用数值算法，可以模拟多种情况，而且也不需那么多的假定。保持了严密的理论体系。c.有限元解出的结果提供了应力、应变等全部信息，为设计提供了较为全面的依据。

[1] 郑颖人，赵尚毅.用有限元强度折减法求滑坡支挡结构的内力[J].岩石力学与工程学报，2004，23(20):3552-3558.

[2] 韩理安.水平承载桩的计算[M].长沙:中南大学出版社，2004.

[3] 陈祖煜.土质边坡稳定分析[M].北京:中国水利水电出版社，2003.

[4] Griffith，D.V.，Lane，P.A.Slope stability analysis by finite elements[J].Geotechnique，1999，49(3):387-403.

[5] GUIN J.Advanced soil-pile structure interaction and nonlinear behavior[D].New York:State University of NewYork at Bufalo，1997.