GPS 网基准兼容性的应变分析

白海明

(山西省地球物理化学勘察院，山西运城 044000)

GPS定位成果属于WGS－84地心坐标系，而现今实用的测量成果属于某一国家坐标系或地方独立坐标系(参心坐标系)，因此，实际工作中必须进行GPS网WGS－84坐标系成果至地面参心系的转换。对于平面转换，主要采用二维约束平差方法，即以地面网的已知点为约束条件，将GPS网强制附合到地面网中。我们知道，纯GPS网具有较高的相对精度，而以往用传统方法建立的地面网的相对精度却难以与GPS网相比拟。就我国而言，传统网存在分阶段建立和分区平差等弊端，再加上长期地壳的不均匀运动，使得地面点间往往难以兼容一致。当采用一组一致性差的点为基准，进行GPS网二维约束平差时，必然引起纯GPS网的扭曲变形，当这种变形不能容忍时，将极大地损坏GPS网的原有精度。因此，在进行GPS网二维约束平差时，进行基准点兼容性分析至关重要。分析GPS网基准兼容性的方法有多种，但大多对基准不兼容造成网的变形缺乏数量大小的概念和一定的几何解释。本文以基准点间的边长为对象，把弹性力学中的应变分析方法应用到GPS网基准兼容性的叛定，可以很好地解决以往存在的问题。

1 基本原理及方法

1)弹性力学中变形与应变的基本概念和有关关系式。由弹性力学理论可知，弹性体在外力作用下，物体的各点的位置要发生变化，即发生位移。位移实际上由三部分组成，它们是参考点的刚体平移、刚体的转动和纯应变。前两种位移后，仍保持各点间的初始状态的相对位置，而纯应变则改变了各点间的初始状态的相对位置，即产生了变形。这里我们主要研究后一问题。

在假定介质是连续均匀、各向同性和小形变的情况下，可方便地对弹性体进行应变分析。在二维状态下，弹性体内一点的纯应变，可用其应变参数 εx，εy，rxy描述，其几何意义为:εx，εy分别表示原来与X，Y轴平行的矢量单位长度的伸长(或压缩)，称为线应变，伸长为正，缩短为负;rxy为变形前与OX，OY轴正向一致的两正交线段在变形过程中发生的直角变化量，称为剪应变，直角减小时为正，反之为负。

εx，εy，rxy的大小与坐标轴有关，在众多的任意方向轴的应变中，存在着一对互相垂直的特殊方向，这对坐标方向存在最大和最小线应变ε1，ε2，其间的剪应变为0，称主应变，并有以下关系式:

其中，r为总剪切;λ为总应变。

任意方向a上的线应变εa与该线段平均应变状态分量之间的关系式如下［1］:

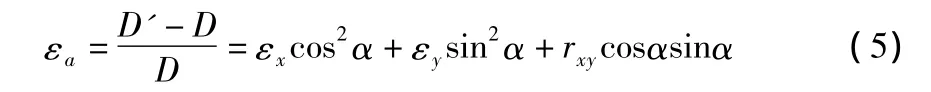
其中，D，D′分别为方向a上边长变形前、后的长度;α为该边方位角。

从式(5)可知，只要已知任意三个不同方向上的三个边长D，D′及其方位角α，就可组成三个线性方程，从中解出三个应变参数εx，εy，rxy(当多于三边时采用后述平差方法)。式(5)是本文进行应变分析采用的基本关系式。

2)利用已知点间边长进行GPS网基准兼容性的应变分析原理和方法。

如前所述，GPS网转换为地面坐标系时，常采用二维约束平差，实际上是将纯GPS网强制附合到地面网中。如果将GPS网看作一弹性体，则地面网中已知点间平面边长与GPS网中相应的平面边长的差距，正是GPS网二维基准转换时将引起的弹性变形量。因整个GPS网变形量的大小，归根结底是由基准点间的变形来引起和决定的，若基准点间的变形量超过一定的限度，则整个GPS网的变形当然也就不可能容忍，因而，通过对基准点间边长，根据式(5)求得的平均应变量也就能说明整个GPS网的变形状态。如果对此应变量的大小加以恰当的限制，则可对基准兼容性进行叛定，这就是本方法的基本原理。

GPS网变形量限制条件可依不降低GPS测量精度为前提，同时满足生产需要为基本准则。为此文献［2］提出判定GPS网基准兼容性的两个准则:

准则一:最大与最小线应变之差不应超过GPS基线测量精度的比例误差:

准则二:最大线应变和剪应变也不应超过GPS基线测量精度的比例误差:

准则一是对GPS网与地面网转换时，变形量的均匀性要求，如果超过此限值，则GPS网将会产生较大扭曲，而准则二则是变形量大小的限制。

GPS网基准兼容性的应变分析步骤如下:

a.先进行GPS网的三维无约束平差，经各项检验合格后，再选择与地面网相同的参考椭球元素和投影面，以及一致的中央子午线，并固定地面任意一已知点，进行GPS网二维自由网平差(或称最小约束平差)。这时在二维平面内，纯GPS网的尺度就与地面网保持一致，并且仍保持GPS网其原有的精度。

b.计算(或摘录)已知的地面点间的高斯平面边长D′和经二维自由网平差后，纯GPS网中相应点间的高斯平面边长D和方位角α。

c.采用不同的基准组合，以间接平差法，分别求解不同组合条件下的三个应变参数 εx，εy，rxy。

为实际应用方便，式(5)作如下变换:

上式中把D作为非随机量来进行处理。因一般纯GPS网中边长的精度是很高的，再加上D与D′相比具有现时性(不存在变形影响)，这种处理不会引起应变参数太大的偏差，而能使计算简化。

对于多条已知边可以Di′为观测值，列立如下误差方程:

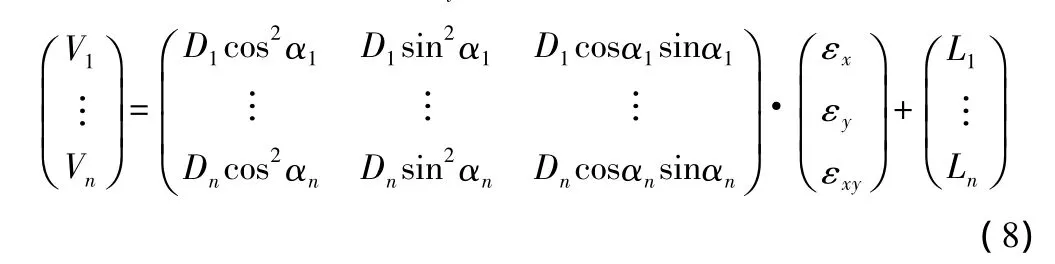
其中，Di以 km 为单位，Li=(Di－D′)/1 000(即 Li以 mm 为单位)。因D′的协因数阵往往不能直接给出，而一般情况下，边长中误差与边长成正比关系，为此，简便期间，D′的协因数阵可取如下对称阵:

Qdd也可根据相应等级边长相对精度分析给出。当已知边长度及精度相近时，也可直接采用单位阵E。

根据式(8)，式(9)即可按间接平差法求出参数 εx，εy，rxy，再据式(1)～式(4)算出其他参数。

d.根据求出的有关参数，以前述准则一、准则二为依据，分析判定基准点兼容性，从中选择兼容性好的已知点组，参与GPS网的二维平差，获得最终平差成果。

2 算例

如图1所示为一实测D级GPS控制网。

图1 D级GPS控制网

1，2，3，4为已知点，已通过各种方法判定其间一致性很好。为利用应变分析方法进行基准兼容性分析，现分别以两种情况给2号，4号点加入不同的误差进行分析对比。其中案例一给2号点坐标加入(3 cm，－3 cm)误差，给4号点加入(－3 cm，3 cm)误差;案例二给2号点加入(3 cm，－3 cm)误差，给4号点加入(－5 cm，5 cm)误差，分别计算其应变参数如表1～表3所示。

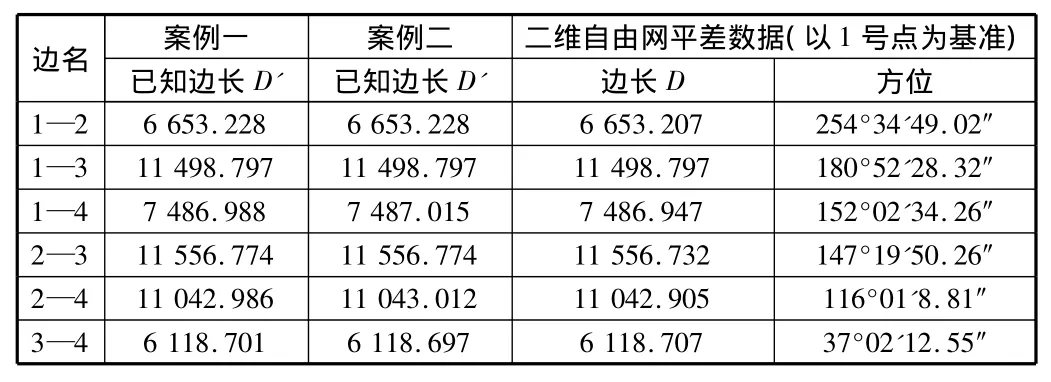
表1 计算用的基本数据表

表2 案例一不同基准组合下应变参数表

表3 案例二不同基准组合下应变参数表

因E级网的比例误差为b=10 ppm，根据准则一、二及上述表2，表3可知:

案例一情况下，1—4组合方案均满足要求，但以2方案为佳;而5组合方案总剪切较大，会使网产生较大扭曲，不可取。

案例二情况下，只有2方案满足要求，其他方案均不可取。从表3可分析认为，4号点与其他点间不兼容，这也与前述假定是一致的。

3 结语

本文利用基准点间边长进行GPS网基准兼容性的应变分析方法，既有数量概念，又有几何意义，能够对基准点不兼容而引起GPS网的变形有直观的判断和解释，并且具有较强的灵敏度。特别适用于具有多个已知点时的检验分析。由于通常已知点个数总是有限，而所求参数只有三个，因而，误差方程的组成和法方程的解算也就较为方便，不需要专用程序即可进行。上述算例的平差过程，就是笔者在Excel上实现的。通过实践证明，本方法具有一定的可靠性和实用价值。

［1］ 陶本藻.自由网平差与变形分析［M］.武汉:武汉测绘科技大学出版社，2001:170－183.

［2］ 张 勤，李家权.GPS测量原理及应用［M］.北京:科学出版社，2005:174－212.

［3］ 杨桂通.弹性力学［M］.北京:高等教育出版社，1998.