螺栓联接的预紧力与疲劳强度的讨论

郭卫凡 唐文良

（1.重庆工程职业技术学院，中国 重庆400037）

0 引言

轴向拉力作用下螺栓联接的失效多数为疲劳失效。统计表明百分之九十以上螺栓失效都与应力集中作用产生的疲劳失效有关。由于螺栓联接是一个多接触面的弹塑性接触问题，在重复加载作用下的应力应变关系十分复杂，并且影响疲劳强度的参素众多，因此，直接通过对螺纹的应力应变分析来计算螺栓联接的疲劳强度的实用意义不大。通常的做法是先计算出外力与预紧力作用下螺栓中的平均应力与变化应力，然后对应力集中，尺寸效应等影响疲劳强度的参数进行综合考虑，再应用古德曼法则来计算螺栓联接的疲劳强度。

一般情况下联接件的有效刚度远大于螺栓刚度。螺栓预紧力的存在，除了使零件之间产生紧密联接，增强联接的刚性之外，还会大幅度降低在拉伸载荷作用下螺杆应力的变化幅度，由此提高了螺栓联接的疲劳强度。 如果预紧力不够大，拉伸载荷有可能超过螺栓联接的预紧力，造成联接件分离，这会使螺栓联接的刚度大幅下降，同时也使应力变化幅度大幅增大而迅速降低螺栓联接的疲劳强度。增大螺栓联接的预紧力，不但能降低联接件在载荷作用下产生分离的风险，还能提高螺栓联接的防松能力， 防止预紧力在重复外力作用下变小。 以下分析从疲劳强度计算的角度来讨论螺栓联接预紧力对螺栓联接疲劳强度安全系数的影响。

1 螺栓联接疲劳强度安全系数计算

螺栓联接的疲劳强度可通过古德曼准则作近似计算。在周期循环应力作用下，根据古德曼准则，金属零件的持久极限疲劳强度曲线可由下式决定：

其中，Sa，Sm为古德曼持久极限疲劳强度线上任一点上对应的交变应力与平均应力，Su为材料的抗拉强度，Se为零件的综合疲劳极限强度。

零件的持久极限疲劳强度安全系数的计算与应力的加载路径有关。 对比例加载，零件持久极限疲劳强度设计的安全系数可用持久极限疲劳强度曲线上的应力幅度Sa与实际应力幅度σa的比值来定义[1]。

在外力作用为零时，螺栓联接中存在一个预紧力Fi作用。 预紧力在螺杆中产生的平均预应力可通过σi= Fi/ At计算， 其中Fi为螺栓联接的预紧力，At为螺杆的有效受力面积。 而在外力P 作用下，螺杆中对应的拉应力可由以下公式计算：

其中，kb为螺杆的有效拉伸刚度，km为联接件的有效压缩刚度。联接件有效压缩刚度可通过试验来确定，或通过对一个有效压缩圆锥体来进行简单有效的近似计算[1-2]。更精确的结果则可通过有限元分析来计算。

当一个螺栓联接受到一个循环外力作用时，如果外力作用P 与预紧力Fi都为已知， 则可求出在外力P 作用下螺栓中的交变应力幅度σa与平均应力σm。 螺栓内的交变应力幅值可由以下公式计算：

而平均应力则可通过公式（4）计算：

如果认为螺栓联接中螺杆的有效刚度与联接件的有效刚度在加载过程中都是常数，对一个给定的拉伸力作用，外力在σa-σm图上产生的变化为一直线变化关系。 螺栓联接的疲劳强度安全系数由nf= Sa/σa定义，可通过下公式来计算：

此时如果能确定对应螺杆的综合疲劳强度Se， 就可通过公式（5）求出在给定预紧力与外力作用下螺栓联接的疲劳极限强度及对应的疲劳极限强度安全系数。 在以上的计算中，没有考虑螺杆中的扭矩作用，这是因为在循环应力作用下，螺杆内的扭矩会很快被减低到对疲劳强度的影响可以忽略不计的程度。如果在整个循环加载过程中预紧力与零件综合疲劳强度Se都是常数， 则疲劳极限强度安全系数也是一个确定的常数。

由于螺纹在根部有很大的应力集中，在重复应力作用下螺纹根部疲劳断裂是螺栓联结疲劳失效的主要原因之一。在外力与预紧力作用下螺纹的受力呈不均匀分布，其中螺杆上受力螺纹的第一牙承受了最大份额的载荷。 因此，受力螺纹的第一牙根部的应力集中应是产生疲劳裂纹的主要原因之一。 由于螺栓及螺纹几何形状的标准化，螺栓联接疲劳计算的有效应力集中系数可通过分析或试验得出。螺栓综合疲劳极限强度可由以下简化公式确定：

其中S′e为螺栓材料标准试件的疲劳极限强度应力，kb为零件的尺寸效应系数，Kf则是一个包括了几何形状产生的应力集中作用及与材料强度相关的表面作用的疲劳强度降低系数，Kf与螺纹的设计形状有关，也与螺帽的几何形状有关。 实验表明，通过滚压加工产生的螺纹，其应力集中系数Kf小于通过切削加工产生的螺纹，有更高的疲劳强度[1]。

2 预紧力对螺栓联接疲劳强度的影响

如果拉伸外力小于预紧力，且无偏心作用，则交变应力不随预紧力变化而改变。 预紧力变大，交变应力不会改变，但平均应力会变大。因此，根据公式（5）计算得出的螺栓联接的疲劳强度安全系数就会变小。由此会得出增加预紧力可能会使螺栓联接的疲劳强度安全系数降低的结论。是否可以因此认为在不发生螺栓联接预紧接触面分离的前提下，螺栓联接的最大疲劳强度安全系数可通过一个最小的预紧力来实现呢？

对这个问题的回答，可从三个方面来讨论。首先，由于外载荷的不确定性，总是存在超载的可能，而超载后则可能使螺栓联接产生分离。需要考虑的是，增大预紧力所带来的疲劳强度的降低与可能的超载作用下产生螺栓联接分离后疲劳强度降低相比，那一个更具有更大的风险？ 其次，在循环外力作用下，预紧力可能逐渐降低，这对螺栓联接疲劳强度影响如何？ 再就是增大预紧力可能会在螺纹根部产生塑性变形，从而产生残余应力，这对螺栓联接疲劳强度有如何影响？

在拉伸外力作用下，联接件上的压力Fm可由下式求得：

联接件上的压力随外力增大而减少。由于联接件之间不能承受拉力，联接件产生分离的临界外力为：

利用螺栓联接的古德曼法则公式（5）来计算给定外力作用下螺栓联接的疲劳强度安全系数时，外力作用不能大于使螺栓联接产生联接分离的作用力Psep。在外力使螺栓联接产生分离的条件下，螺栓联接的疲劳强度可能会大幅降低。

如果外力使螺栓联接产生分离， 螺栓联接的疲劳强度安全系数nf1可以通过Ps/P 来定义， 其中P 是外力作用幅值，Ps是加载曲线σaσm与疲劳强度曲线Sa-Sm的交点对应的外力作用。 很容易证明，此时的疲劳强度安全系数nf1可通过下面公式来计算：

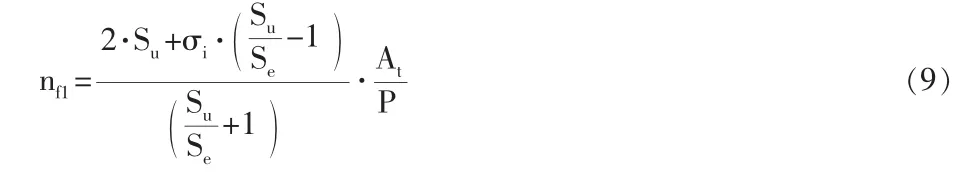
其中At为螺杆的有效受力面积。 以上公式可以证明，由于预紧力过低产生螺栓联接分离对疲劳强度的降低，远大于预紧力适度增加时对疲劳强度的影响。

根据公式（9），预紧力为零时，螺栓联接的持久极限疲劳强度安全系数为最小。 当外力作用使螺栓联接产生分离时，预紧力的增大能提高螺栓联接的疲劳强度。螺栓联接的疲劳强度安全系数随预紧力增加而变大。而如果外力作用下在整个疲劳加载过程中都不会使螺栓联接产生分离，由公式（5）得到的结果则是预紧力越大，螺栓联接的疲劳强度就变得越小。而且，如果预紧力可以很大，计算得到的螺栓联接疲劳强度可以变得非常小。

以上的分析似乎也表明，一个适当的预紧力对螺栓联接持久极限疲劳强度的最大化非常重要。但是，通过对下面两个因素的讨论，实际结论却是在正常条件下，预紧力越大，螺栓联接的有效疲劳强度也越大。

我们可以设计一个螺栓联接， 使得在任何可以预测的外力作用下，螺栓联接都不会产生分离，则螺栓联接的疲劳强度安全系数可以用公式（5）来计算。 但是，在周期载荷作用下，特别是在振动与脉动冲击力作用下螺栓联接可能产生振动松弛，这会使螺栓联接失去相当一部分预紧力。 由此会导致使螺栓联接产生分离的临界拉伸力变小，最后在外力作用下可能产生联接分离，使得螺栓联接抵抗疲劳失效的能力大幅降低。 这时螺栓联接的疲劳强度安全系数只能用公式（9）来计算。 而增大螺栓联接的预紧力，能大幅提高螺栓联接抵抗振动松弛的能力，从而提高了螺栓联接的抵抗疲劳失效的能力。 螺栓联接一旦产生分离，往往同时还伴有动态冲击力作用，使螺栓联接抵抗疲劳失效的能力进一步降低，增大了疲劳破坏的风险。

普通螺栓联接的螺杆拉力主要被最前面的三牙受力螺纹承受，当初始预紧力足够大时，会使部分螺纹根部局部进入塑性变形，同时在这些螺纹根部产生残余应力。 螺纹根部产生的残余压应力，能提高螺纹的疲劳强度。同时，塑性变形后的螺纹还能改善螺纹受力分布，使螺纹牙上的接触压力变小，由此也提高了螺纹的疲劳强度。如此的改变，还可能会使螺栓联接中强度最弱的部位被转移到那些强度相对更大的部位上去了。另外，在材料的屈服之后，螺栓联接的预紧力的进一步增加也会受到限制。因此，在不产生静力破坏失效的前提下，基本上是预紧力越大，螺栓联接的实际有效疲劳强度也越大。

如果螺栓联接的疲劳强度安全系数能满足预先的设计要求，此时应该是预紧力越大，螺栓联接抵抗联接分离的能力越大，抵抗预紧力松弛的能力越强，同时螺栓联接的实际有效疲劳强度也越大。因此，增大螺栓联接的预紧力，总体来说有利于提高螺栓联接抵抗循环外载作用下疲劳失效的能力，使螺栓联接在振动冲击力与有限超载作用下产生疲劳失效的风险变得更小。

3 结束语

在螺栓联接中产生与保持足够大的预紧力，是保证螺栓联接疲劳强度的重要手段之一。综合本文以上分析讨论结果，对钢制标准螺栓，在不超过螺栓联接的螺杆，螺纹与联接件的静强度的前提之下，对一个给定的螺栓联接设计，可以认为是预紧力越大，其有效疲劳强度也就越大。 如果不需要考虑撤卸后螺栓的重复使用，则在螺栓联接中产生的预紧力可以接近甚至达到螺杆的屈服应力。

［1］Joseph Edward Shigley, Charles R. Mischke.Mechanical Engineering Design[M].5th ed. McGraw-Hill, 1989.

［2］John H. Bickford. An Introduction to the Design and Behavior of Bolted Joints[M].2nd ed. Marcel Dekker, Inc., New York, 1990.

［3］西北工业大学机械原理及机械零件教研室,编,濮良贵,主编.机械设计[M].高等教育出版社,1989.

［4］浙江大学九院校,合编,刘鸿文,主编.材料力学[M].人民教育出版社,1979.