巨型城市区域的复杂网络特征*

赵渺希 朵朵

(华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640)

随着全球化进程的加速，城镇密集区域的空间组织 成 了 相 关 领 域 的 研 究 热 点［1］，Hall、Taylor等［2-3］对巨型城市区域的空间网络进行了实证研究.在现实世界中，各类地域“流”表征了城市体系中多样化的功能关系.由于针对巨型城市区域的研究在方法论上从属于世界城市网络的研究，因此在研究对象方面或集中于生产性服务业网络、或聚焦于城市区域内部的通勤联系，没有对城市网络中不同产业类型的链接进行比较，也没有相对完整地测度城市联系的复杂性［4-6］.近年来，研究对象、研究方法的日益丰富为不同类型网络之间进行横向比较提供了可能性［7-8］.

另一方面，作为图论衍生出来的分析工具，复杂网络具备了相对完整的统计量，并在物理学、生物学、社会学等交叉学科领域引起了广泛的重视，一些国际权威杂志相继刊发了相关成果［9-10］;近10 余年来，更是在学术界掀起了复杂网络的研究高潮，点度分布、匹配性、邻近性、中间性等组成了体系完整的统计量［11-12］.几乎在同时，Taylor 等［13-14］基于多区位公司的网络视角，对世界城市、全球城市作出了开创性的研究;Alderson 等［15］则对全球主要跨国公司的总部链接进行了研究;由此世界城市网络的研究也成为了研究热点.目前，西方学术界更加注重对世界城市网络的方法论探索，部分学者开始以多学科的视野来研究城市网络链接［16-19］.

有鉴于此，依据“企业是城市的作用者”这一观点，文中以复杂网络的统计量实现对巨型城市区域内不同产业类型的网络分析，试图弥补城市网络研究领域中既有分析工具的不足.

1 基础数据

研究在Alderson 等［15］的思路的基础上，以珠三角区域2009 年企事业单位名录为基础，并将样本对象扩展到了所有具有母-子关系的多区位企业，通过企业分公司的母公司来源地和分公司的注册地信息，形成企业总部-分支机构的权重型关系数据.研究的产业类型包括制造业、建筑与勘察、生产性服务业、商业贸易、交通运输与仓储、技术与公用服务、政府管理、企业管理8 大类.

2 珠三角区域的城市联系

为分析不同产业类型城市间联系的复杂网络特征，定义Tij，e为e类产业中i、j 城市之间总部在i 城市、且到j 城市设立分支机构的总部-分支型链接值，以此来分析不同产业类型城市间网络的特征.不考虑方向性，在总共m 个产业类型中，将城市i、j 之间的全部联系定义为

同样，还可以进一步对全部产业类型进行加和，即定义总部在i 城市、且到j 城市设立分支机构的方向性链接值为Tij.依此，通过对文中所用基础数据中总部-分支机构的联系进行Tij值分析可以发现，珠三角区域最大的联系为深圳 广州的企业分布，即总部位于深圳、分支机构位于广州的企业最多，其企业数量达到了1071 家，且该值远远高于总部位于广州、分支机构位于深圳的企业数量(599 家).珠三角区域各城市间的Tij值如表1 所示.从Tij值来看，广州-深圳两大核心城市之间的联系最为紧密;深圳 东莞、广州 佛山、广州 东莞、深圳 佛山的联系也均在200 家企业以上.总体上，深、莞、广、佛4 个城市内部的经济联系十分频密，而其余城市之间的联系则相对较弱.

表1 珠三角区域各城市间的Tij值Table 1 Tij values of different cities in the Pearl River Delta

不考虑方向性，由图1 所示的8 大产业类型的城市间的联系可见:建筑与勘察、交通运输与仓储、制造业、商业贸易4 大产业类型的城市间联系相对频密，且制造业、商业贸易中深圳和广州之间的联系比重远高于其他城市之间的比重;建筑与勘察、交通运输与仓储的高权重联系空间分布相对分散;其次，政府管理、技术与公用服务的联系在区域中分布相对稀疏，政府管理的联系分布最为稀疏;生产性服务业体现出广州、深圳之间的强联系特征，其余联系也多以这两个城市为中心往外辐射.

3 点度分布特征

3.1 点度分布的统计量

在城市体系的研究中，规模分布是常用的分析方法.巨型城市区域的一个重要特征即在于体系中节点规模分布的相对均衡性［20-22］，Hall 等［2］也曾用位序-规模曲线来描述多中心城市区域的特征.一般地，在不考虑链接权重的情况下，根据Tij对边值aij先行赋值(Tij大于0 则将aij记为1，Tij等于0 则aij亦为0)，由此，在无权网络中节点城市i 的点度ki即为其邻接矩阵N 的联系总和，根据Boccaletti 等［23］的研究即得下述公式:

式(2)只能针对无权网络进行度量，在权重型的复杂网络中，则须进一步定义wij为城市i 至j 的联系权重，并将每类网络中最大的链接值归一化为1，wij是任意两个城市i 和j 的链接值相对于最大链接值的比值，其取值分布在0～1 之间.这一定义可以顺推至各个产业类型的联系权重.

对于复杂网络的点度分析，同样借鉴Boccaletti等［23］的研究，并结合出度、入度进一步定义权重型网络节点入度()、出度()、总点度(si)的公式分别为

点度的分布可借鉴Newman 对复杂网络的研究，计px'为点度等于x'时节点城市的分布概率，Px为点度大于x的累积分布概率，根据Newman、Boccaletti、

陈彦光等的研究［11，23-25］，在实际的地理空间可以观察到累积分布概率Px的幂律分布特征，其中Newman 关于累积分布概率的分布模型可表示为

图1 珠三角区域不同类型产业的城市网络Fig.1 City networks of different industries in the Pearl River Delta

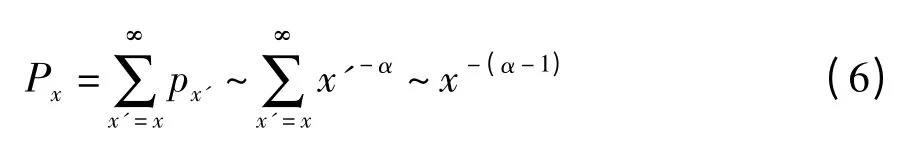
式中，x、x'是总点度si的阈值，α 为回归方程的参数.在城市地理研究领域，通过数学变换，可将x 视为位序，则上述公式成为位序模型的另一种表达形式.

对于权重网络中综合点度的均衡性，根据何大韧等［26］的研究可以通过信息熵(H)予以度量，该值越大意味着节点规模的无序性越大，按照前述定义，通过总点度si可以计算信息熵:

3.2 珠三角的点度分布特征

对每一产业类型的城市网络计算出度sout、入度sin之和即点度s，在此基础上进行排序计算节点城市的累积分布概率Px.珠三角区域城市累积分布概率的幂律分布特征如表2 所示.由表2 可见，8 大产业类型的城市网络的累积分布概率Px随着x 的增长呈幂律形式上升，且回归方程的决定系数都大于0.7.累积分布概率的幂律分布特征体现了珠三角区域的空间极化特征.

运用信息熵对各产业类型网络的均衡性进行分析，珠三角区域各产业类型的信息熵如表3 所示.由表3可知，8大产业类型中建筑与勘察、生产性服务业、交通运输与仓储的信息熵最为突出，说明这些产业类型的点度分布相对无序，而技术与公用服务、商业贸易的点度分布则相对较为有序.明显地，以满足所在地需求为主的政府管理、企业管理组织在网络中区域差异较小，而建筑业、生产性服务业、交通等类型的企业分支机构则具有更突出的地理集聚特征.

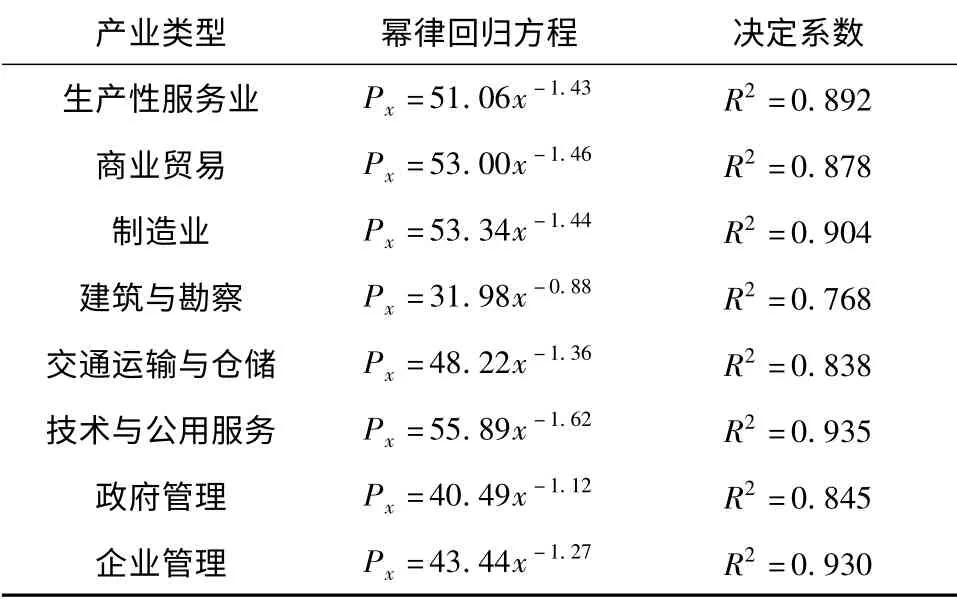
表2 珠三角区域城市累积分布概率的幂律分布特征Table 2 Power law characteristic of accumulated distribution probability for cities in the Pearl River Delta

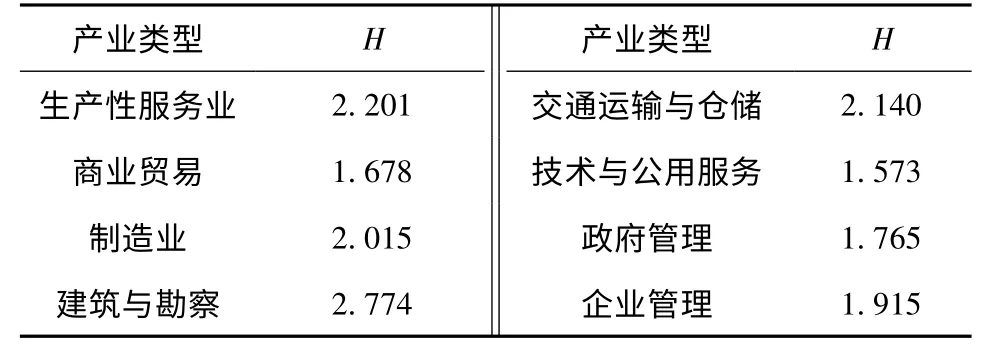
表3 珠三角区域各产业类型的信息熵Table 3 Information entropy of different industries in the Pearl River Delta

4 链接方向特征

4.1 链接方向的统计量

在以企业为分析对象的城市网络研究中，出、入度往往被忽视，这也与既有数据自身特征有关.Alderson等［15］的研究则关注了总部的控制能力，总部和分支机构的控制、被控制地位从一个侧面反映了城市间“流”的方向性;Burger 等［27］提出了多中心城市区域的多向性链接特征，Limtanakool 等［7］则对方向性问题进行了深入的探讨，并提出通过节点的出、入度差值来观察对称性，其相对于总点度的比值能反映节点i 出、入度的对称程度.

式中，NSIi取值在-1～1 之间，当NSIi=0 时节点的出、入度相等，而NSIi=-1 时为净流出，NSIi=1 时为净流入.进一步地，式(8)还可以顺推至各大类型产业的城市网络分析.

4.2 珠三角区域的链接方向特征

珠三角区域各城市的不同产业类型的出、入度如表4 所示，以出度来衡量珠三角区域总部机构的分布.由表4 可见，在8 大类型的总部区位的前两位城市中(表4 中粗字体)，除政府管理以外，其余7 大类型均是广州和深圳拥有绝对的优势地位，体现了核心城市在珠三角区域中的控制能力.

表4 珠三角区域各城市不同产业类型的出度和入度Table 4 Out-degree and in-degree of different industries of cities in the Pearl River Delta

分支机构数量反映了一个城市在相应产业中的市场吸引力.观察表4 发现，广州有6 项入度值排在各产业类型的首位，另一个区域核心城市深圳仅在生产性服务业方面具有吸引力(入度略高于广州).若将各产业类型入度的前两位均纳入考虑，即在表4 中考察每一列中最大的2 个sin值，可以看出，除了广州和深圳外，东莞在建筑与勘察、交通运输与仓储，佛山在企业管理，惠州在建筑与勘察等产业类型方面具有区域吸引力.

珠三角区域各城市的总出度、总入度的非对称性如表5 所示.由表5 可见，仅有深圳、珠海、广州具有相对明显的出度(NSI ＞0)，其中深圳处于绝对领先的地位，反映了深圳在区域经济空间结构中的外向型特征;其余城市均是入度大于出度(NSI ＜0)，而东莞、中山两市NSI 值最低，反映了两地接受外地企业设立分支机构的吸引程度较高.

表5 珠三角区域各城市总出度和总入度的非对称性Table 5 Asymmetry of sum out-degree and in-degree of different cities in the Pearl River Delta

值得指出的是，Dicken［28］对跨国公司生产网络的不均等性进行研究后认为，在不同公司控制的生产系统各部分之间，有控制与被控制之别;Massey［29］也提出了“所有权关系决定社会关系”的观点，认为空间上的所有权关系变成了权力关系地理.从珠三角网络中总部(出度)、分支机构(入度)的分布可以判断，处于NSI 值两极的深圳、东莞表征了区域经济空间联系的非对称性特征，也是价值链在巨型城市区域内部的一种地理映射.

5 节点匹配特征

5.1 匹配性的统计量

在Friedmann［30］、Sassen［31］的研究中，虽没有刻意强调城市规模在世界体系中的重要性，但可以明显地看到，具有全球控制力的核心城市既构成了全球网络链接的主体，也是各自地域范围内的重要城市.但也有学者认为城市功能的作用并非完全取决于城市规模，基于横向联系的网络互补性是城市集合效应最大化的重要途径［32］，中小规模的城市在全球网络中也有可能承担着传统意义上大城市才有的功能［33］.进一步地，对于网络中的任何一个节点，点度较高的节点城市其点度规模既可能源自于较小节点间联系的流量累积，也有可能依靠与其他较大节点之间的高流量联系形成核心-边缘式的网络垄断，当然也有可能二者兼而有之.因此，分析网络链接的规模指向对揭示城市间的功能关系有重要的理论意义.

对于网络中的任何一个节点，根据邻居的点度规模可以分为:与较大规模节点之间的链接、与较小规模节点之间的链接，这称为复杂网络匹配性问题.应用方面，目前可查的文献主要是Wang 等［34］对航空网络的匹配性分析.一般地，可以根据Boccaletti 等［23］的匹配性公式分析无权网络中每个节点的平均邻接度(knn，i):

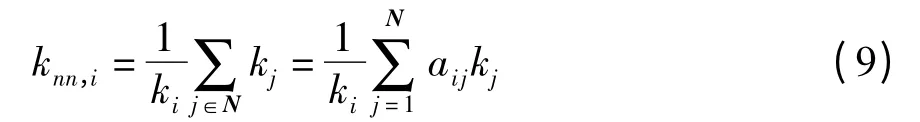
其中，N 是i 的邻接矩阵，而权重网络中节点城市的平均邻接度可以定义为［35］

式中，当si为0 时定义权重网络中的平均邻接度为0.通过无权网络的平均邻接度knn，i与权重网络的平均邻接度的大小比较，可以判别节点城市i 联系其他城市时对节点规模的链接趋向性.＞knn，i，表明i 的高权重边趋向于点度规模较大的节点，反之则意味着i 的高权重边趋向于点度较小的节点.对于无权网络、权重网络，整个网络的匹配性可以根据Leung 等［36］的研究，对任意一条连边的两端节点分别进行点度计算，并定义:

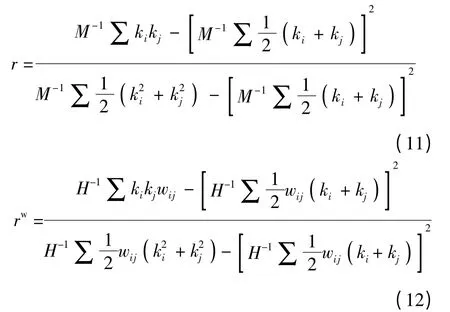
式中，r 为无权网络的全局匹配系数，rw为权重网络的全局匹配系数，M 为网络中连边的总条数，H 为网络中连边的总权重.

重新定义wij为节点i、j 之间无方向性的连边权重;r 取值在-1～1 之间，r ＞0 意味着该网络为同向匹配网络，r ＜0 则为异向匹配网络.在此基础上比较r、rw的大小可以判断高权重连边两端节点的规模相似性，rw＞r 意味着链接主要存在于点度规模相似的节点之间;rw＜r 则为异向匹配网络，意味着链接主要存在于点度规模差异较大的节点之间.

5.2 珠三角区域的匹配性特征

珠三角各个城市的平均邻接度如表6 所示，在无权平均邻接度(k)、权重平均邻接度(kw)两项数值中，广州、深圳得分相对于其他城市较低，实际上是这两个规模最大的城市其节点邻居的点度较低的结果，而中山的两项低值数据则反映了该城市在整个网络中的边缘特征.比较平均邻接度的差值Δk，可以发现该值与城市规模有着较强的关联，显示出珠三角区域网络在一定程度上体现出规模依附特征，其中广州、深圳、珠海、佛山最为明显.

表6 珠三角区域各城市的平均邻接度的差值Table 6 Dvalue of average nearest neighbors degree of different cities in the Pearl River Delta

珠三角区域网络的全局性权重匹配系数如表7所示，通过分析无权匹配系数r、匹配系数差值(Δr)两项数据即可分析全局网络联系的规模指向.从r的计算结果来看，8 大类型产业的无权匹配系数均小于0，说明整体上珠三角区域网络结构仍呈现出一定的向心型网络特征，其中技术与公用服务的异配特征最为明显(r 值为-0.648);而商业贸易的无权匹配系数相对较高，这类产业的无权网络相对接近正则网络.比较各类产业的匹配系数差值，除了交通运输与仓储以外，其他各项产业均大于0，说明高权重联系发生于点度规模相似的城市之间，其中技术与公用服务、生产性服务业等高附加值产业类型的匹配系数差值最为突出，意味着这两类产业总点度较高的城市间(主要是广州、深圳)的链接非常突出，反映了广州、深圳之间互相设立办事处、从事高端商务活动的空间格局，这也是对既有的生产性服务业城市网络研究的一个重要补充［37］.

表7 珠三角区域网络不同产业的匹配系数Table 7 Assortativity of different industries in the Pearl River Delta Network

6 结语

城市网络研究作为近10 余年来新兴的交叉学科，在经历过了广泛的实证研究以后，当前正处于分析方法和分析工具的讨论阶段，本研究即是基于这一发展趋势的响应.文中以珠三角区域为研究对象，重点通过链接方向、规模匹配等复杂网络的统计量梳理，试图揭示巨型城市区域内部价值区段空间组合的复杂网络表征.由于复杂网络涉及到的统计量十分庞杂，并且这一体系性的分析工具也还处于发展之中，因此文中对巨型城市区域的复杂网络研究仅仅只是阶段性的探索，对区域经济的空间网络全貌还有待深入探讨.

另一方面，并非所有复杂网络统计量都适合城市网络分析，尤其是对于当前西方流行的生产性服务业城市网络，更须辨清内在机理.根据Neal［16］、Liu 等［17］的观点，Taylor 关于世界城市网络研究的生产性服务业数据库是一种city-by-firm 形式的二模网络，若要将其映射为城市-城市的关系，则必须将其转置为一模网络，Taylor 的连锁模型虽然实现了二模网络向一模网络的转换，但是导致了城市间大量的无效联系，且采用乘法得到的一模网络尚存在学术争议，不可避免地对原有数据库造成了信息损失.进一步地，对于企业分支机构形成的城市网络，还须注意企业链接与城市链接的社会网络关系［38］，因此，一些常用的统计量如邻近性、中间性、群集性的应用都应从社会网络的角度予以慎重对待.

［1］Scott A，Storper M.Regions，globalization，development［J］.Regional Studies，2003，37(6/7):579-593.

［2］Hall P，Pain K.The polycentric metropolis:learning from mega-city regions in Europe ［M］.London:Earthscan，2006.

［3］Taylor P，Evans D，Pain K.Application of the interlocking network model to mega-city-regions:measuring polycentric city within and beyond city-regions ［J］.Regional Studies，2008，42(8):1079-1093.

［4］Taylor P，Derudder B，Witlox F.Comparing airline passenger destinations with global service connectivities:a worldwide empirical study of 214 cities［J］.Urban Geography，2007，28(3):232-248.

［5］Liu X，Neal Z，Derudder B.City networks in the United States:a comparison of four models［J］.Environment and Planning A，2012，44(2):255-256.

［6］赵渺希，陈晨.中国城市体系中航空网络与生产性服务业网络的比较［J］.城市规划学刊，2011(2):35-44.Zhao Miao-xi，Chen Chen.A comparison between airline passenger network and advanced producer service network in the urban system of China［J］.Urban Planning Forum，2011(2):35-44.

［7］Limtanakool N，Schwanen T，Dijst M.Developments in the Dutch urban systems on the basis of flows［J］.Regional Studies，2009，43(2):179-196.

［8］Burger M J，Van der Knaap B，Wall R S，Polycentricity and the multiplexity of urban networks［EB/OL］.(2013-02-14)［2013-05-22］.http:∥www.lboro.ac.uk/gawc/rb/rb420.html.

［9］Watts D，Strogatz S.Collective dynamics of‘small-world’networks［J］.Nature，1998，393(6684):440-442.

［10］Barab si A，Albert R.Emergence of scaling in random networks［J］.Science，1999，286(5439):509-512.

［11］Newman M.The structure and function of complex networks［J］.Siam Rev，2003，45(2):167-256.

［12］Newman M.Assortative mixing in networks［J］.Physica Preview Letters，2002，89(20):1-4.

［13］Beaverstock J，Smith R，Taylor P.A roster of world cities［J］.Cities，1999，16(6):445-458.

［14］Taylor P.Specification of the world city network ［J］.Geographical Analysis，2001，33(2):181-194.

［15］Alderson A，Beckfield J.Power and position in the world city system ［J］.American Journal of Sociology，2004，109(4):811-851.

［16］Neal Z.Structural determinismin the interlocking world city network［J］.Geographical Analysis，2012，44(2):162-170.

［17］Liu X，Derudder B.Two-mode networks and the interlocking world city network model:a reply to Neal［J］.Geographical Analysis，2012，44(2):171-173.

［18］Derudder B，Hennemann S.An alternative approach to the calculation and analysis of connectivity in the world city network［EB/OL］.(2013-02-14)［2013-05-22］.http:∥www.lboro.ac.uk/gawc/rb/rb401.html.

［19］Liu X，Derudder B.Analyzing urban networks through the lens of corporate networks:a critical review［J］.Cities，2013，31(4):430-437.

［20］Kloosterman R，Lambregts B.Clustering of economic activities in polycentric urban regions:the case of the Randstad［J］.Urban Studies，2001，38(4):717-732.

［21］Parr J.The polycentric urban region:a closer inspection［J］.Regional Studies，2004，38(3):231-240.

［22］Meijers E，Burger M J.Spatial structure and productivity in US metropolitan areas［J］.Environment and PlanningA，2010，42(6):1383-1402.

［23］Boccaletti S，Latora V，Moreno Y，et al.Complex networks:structure and dynamics ［J］.Physics Reports，2006，424(4/5):175-308.

［24］Clauset A，Moore C，Newman M.Hierarchical structure and the prediction of missing links in networks［J］.Nature，2008，453(7191):98-101.

［25］陈彦光，周一星.基于三角点阵模型的自组织城市网络探讨［J］.北京大学学报:自然科学版，2005，41(2):258-264.Chen Yan-guang，Zhou Yi-xing.Modeling self-organized network of cities based on the urban triangular lattice model ［J］.Acta Scientiarum Naturalium Universitatis Pekinensis，2005，41(2):258-264.

［26］何大韧，刘宗华，汪秉宏.复杂系统与复杂网络［M］.北京:高等教育出版社，2009.

［27］Burger M，Meijers E.Form follows function?Linking morphological and functional polycentricity ［J］.Urban Studies，2012，49(5):1127-1149.

［28］Dicken P.Global Shift:mapping the changing contours of the world economy ［M］.London:Sage Publications，2007.

［29］Massey D B.Spatial divisions of labor:social structures and the geography of production［M］.New York:Routledge，1995.

［30］Friedmann J.The world city hypothesis ［J］.Development and Change，1986，17(1):69-83.

［31］Sassen S.Global city:New York，London，Tokyo［M］.New Jersey:Princeton University Press，2001.

［32］Meijers E.Synergy in polycentric urban regions:complementarity，organizing capacity and critical mass ［M］.Amsterdam:IOS Press，2007.

［33］Neal Z P.From central places to network bases:a transition in the U S urban hierarchy，1900—2000［J］.City ＆Community，2011，10(1):49-74.

［34］Wang Jiaoe，Mo Huihui.Exploring the network structure and nodal centrality of China’s air transport network:a complex network approach［J］.Journal of Transport Geography，2011，19(4):712-721.

［35］Barrat A，Barthélemy M，Vespignani A.Weighted evolving networks:coupling topology and weight dynamics［J］.Physical Review Letters，2004，92(22):228701/1-4.

［36］Leung C C，Chau H F.Weighted assortative and disassortative networks model［J］.Physica A，2007，378(2):591-602.

［37］赵渺希，刘铮.基于生产性服务业的中国网络研究［J］.城市规划，2012(9):23-28，38.Zhao Miao-xi，Liu Zheng.Research on China’s city network based on production service industry ［J］.City Planning Review，2012(9):23-28，38.

［38］Rozenblat C.Opening the black box of agglomeration economies for measuring cities’competitiveness through international firms networks［J］.Urban Studies，2010，47(13):2841-2865.