一种基于欧氏距离的双目视觉三维重建算法

张鹏炜，蒋晓瑜，吕家国，裴 闯

(1.66393部队博士后科研工作站，河北保定071000;2.装甲兵工程学院，北京100072)

1 引言

双目立体视觉三维重建计算是对立体匹配结果进行量化处理的过程，即在摄像机内、外部参数已标定的情况，将匹配像点的坐标值代入定位模型，从而求解物点的3D坐标，是立体视觉的关键环节。目前的计算方法分为两类［1－2］，即求取投影线交点法和图像校准法。直接求取投影线交点的方法虽然是三维重建计算的传统方法，但在实际中由于成像畸变、图像噪声和对应点匹配误差，物点的左右图像投影的反向延长线很难相交于一点，如果直接将匹配像点的坐标值代入双目视觉定位模型，需要求解的超定方程是一个矛盾方程，只能通过最小二乘法求解空间点的近似位置［3－5］。另外，由于该方法迭代计算过程繁琐，而且还涉及初值估计和局部最小值的问题，所以计算出的物点精度不高。图像校准法虽然为左、右图像中对应点的匹配提供了方便，但在校准过程中涉及坐标变换和图像变换两个计算量较大的过程［6］。而对于左、右图像中需要匹配的标记物的数量较少，且对应关系易于确定的情况，运用图像校准法进行三维重建计算显得繁琐。针对上述两类方法存在的问题，本文以空间任意两点的欧氏距离为基点，利用摄像机成像模型，经理论推导，建立了求取三维重建物点的数学模型，并证实了该算法具有较高的重建精度。

2 建立计算模型

图1表示一个任意结构的双目视觉系统，对于每个摄像机而言，如果光心和像点已知，就可以确定唯一射线，即OrIr、OlIl，在针孔成像模型下，物点必然在此射线上。因此，在理想情况下，两条射线应在物点处相交，由此可以对空间物点进行交汇定位。但是，在现实情况下它们在空间不一定相交，目前常用的方法是取两条投影线的公垂线中点作为视觉重建的场景点［3，5，7－9］。文献［8］、［9］以矩阵求逆的形式给出了求公垂线PcplPcpr中点Pmid的方法，但在实际应用时，由于矩阵求逆计算量大、效率低，因此我们利用两点间欧氏距离最小化的方法来简化计算过程。

图1 非平行轴双目视觉几何结构

设Kl和Kr分别为左右摄像机的内部参数矩阵，即:

R和T分别为右摄像机相对于左摄像机的旋转向量和平移向量，Il(ul，vl)和 Ir(ur，vr)分别为左右图像平面上的一对共轭图像点，根据小孔成像原理，共轭图像点归一化［10］后，其齐次坐标 Nl(Ul，Vl，1)、Nr(Ur，Vr，1)分别为:

设点Pl是投影线OlIl上的任意点，在左摄像机坐标系中的坐标为Pl(Xl，Yl，Zl);同理，点 Pr是投影线OrIr上的任意点，在右摄像机坐标系中的坐标为Pr(Xr，Yr，Zr)，则有:

设点Pr在左摄像机坐标系中的坐标为)，由坐标变换关系可得:

则点Pl和Pr之间的欧氏距离为:

将式(3)～式(6)代入式(8)，得:

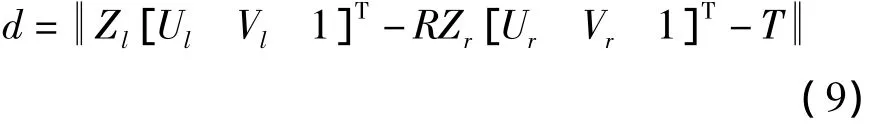
由范数的性质可得:

式中:

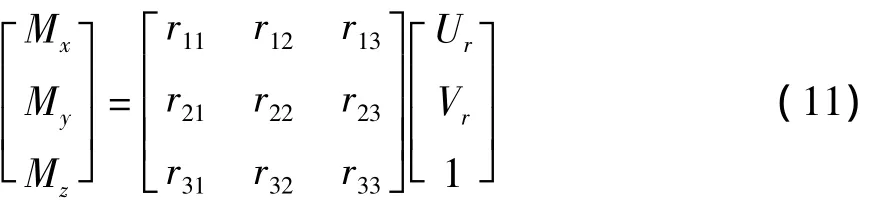
即:

因为d表示的是两点间距离，所以d2存在最小值。

由

可得:

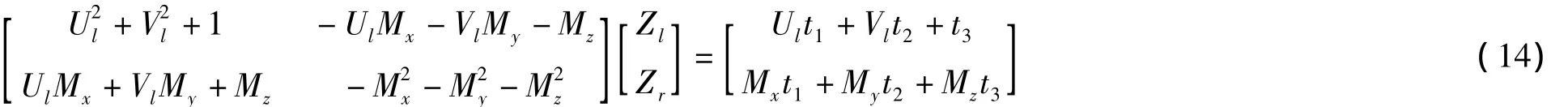
求解式(14)得:

即:

将式(12)代入式(16)得:

此时的Zl、Zr即为公垂线PcplPcpr两端点分别在左右摄像机坐标系中Z轴方向上的坐标值，将式(17)分别代入式(5)、式(6)可得 Pcpl(Xcpl，Ycpl，Zcpl)和 Pcpr(Xcpr，Ycpr，Zcpr)的全部坐标值:

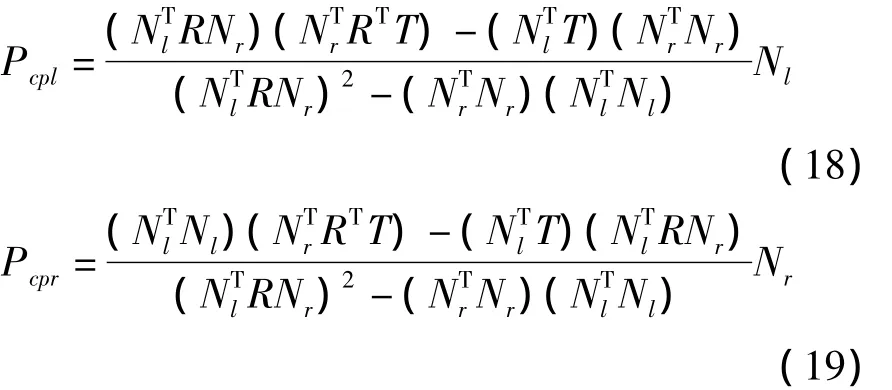
另由式(7)知Pl在右摄像机坐标系中的坐标，因此，如果公垂线中点 Pmid为空间场景点Ps的估计，则它在左、右摄像机坐标系中的坐标分别为:

可见，对于经过标定的双目视觉系统，其内部参数Kl和Kr以及外部参数R和T是已知的。从左右摄像机获取的共轭图像点 Il(ul，vl)和 Ir(ur，vr)，由式(3)、(4)可求出它们的正规化坐标Nl和Nr，再由式(18)、(19)求出两条投影线的公垂线端点Pcpl和Pcpr。最后，通过公式(20)和式(21)求出公垂线中点作为空间物点的三维坐标。

3 实验及结果

图2为自行研制的双目视觉系统实验样机，主要包括双目视觉定位仪、系统标定板、标记点、微型计算机及应用软件等。双目视觉定位仪选用两台像素为1392×1040的DH－SV1420FM黑白工业数字摄像机和高分辨、微畸变的Kowa透镜LM6NCM自制了双目立体视觉传感单元，为扩大测量范围，双目视觉基线长度选定为200 mm。标定好双目视觉参数后，利用自行设计的软件，计算出处于不同位置的标记物的空间坐标，进而得到各标记物之间的距离(测量值)，如图3所示。

标记物1～6为随机打印在A纸上的标记物图案，以游标卡尺测量的各标记物之间距离作为基准值，分别用投影线交点法、图像校准法和本文方法检测标记物，并将各标记物之间距离的测量与基准值相比较，结果如表1所示。

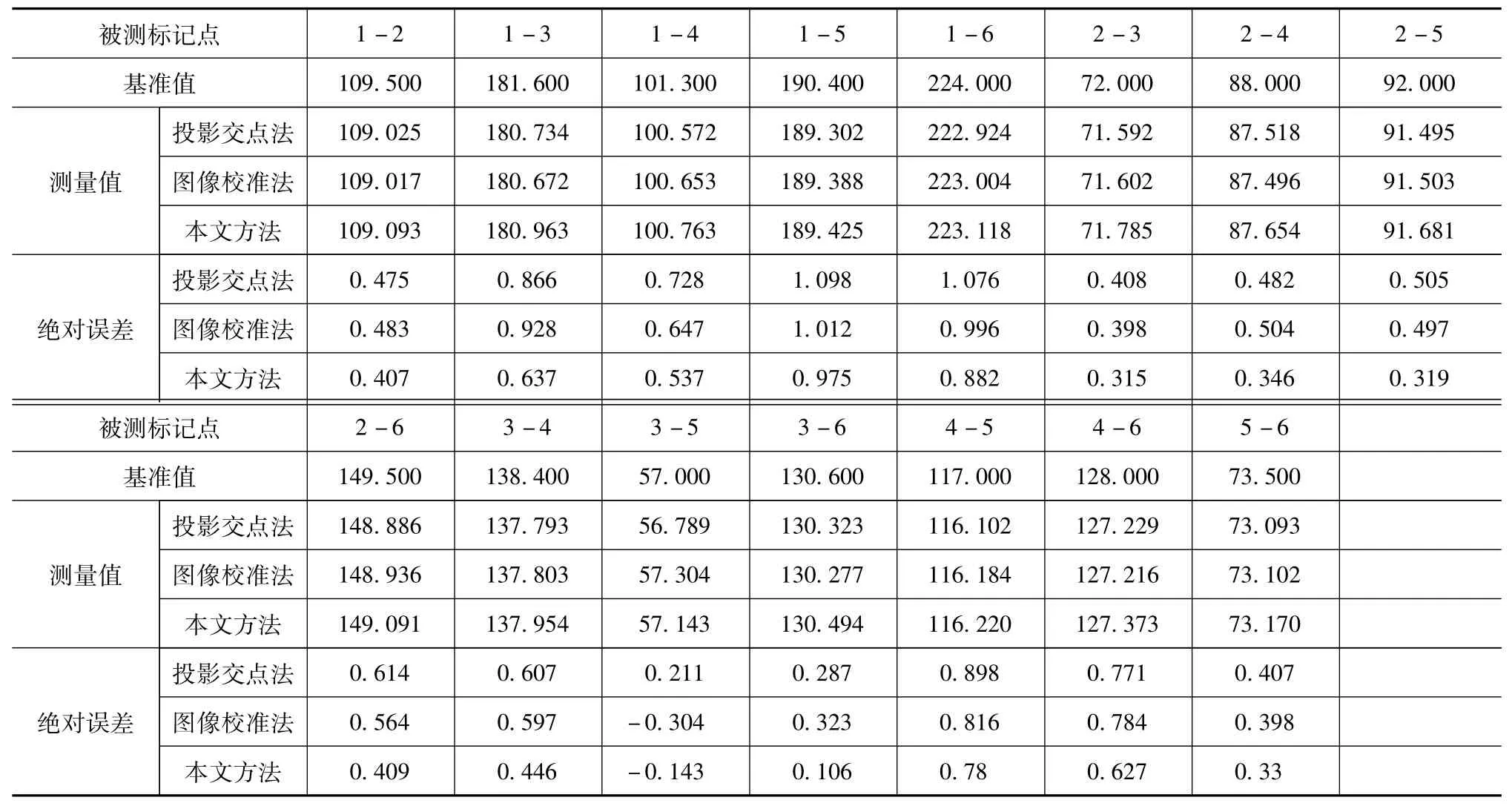
表1 各标记物之间的距离与误差值

为了直观反映三种重建方法的检测精度，作如图4所示的绝对误差折线图。由图可以看出，本文所述的重建算法优于其他两种方法，能够获得较高精度的检测效果，在距立体定位仪1500 mm的前视范围内，空间三维点距离的测量误差不超过±1 mm。

图4 三种重建方法检测标记物间距的误差

4 结束语

本文通过分析直接求取投影线交点法和图像校准法进行三维重建计算的不足，提出了基于欧氏距离最小化的三维重建计算方法，进行了理论推导与实验验证。结果表明:该方法的重建精度高于投影线交点法、图像校准方法，而且避免了矩阵求逆、迭代求解及图像校准等繁琐过程，从而提高了三维重建的实时性。

［1］David A Forsyth，Jean Ponce．Computer Vision:A Modern Approach［M］．Pearson Education Asia Limited and Tsinghua University Press，2004:235 －338．

［2］D Scharstein，R Szeliski．A taxonomy and evaluation of dense two-frame stereo correspondence algorithms［J］．International Journal of Computer Vision，2002，47(1):7 －42．

［3］Luo Shimin，Li Maoxi．Research on how to get object＇s 3D coordinate on two CCD camera measure system［J］．Computer Engineering and Design，2006，27(19):3622 －3624．(in Chinese)罗世民，李茂西．双目视觉测量中三维坐标的求取方法研究［J］．计算机工程与设计，2006，27(19):3622－3624．

［4］Hu Yingfeng．Research on the 3D reconstruction method based on scale-invariant feature transform feature matching algorithm［J］．Process Automation Instrumentation，2011，32(1):30 －32．(in Chinese)胡影峰．基于SIFT特征匹配算子的三维重建方法研究［J］．自动化仪表，2011，32(1):30 －32．

［5］Fu Qiang，Wang Chunping．New algorithm for three-dimensional construction of point object［J］．Science Technology end Engineering，2008，8(3):643 －647．(in Chinese)付强，王春平．一种点目标三维重构的新算法［J］．科学技术与工程，2008，8(3):643 －647．

［6］Wang Weiqiang，Xu Jin，Du Xin，et al．Long range 3D reconstruction based on wide baseline stereo vision［J］．Journal of Zhejiang University:Engineering Science，2010，44(6):1073 －1078．(in Chinese)王炜强，徐进，杜歆，等．基于宽基线立体视觉的远距离三维重构［J］．浙江大学学报:工学版，2010，44(6):1073－1078．

［7］Emanuele Trucco，Alessandro Verri．Introductory techniques for 3-D computer vision［M］．Prentice Hall，1998:161－171．

［8］R Elias．Projective geometry for three-dimensional computer vision［J］．Proceedings of Seventh World Multiconference on Systemics，Cybernetics and Informatics，SCI＇03，2003，5:99 －104．

［9］Beardsley P A，Zisserman A，Murray D W．Sequential updating of projective and affine structure from motion［J］．International Journal of Computer Vision，1997，23(3):235－259．

［10］ Ma Songde，Zhang Zhengyou．Computer vision［M］．Beijing:Science Press，1998:52 －60．(in Chinese)马颂德，张正友．计算机视觉［M］．北京:科学出版社，1998:52－60．