钢筒内衬爆炸水井设计中的几个动力学问题研究

顾文彬，陈学平，刘建青

（中国人民解放军理工大学野战工程学院，南京 210007）

1 前言

随着水下兵器技术的发展，水中爆炸载荷研究与试验、水中爆炸冲击波与目标的毁伤作用研究、新型炸药威力参数测定以及水下弹药威力评估研究，急需不同尺寸和不同结构形式的爆炸水池与爆炸水井的设计与建设。国内多个高校和军工研究机构以及大型企业甚至部队都建造了一些水下爆炸研究设施。国内外的设计师们通常采用基于静态力学理论的工程设计方法，安全系数一般都很高，但不能详细分析和评估爆炸水井或水池实际应用中的动力学响应，以及受力变形薄弱环节与形成机理。采用非线性爆炸动力学理论与数值模拟技术设计爆炸水井或水池等试验设施，可以得到不同设计指标要求下，既满足强度安全性要求又可获得较小结构尺寸的优化结构方案。因此，采用数值模拟手段的爆炸动力学仿真设计方法是对工程设计理论的发展，具有重要理论和应用价值。

2 计算模型与参数

2.1 力学模型及参数

该模型由一个以带底圆钢筒为内衬、以素混凝土为围堰的爆炸水井，水池内的水和试验用装药等组成，其简化模型如图1所示。爆炸水井的内径和深度均为11 m；钢筒内衬为15MnV合金钢材料，壁厚为20～50 mm；围堰为C40素混凝土材料，厚度为300～500 mm；底座也为C40素混凝土材料，其厚度取2 m；装药为球形2，4，6-三硝基甲苯（TNT）炸药，取最大质量3 kg为设计依据。本文仅以装药在水井中心处爆炸情况开展仿真计算和动力学分析。因此，本文计算模型中主要包含5种材料，分别为15MnV合金钢钢筒、钢筒中的水、TNT炸药、空气以及素混凝土。

图1 内衬钢筒混凝土爆炸水井示意图Fig.1 Sketch of the explosion water-well with steel-inner

采用TrueGrid软件建立模型，其中炸药区域采用在k文件中填充的方式加入。模型中水、炸药和空气采用欧拉网格划分，混凝土围堰和钢板圆筒采用拉格朗日网格划分，采用流固耦合算法，其中空气施加透射边界，并在混凝土底座底部定义Z（水深）方向刚性约束。

2.2 材料模型及参数

TNT炸药采用Mat_High_Explosive_Burn材料模型和JWL状态方程，p-V关系如式（1）所示

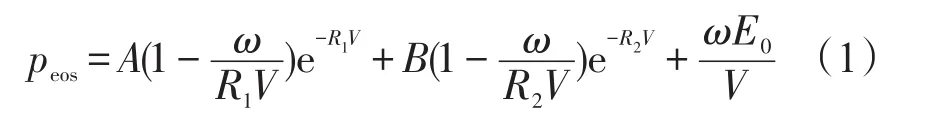
式（1）中，peos为爆轰产物压力；A、B、R1、R2、ω为试验确定的常数；V为相对体积；E0为初始内能。具体参数如表1所示[1]，表1中D0为炸药爆速；pCJ为炸药爆炸产生的爆轰波C-J面压力；ρ为炸药密度。

表1 TNT炸药材料参数Table 1 Explosive material parameters of TNT

混凝土采用Plastic-Kinematic模型，随动硬化系数β=0.5。屈服强度计算公式为[2]

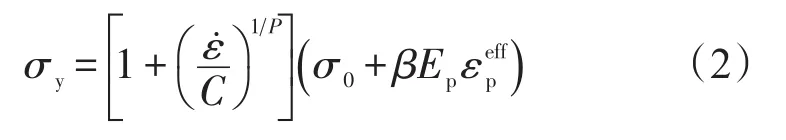
式（2）中，σy为屈服强度；ε为加载应变率；C、P为与材料类型有关的常数；为有效塑形应变；β为随动硬化系数；σ0为初始屈服强度；Ep为塑形硬化模量。具体材料参数列于表2[3]，表2中，E为弹性模量；Et为剪切弹性模量；σs为材料的弹性屈服强度。

表2 混凝土材料参数Table 2 Material parameters of concrete

钢筒筒体也采用Plastic-Kinematic模型，材料参数如表3所示[4]。其弹性屈服强度极限为333～412 MPa，计算时取σs=337 MPa，塑性屈服强度极限为490 ～ 549 MPa，计算时取σb=519.5 MPa[5]。

表3 钢筒筒体材料参数Table 3 Material parameters of steel-inner

计算模型中空气采用空物质材料本构模型，状态方程形式为

式（3）中，p为压力；C1，…，C6为常数；μ为体积应变参数，，其中V为相对体积；E0为初始能量[1]。

水状态方程形式如下

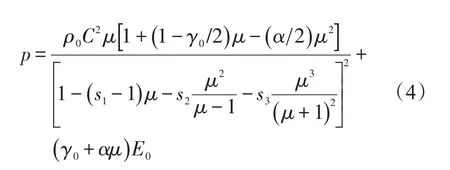
式（4）中，p为压力；ρ0为材料初始密度；C为νs-νp曲线斜率的系数；γ0为Gruneisen常数；α为γ0和μ的体积修正量；E0为单位体积初始能量。参数列于表4[1]。

表4 水的材料参数Table 4 Material parameters of water

3 水中爆炸冲击波压力仿真结果分析

在大量理论和试验研究基础上，前人总结了一些水中爆炸冲击波参数的计算模型。应用最广的是P.Cole关于无限水中爆炸冲击波峰值压力计算公式如下

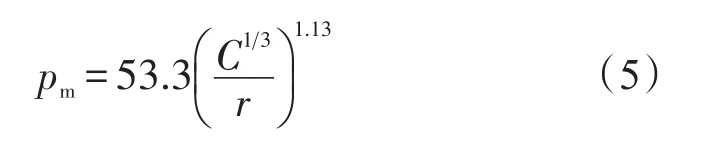
式（5）中，r为装药中心距测点的距离，m；pm为测点r处的冲击波峰值压力，MPa；C为炸药质量，kg。公式（5）适用范围为(20～200)r0，r0为装药半径[6]。

数值模拟得到了筒壁厚度分别为20 mm、25 mm、30 mm和40 mm的爆炸水井中与装药中心等高、距离装药中心分别为250 cm、350 cm、450 cm和525 cm处的冲击波峰值压力（见表5）。由表5可知，对于不同壁厚的爆炸水井，相同水中位置的冲击波压力峰值基本相同。表6是表5所示不同位置冲击波峰值压力数值计算结果平均值与P.Cole公式计算值对比，数值模拟结果与公式计算相对值误差小于±10%，表明水中爆炸冲击波作用的计算模型和参数可信，计算结果正确，满足计算精度要求。

表5 不同筒体壁厚水平方向水中冲击波峰值压力计算结果对比Table 5 The comparison of calculation results of underwater shock wave peak pressure in horizontal direction of different steel-inner wall thicknesses

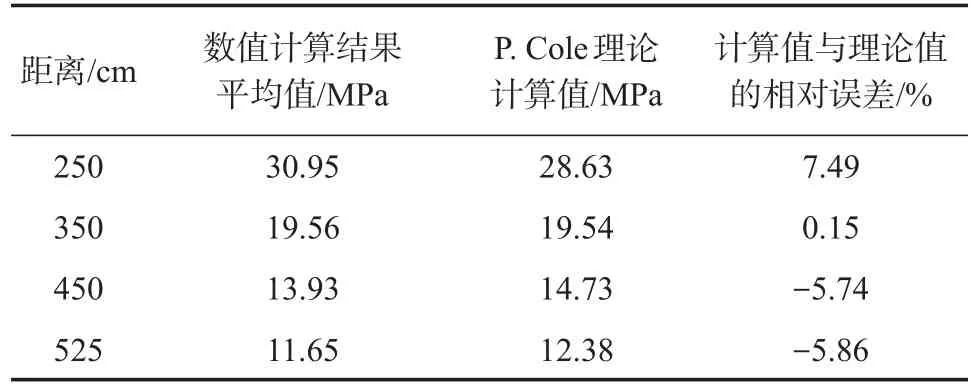
表6 水平方向不同距离水中冲击波峰值压力计算与理论值对比Table 6 The comparison of calculated peak pressure and the theoretical value of underwater shock wave in horizontal direction at different distances

4 钢筒水井爆炸动力学响应数值模拟研究

4.1 水中爆炸作用下钢筒水井应力响应分析

对炸药在壁厚分别为20 mm、25 mm、30 mm和40 mm的水罐中心处的爆炸作用进行了数值模拟，得到了沿筒体筒壁深度方向上、不同测点处筒体单元的Von-Miss等效应力峰值σV-M计算结果（见表7）。由表7可知，当筒壁厚度b=20 mm时，σV-M的最大值出现筒壁中心Z=0 m处，其值为348.9 MPa；当b=25 mm时，σV-M的最大值出现筒壁中心以下Z=-3.9 m处，其值为349.6 MPa；当b=30 mm时，σV-M最大值也发生在Z=-3.9m处，其值为349.3MPa；当b=40 mm时，σV-M最大值仍然发生在Z=-3.9 m处，其值为349.2MPa。可见，σV-M最大值位于Z=0 m和Z=-3.9 m处。因此，Z=0 m和Z=-3.9 m处的受力大小和变化规律对爆炸水井的安全性影响至关重要。

图2是b=25 mm、30 mm和40 mm情况下，仿真得到的Z=0 m处σV-M、σ1和τ1随时间变化的曲线。由图2可知，Z=0 m处σV-M、σ1和τ1随b增加呈现减小趋势，但变化很小。考虑数值计算结果的散布效应，可以用表7所示的4个计算值的算术平均值表示筒壁中心的等效应力峰值，即σˉV-M=348.6 MPa，σˉ1=359.2 MPa和τˉ1=184.1 MPa，这些值均可作为筒体强度的判断依据。由图2还可以发现，σ1和τ1在筒壁上的作用时间随筒体壁厚增加明显减小，这对筒壁的变形累积效应有重要影响。

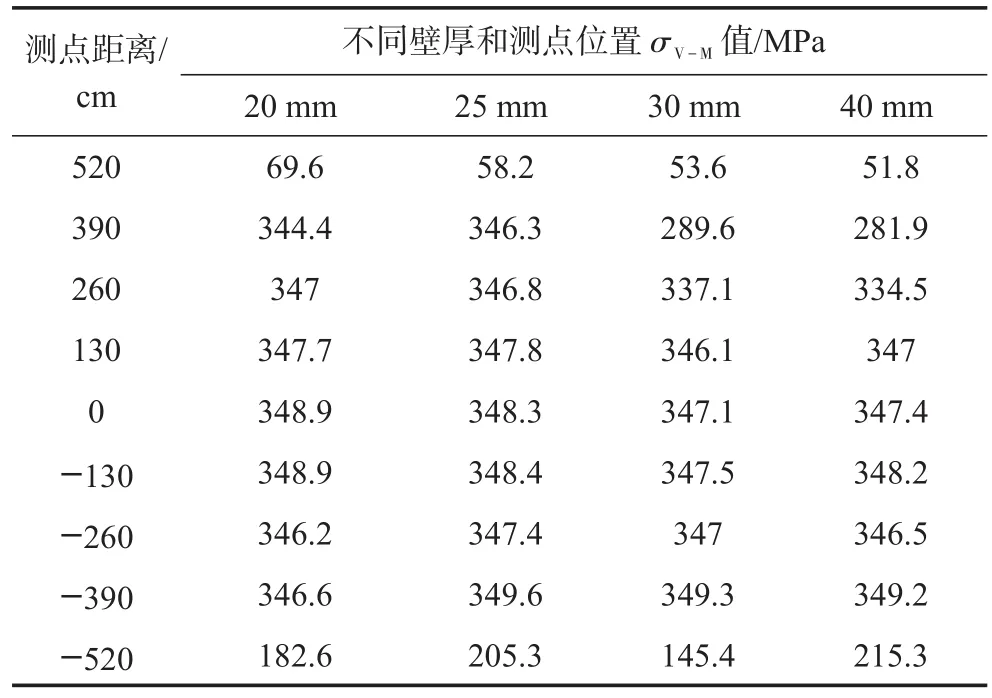
表7 装药在不同壁厚筒体中爆炸不同单元等效应力峰值计算结果对比Table 7 The comparison of calculation results of peak equivalent stress of the charge explosion in different units of different cylinder wall thicknesses

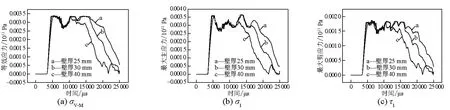
图2 不同壁厚筒壁中心处σV-M、σ1和τ1时程曲线Fig.2 Time history curves ofσV-M，σ1and τ1at Z=0 m of different wall thicknesses

图3是b=25 mm、30 mm和40 mm情况下，仿真得到的Z=-3.9 m处σV-M、σ1和τ1随时间变化的曲线。由图3可知，对于不同筒体壁厚，对应于Z=-3.9 m处σV-M、σ1和τ1峰值差别不大，以σV-M为例，分别为349.6 MPa、349.3 MPa和349.2 MPa（见表7）。Z=-3.9 m处的σ1和τ1峰值也具有峰值应力相差不大的特点。随着筒体壁厚的增加，上述特征应力作用时间明显减小。因此，可以用Z=-3.9 m处σV-M、σ1和τ1的峰值平均值作为筒体下部强度判断依据。根据仿真结果，σˉV-M=349.4 MPa，σˉ1=375.6 MPa和τˉ1=188.8 MPa。

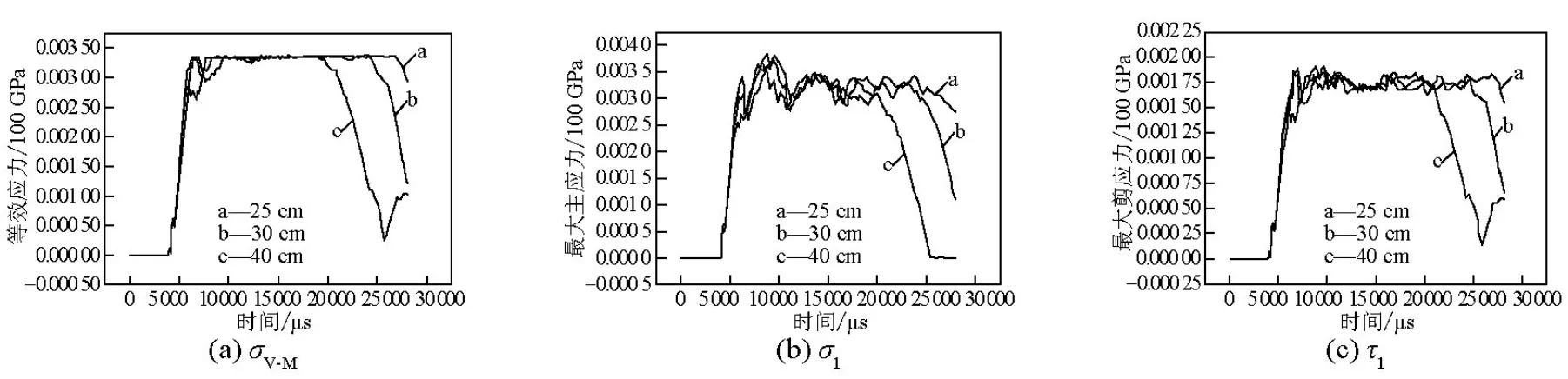
图3 不同壁厚Z=-3.9 m处σV-M、σ1和τ1时程曲线Fig.3 Time history curves ofσV-M，σ1andτ1at Z=-3.9 m of different wall thicknesses

4.2 水中爆炸作用下钢筒水井应变响应分析

图4和图5分别是不同壁厚爆炸水井筒壁中心处，计算得到的等效应变εeff时程变化曲线和等效塑性应变时程变化曲线。由图4可知，随着b的增大，εeff峰值显著下降，从b=25 mm的0.00291下降到b=40 mm的0.00159。而且，随着筒壁上爆炸冲击波作用载荷的衰减，由于筒壁材料的弹性恢复，值不断下降。计算结果显示，爆炸作用后的25 ms时刻，对应于b=25 mm、30 mm和40 mm，在爆炸水井筒体中心处的分别为0.00175、0.00099和0.00019。图5中所示结果表明，3 kg TNT炸药爆炸条件下，3种壁厚的爆炸水井都产生了一定的塑性变形，即使b=40 mm时筒壁仍有0.00019的等效塑性应变。可见，随着筒壁厚度的增加，水中爆炸冲击波作用下筒体塑性应变快速降低，但要完全消除塑性变形，筒壁厚度还需继续增加。

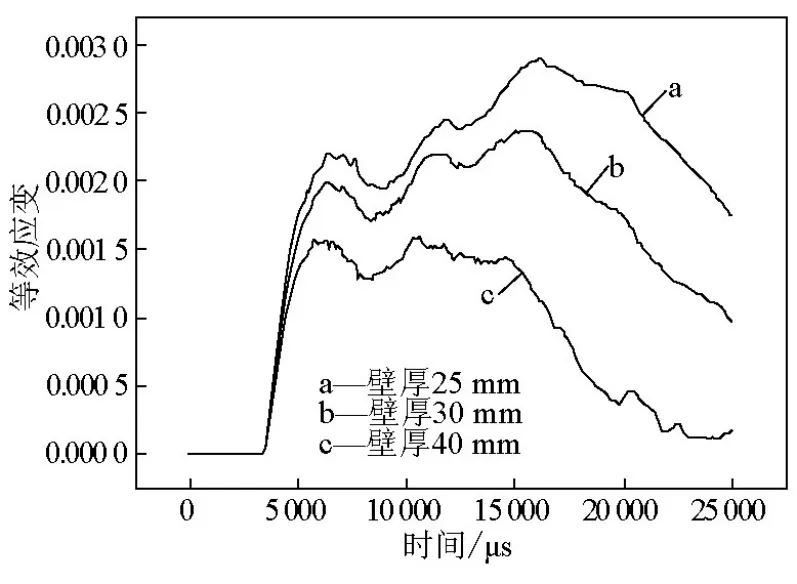
图4 不同壁厚筒体中心εeff时程曲线Fig.4 Time history curves ofεeffat Z=0 m of different wall thicknesses

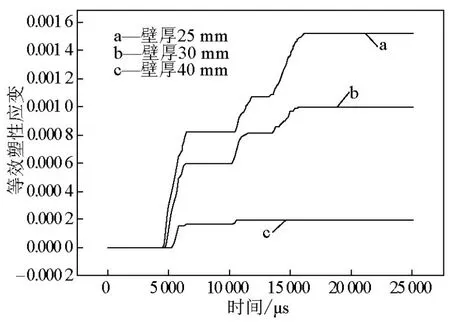
图5 不同壁厚筒体中心时程曲线Fig.5 Time history curves ofat the center of different wall thicknesses

图6和图7分别是不同壁厚筒体上Z=-3.9 m处εeff和时程变化规律对比。由图6和图7可知，直到40 mm壁厚情况下，该部位无论是εeff还是的数值都很大，特别是表征残余变形的等效塑性应变值很大，都达到0.002以上。依据最大伸长线性应变理论，这样的应变水平不满足安全性设计要求。

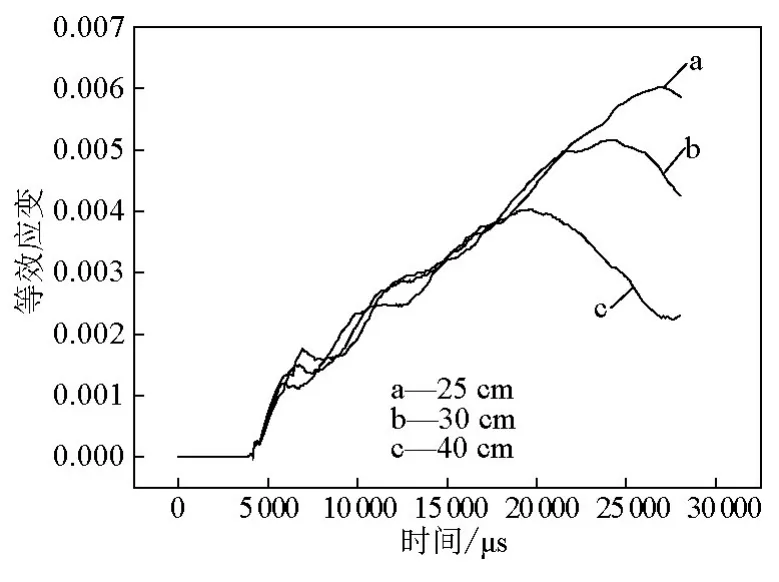
图6 不同壁厚-3.9 m处εeff时程曲线Fig.6 Time history curves ofεeffat Z=-3.9 m of different wall thicknesses

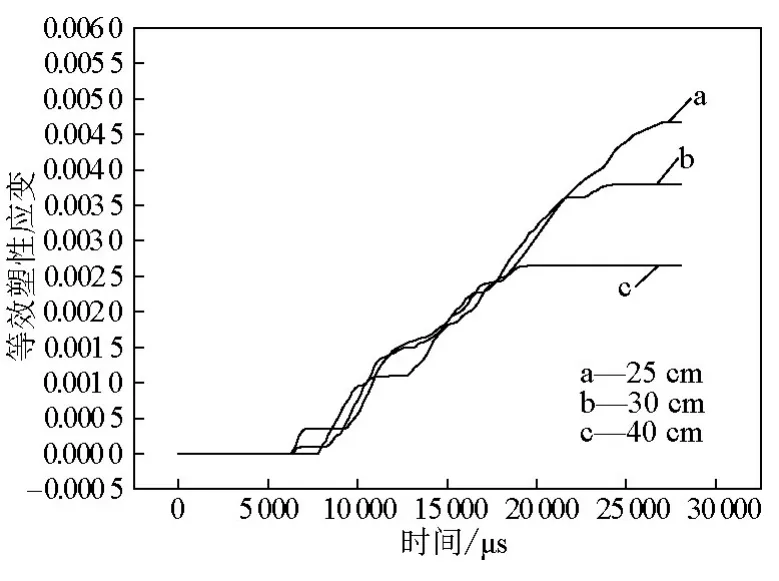
图7 不同壁厚-3.9 m处时程曲线Fig.7 Time history curves ofat Z=-3.9 m of different wall thicknesses

图8是计算得到的筒体从25 mm到50 mm的4个壁厚条件下沿筒壁深度方向Z=-5.25～-2.5 m范围内连续变化的分布曲线。以大于0.002为屈服判断条件，图8中用水平虚直线代表0.002塑性应变状态。由图8可知，随着筒体壁厚的增加，爆炸水井产生塑性变形失效的区域逐渐变小，峰值也逐渐降低。当塑性变形失效区域确定后，设计时可以根据不同壁厚筒体变形失效范围的大小，采用局部加强的措施来满足安全性强度设计要求。因此，图8所示分析结果对爆炸水池结构尺寸设计有重要参考价值。根据数值计算结果，当b=25 mm时，失效变形的区域为-4.8～-2.86 m，最大值出现在-4.1 m处，对应值为0.00472，需要加强的高度为2 m；当b=30 mm时，失效变形的区域为-4.75～-3.38 m，最大值出现在-4.15 m处，对应峰值下降为0.004，需要加强的高度为1.37 m；当壁厚为40 mm时，失效变形区域为-4.6～-3.64 m，最大值出现在-4.15 m处，对应峰值下降为0.0028，需要加强的高度为0.96 m。

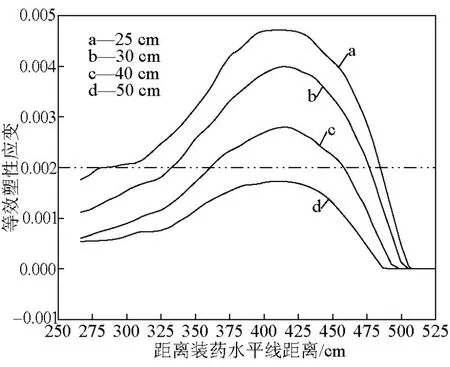
图8 不同壁厚筒体时程曲线对比Fig.8 The comparison of time history curves ofof different wall thicknesses

图8还表明，当b=50 mm时，εpeff最大值为0.0016，发生在Z=-4.1 m处，但该值小于0.002的拉伸断裂失效判断条件。据此可以认为，3 kg TNT炸药爆炸条件下，50 mm壁厚的钢筒爆炸水井不会发生拉伸断裂，但仍不满足强度设计要求。

5 内衬钢筒的混凝土围堰水井爆炸动力学响应数值模拟研究

上述研究表明，直到b=50 mm时筒体仍有最大可达0.0016的等效塑性应变，严格意义上讲仍不满足弹性屈服安全性设计要求。另一方面，如此厚度的大直径和大深度钢筒加工与运输及安装难度都很大，建造成本也非常高。为此，工程上通常采用薄钢板圆筒外增加一定厚度混凝土围堰的办法，设计成钢筒内衬加混凝土围堰的爆炸水井。下文针对钢筒壁厚20 mm、3 kg TNT装药爆炸时，设计满足安全性要求的混凝土围堰厚度。

分别对混凝土围堰厚度B=400 mm、500 mm的两种情况进行仿真计算，得到钢筒内衬深度方向不同位置处εeff和峰值的计算结果，如表8所示。由表8可知，当B=400 mm时，在钢筒内壁中心以下2.6 m处仍产生塑性变形，峰值仅为0.00012。这是因为该处的σeff=347.13 MPa，仍大于弹性屈服极限值。当B=500 mm时，表8所示表明钢筒内衬深度方向峰值均为0，即钢筒内衬未出现塑性变形。

表8 不同厚度混凝土围堰等效应变与等效塑性应变仿真结果Table 8 The simulation results of equivalent strain and equivalent plastic strain of different concrete cofferdam thicknesses

图9是B=400 mm、500 mm时，Z=-2.6 m处钢筒内壁上σV-M、σ1和τ1时程曲线对比图。由图9可知，随着混凝土围堰厚度的增加，爆炸水井的钢筒内壁上σV-M、σ1和τ1峰值逐渐降低，σV-M值由347.13MPa下降到321.52 MPa，σ1值由332.42 MPa下降到292.38 MPa，τ1值由194.87 MPa下降到177.91 MPa。

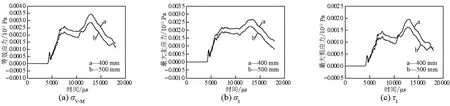
图9 不同围堰厚度钢筒内壁Z=-2.6 m处σV-M、σ1和τ1时程曲线对比Fig.9 The comparison of time history curves ofσV-M，σ1andτ1at Z=-2.6 m of steel inner wall of different concrete cofferdam thicknesses

因此，无论是根据第三还是第四强度理论，当钢筒内衬壁厚20 mm、混凝土围堰厚度为500 mm时，内衬钢筒的混凝土爆炸水井结构均满足安全性设计要求。

6 气泡帷幕对提高爆炸水井安全性响应的数值模拟研究

在炸点和保护目标之间设置气泡帷幕来衰减冲击波是水下爆破施工中常用的安全性防护措施。在爆炸水井中设置气泡帷幕，不仅可以提高试验设施的抗爆安全性，在满足安全性强度设计要求的前提下，还可减小水井筒壁厚度，降低建设成本。下文将研究在水井底部设置半径为4.9 m、厚度为0.05 m气泡帷幕时，钢筒壁厚仍为20 mm、3 kg TNT装药水井中心爆炸条件下，满足强度要求的爆炸水井混凝土围堰厚度的设计。

表9是爆炸水井内是否设置气泡帷幕情况下，距装药中心不同水平距离处冲击波压力峰值计算的结果对比。由表9可知，对于距装药中心水平距离均为5.25m处的测点，不设置气泡帷幕时的pm=12.88MPa，而设置气泡帷幕时的pm=7.65 MPa，冲击波压力峰值衰减了40.6%。文献[4] 给出的试验结果表明，气泡帷幕可使冲击波峰压衰减50%以上[7-9]。

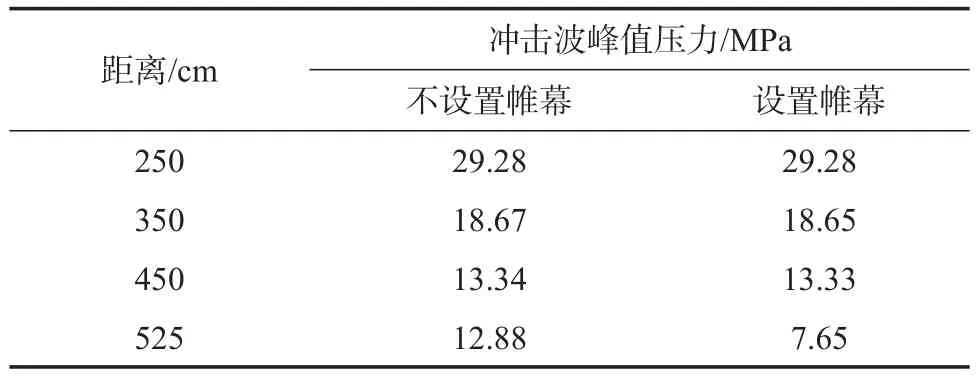
表9 气泡帷幕对水中冲击波峰值压力影响的仿真结果对比Table 9 The comparison of bubble curtain on the simulation results of underwater shock wave peak pressure

图10和图11为两种情况下水平距离为5.25 m处的压力时程曲线。对图中p～t曲线积分得到测点处的冲量。比较冲量计算结果表明，测点处不设置气泡帷幕时的冲量i=0.0337 MPa·s，而设置气泡帷幕时的冲量i=0.0317 MPa·s，冲量值仅衰减了6%。因此设置气泡帷幕对冲量的衰减作用有限。

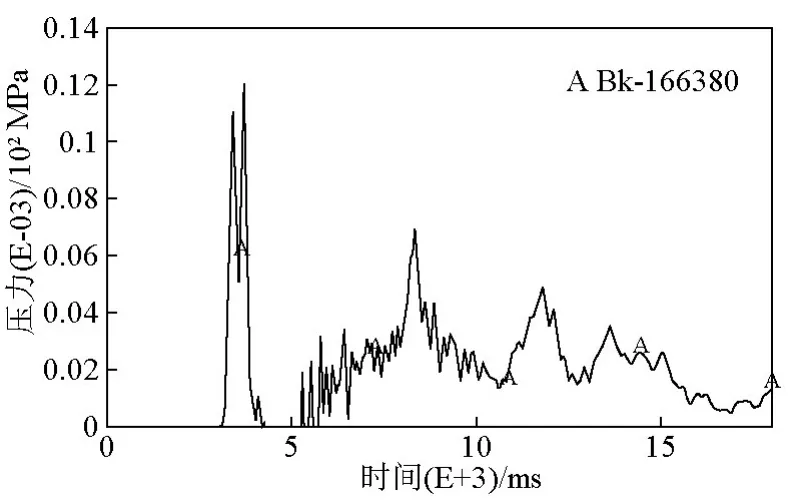
图10 不设置气泡帷幕压力时程曲线Fig.10 The time history curves of pressure without bubble curtain

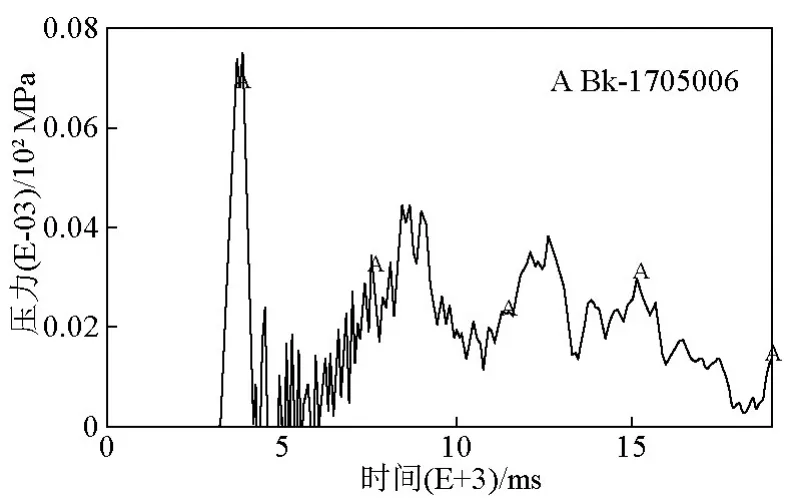
图11 设置气泡帷幕压力时程曲线Fig.11 The time history curves of pressure with bubble curtain

在设置气泡帷幕的情况下，分别对混凝土围堰厚度为300 mm、350 mm两种情况进行仿真计算，得到钢筒内衬深度方向不同位置εeff和峰值计算结果（见表10）。由表10可知，当B=300 mm时，在Z=-2.6 m处钢筒内壁仍产生塑性变形，峰值仅为0.00016；当B=350 mm时，钢筒内衬深度方向峰值均为0，即钢筒内衬未出现塑性变形。

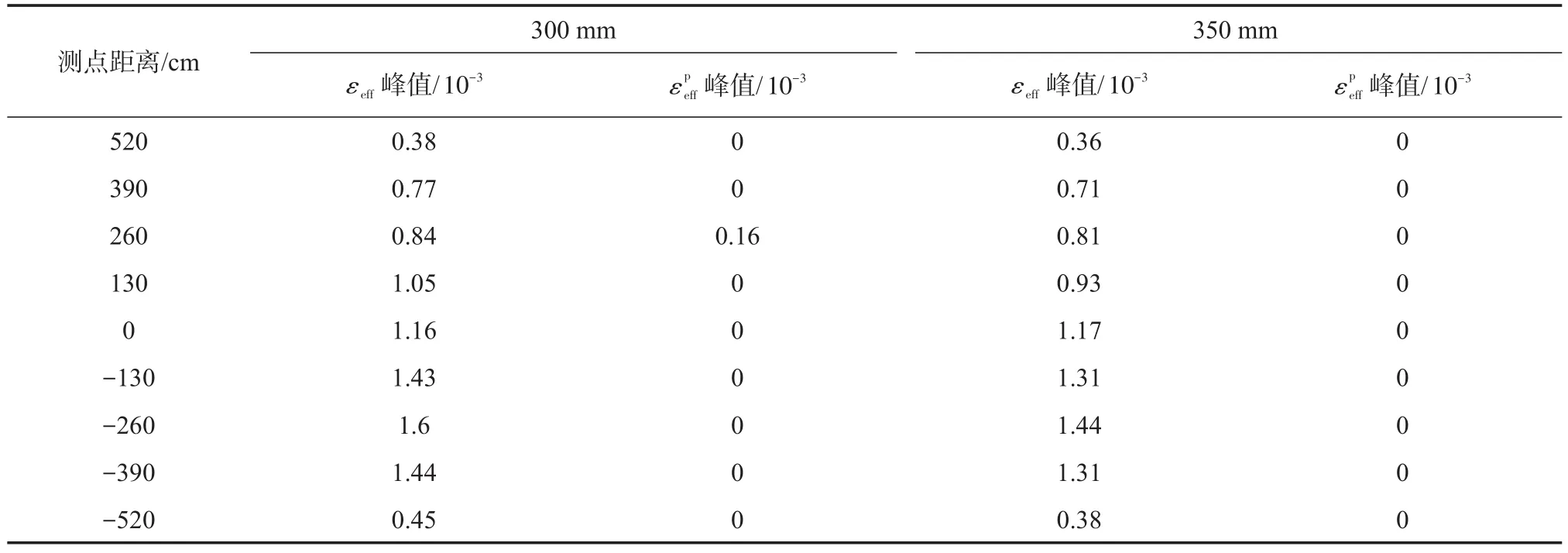
表10 不同厚度混凝土围堰等效应变与等效塑性应变仿真结果Table 10 The simulation results of equivalent strain and equivalent plastic strain of different concrete cofferdam thicknesses under the condition of bubble curtain

图12是B=300 mm、350 mm、400 mm时，设置气泡帷幕情况下，Z=-2.6 m处钢筒内壁上σV-M、σ1和τ1时程曲线对比图。由图12可知，随着混凝土围堰厚度的增加，爆炸水井的钢筒内壁上σV-M、σ1和τ1峰值逐渐降低，σV-M值由B=300 mm时的346.70 MPa下降到B=350 mm时的331.13 MPa，再降到B=400mm时的300.95MPa，σ1值由346.59MPa下降到 320.23 MPa，再降到 300.95 MPa，τ1值由191.54 MPa下降到181.41 MPa再降到167.80 MPa。这表明：当混凝土围堰厚度增加到350 mm时，爆炸水井钢筒内壁满足弹性屈服强度设计要求。因此，无论是根据第三还是第四强度理论，当钢筒内衬壁厚为20 mm、设置气泡帷幕、混凝土围堰厚度为350 mm时，内衬钢筒的混凝土爆炸水井结构即可满足安全性设计要求[10]。

图12 气泡帷幕情况下不同围堰厚度钢筒内壁Z=-2.6 m处σV-M、σ1和τ1时程曲线对比图Fig.12 The comparison of time history curves ofσV-M，σ1andτ1at Z=-2.6 m of steel inner wall of different concrete cofferdam thicknesses under the condition of bubble curtain

7 结语

通过对单一钢筒爆炸水井、内衬钢筒混凝土围堰爆炸水井以及内置气泡帷幕爆炸水井爆炸作用过程的数值模拟研究，得出如下结论。

1）炸药在钢筒水井中爆炸时，随着筒壁厚度的增加，筒体上应力应变峰值逐渐下降，处于高应力状态的时间逐渐减小，从而增强了钢罐水井的抗变形能力。当壁厚增加到50 mm时，钢筒水井上等效塑性应变最大值为0.0016，不满足强度设计要求，由此可知单从增加筒壁厚度出发是不可取的。

2）由于筒壁内应力波传播、叠加与反射作用以及冲击波的相互作用，钢筒上恶劣的应力应变区域总是出现在装药中心以下的筒底附近。随着壁厚的增加，筒体上高应力状态和大变形区域的带宽逐渐减小，这对钢筒爆炸水井薄弱部位探查和局部加强设计提供了依据。

3）采用20 mm薄钢板圆筒外增加混凝土围堰而设计的内衬钢筒混凝土爆炸水井时，C40混凝土层厚度大于500 mm就可满足弹性屈服安全性设计要求。

4）在内衬钢筒混凝土爆炸水井内设置气泡帷幕时，气体帷幕对水中爆炸冲击波压力峰值的衰减能力不低于40%、冲量的衰减能力约为6%，能有效改善爆炸水井的抗爆性能。在满足强度设计要求的前提下，爆炸水井的混凝土围堰厚度可减小到350 mm，进一步节约了建造成本。

[1] 时党勇，李裕春，张国民.基于ANSYS/LS-DYNA8.1进行显示动力分析[M] .北京：清华大学出版社，2002.

[2] LSTC.LS-DYNA keyword user’s manual[R] .California：Livermore Software Technology Corporation，2003.

[3] 肖绍清，王文杰，曹桂祥，等.炮孔复合装药结构对混凝土作用的数值模拟研究[J] .工程爆破，2003，9（3）：19-21.

[4] 张秀华，张春巍，段忠东.爆炸荷载作用下钢框架柱冲击响应与破坏模式的数值模拟研究[J] .沈阳建筑大学学报，2009，25（4）：656-661.

[5] 张祖贤，邢安定，汪 熹，等.兵器黑色金属材料手册[M] .北京：兵器工业出版社，1990.

[6] P.库尔（美）.水下爆炸[M] .北京：国防工业出版社，1960.

[7] 樊自建，沈兆武，马宏昊.水中空气隔层对冲击波传播衰减作用的初步探讨[J] .工程爆破，2007，13（2）：7-10.

[8] 张志波，李春军，李红勇，等.气泡帷幕在水下爆破减震工程中的应用[J] .爆破，2003，20（2）：75-76.

[9] 周 睿，冯顺山.气泡帷幕对水中冲击波峰值压力衰减特性的研究[J] .工程爆破，2001，7（2）：13-17.

[10] 徐秉业，刘信声.应用弹塑性力学[M] .北京：清华大学出版社，1995.