串列双方柱绕流的数值模拟

吕启兵，杨 斌，杨忠超，李鹏浩

(1.重庆交通大学河海学院，重庆400074;2.温州港集团有限公司，浙江温州325100)

钝体绕流问题广泛存在于桥梁、海洋港口、航空航天、交通运输等工程科学领域，如置于水中的桥墩、石油钻井平台的墩柱、港口码头的桩柱、飞机机翼绕流、汽车的风阻等。而方柱作为一种典型的钝体，一直是流体力学领域绕流问题的热点之一。关于方柱绕流问题的实验研究也已经进行得相当广泛，许多研究者通过各种方法对方柱的绕流进行了实验模拟研究，D.A.Lyn，等［1-2］提供了大量的实验模拟资料，为实际的工程问题提供了一定的参考。

随着计算机计算能力的提升、数值算法的改进与计算流体力学(CFD)的突飞猛进，数值模拟技术已成为钝体绕流问题研究的一种有效手段，桩柱绕流问题的数值模拟也得到了很大的发展。早期的Hiromasa Kawai，等［3］对雷诺数为 200 的串列方柱的绕流用差分方法做了数值模拟;王远成，等［4］人采用湍流RNG k-ε模型对钝体绕流流场的不稳定、非定常流动进行了数值模拟;S.Muralami，等［5］使用标准k-ε模型对钝体绕流进行了研究，并且利用了大涡模型(LES)进行了数值计算;陈素琴，等［6］数值模拟了雷诺数为10 000情况下两串列方柱绕流的干扰问题，并分析了不同间距下各方柱的升阻力特征及流场特性。

由于内河特殊的水文环境(大水位差变化与较大的流速)，近年来内河码头运用全直柱框架结构作为一种新的码头结构型式，在考虑施工过程、工程条件与经济因素等方面时，全直桩方柱框架码头已十分普遍。笔者利用流体软件、采用RNG k-ε模型对串联双方柱绕流进行了数值模拟，分析了每根柱升、阻力特性与不同桩距下的流场演变情况，为实际工程问题提供一定参考。

1 数值模型与模型验证

1.1 控制方程

对于不可压缩黏性流体，在直角坐标系下，流体的运动可用Navier-Stokes方程［7］与动量方程描述：

模拟计算采用RNG k-ε模型，该模型由Yakhot和Orzag提出，模型是从瞬态N-S方程中推出的，通过大尺度运动和修正后的黏度项体现小尺度的影响，而使这些小尺度运动有系统地从控制方程中去除，所得到的k方程和ε方程与标准k-ε模型非常相似：

式中：Gk是由层流速度梯度产生的湍流动能k的产生项C1ε=1.44，η。=4.377，β =0.012，C2ε=1.68;ε 为湍动耗散率。

RNG k-ε模型来源于严格的统计技术，是对标准k-ε模型的重要改进。RNG模型在ε方程中加入了一个Rε条件，从而反映了主流的时均应变率Eij，这样该模型中产生项不仅与流动情况有关，而且在同一问题中也还是空间坐标的函数，从而可以更好的处理高应变率及流线弯曲程度较大的流动。

1.2 数值算法

计算区域网格采用分块结构化网格(图1)，网格总量在4.9万～18.9万之间，利用有限体积法(FVM)对方程进行离散，压力基求解器与压力2阶离散格式，动量、湍动能和湍动耗散率选项全部为2阶迎风格式，计算模型选用RNG k-ε模型，PISO算法。

1.3 边界条件

进口边界条件：u=1，v=0。

出口边界条件：自由出流。

上下边界及方柱表面为壁面边界条件，即u=0，v=0的无滑移边界条件。

雷诺数：Re=UD/υ=22 000。式中：U为来流流速;D为方柱边长;υ为流体的动力黏性系数。

1.4 计算区域与网格划分

计算区域如图1，单柱计算区域为22D×13D(D为方柱边长)，距入口边界距离6D，考虑上下边界对方柱周围流场的影响，上下边界距方柱都为6D，与出口距离为15D;双方柱间距为L，其余设置与单方柱相同。

图1 单方柱与双方柱计算区域与网格Fig.1 Calculation area and grid of single square cylinder and double square cylinder

1.5 模型验证

方柱绕流常用于模拟研究流体的荷载，即对建筑物和构筑物的阻力、升力和柱上涡街脱落频率。为了验证数值模拟的准确性，首先计算了Re=22 000情况下的单方柱绕流问题。方柱上阻力系数、升力系数与斯特罗哈数的定义为：

式中：Fd为阻力，Fl为升力，u为来流流速，D为方柱边长，f为涡街脱落频率，即方柱上涡街的脱落频率，、Cl分别代表阻力系数均值与升力系数。

从表1可以看出，模拟计算结果与 D.A.Lyn，等［1-2］试验结果非常接近，模拟计算误差在7%以内，模拟得到的单方柱情形下的升、阻力系数如图2。

表1 单方柱绕流模拟计算结果比较Table 1 Comparison results of flow around square cylinder simulation

图2 Re=22 000时单方柱升、阻力系数Fig.2 Lift and drag coefficients of single square cylinder when Re=22 000

2 模拟结果及分析

2.1 升、阻力分析

笔者主要关注不同间距情况下各方柱的阻力、升力系数与变化情况，简略分析了流场演变情况。

表2给出了不同间距下上游方柱的阻力、升力与斯特劳哈数。在L/D=1时，两方柱的升力都非常的小，表明两方柱此时的脉动微弱;在L/D=2时，上游方柱阻力较其他情况时有所减小，说明间距较小时，两柱存在干扰作用。随着间距比的不断增大，上游方柱阻力(图3)与斯特劳哈数St趋于单柱绕流情况下的情形;在L/D=3时上下方柱的升力都变化较大，此种间距比下游方柱增加的升力有较大增加，主要是因为：上游方柱的尾流对下游方柱的来流有很大影响，此间距下上游方柱的尾涡已开始脱落，扩散出去，改变了下游方柱的来流(图4)，导致上下游方柱的升力都有大幅度的增加。

表2 上下游方柱阻力计算结果Table 2 Calculation results of drags of square cylinders at upstream and downstream

图3 上下游方柱阻力与升力系数走势Fig.3 Trend of drag and lift coefficient of upstream and downstream square cylinder

图4 流线图局部放大Fig.4 Local amplification of flow line

从表2可以看出，在L/D=1与2间距下时下游方柱阻力为负值，此时方柱受力为水流的相反方向，其主要原因是：当两方柱间距较小时(如L/D=1与2)，下游方柱受上游方柱尾流漩涡影响，柱前形成为负压，从而导致这样的结果，此结果与一般的实验情况基本吻合。此时两方柱的升力系数非常小，斯特劳哈数St较单柱情况时变小，说明方柱的脉动较小，而涡的形成频率较单柱时加快。随后方柱脉动开始变大，上游方柱阻力有所减小，但减小得并不十分明显，而后两方柱的脉动放缓。两方柱的间距比L/D值的变化对上游方柱所受阻力影响不大，主要为上游方柱对下游方柱的影响;当L/D≥5时，上游方柱的所受阻力、升力、斯特劳哈数均与单柱情况几乎一致。随着方柱间距的增大，下游方柱所受阻力呈变大的趋势，升力较单柱时大了近一倍左右。其原因为下游方柱位于上游方柱分离的脉动高速区附近，上游方柱脱落的涡直接作用于下游方柱，产生更小尺度的涡，在其前角产生额外的角动量，从而产生这样的结果。

当两方柱靠得较近时，阻力与升力变化都比较剧烈，其变化的趋势各不相同，当距离较远时，两方柱的阻力趋于一致，升力也趋于稳定，这在工程设计建设中对水流荷载的考虑提供一定参考价值。

2.2 流场演变

图5给出5种情形下的瞬时流线图。间距较小时，只在方柱背后产生漩涡，两方柱附近的流场改变不大，尾流区较远处没有涡的摆动;随着L的增大，下游方柱前后流态变化明显，尾流区形成周期性的涡街，两柱都有规律性涡脱落，并且下游方柱涡街摆动越来越大，说明L的增大增加了两方柱尾流的不稳定性，而上游方柱周围流场几乎不受下游方柱影响。从图中对比可以看出，串列双方柱情形下流场只有在L/D=1间距比下才出现了对称情况，并伴有对称尾流，其余情况主要为偏转尾流。在L/D=2时两柱之间有较大回流区，随着L的增大，回流区有一定的减弱。

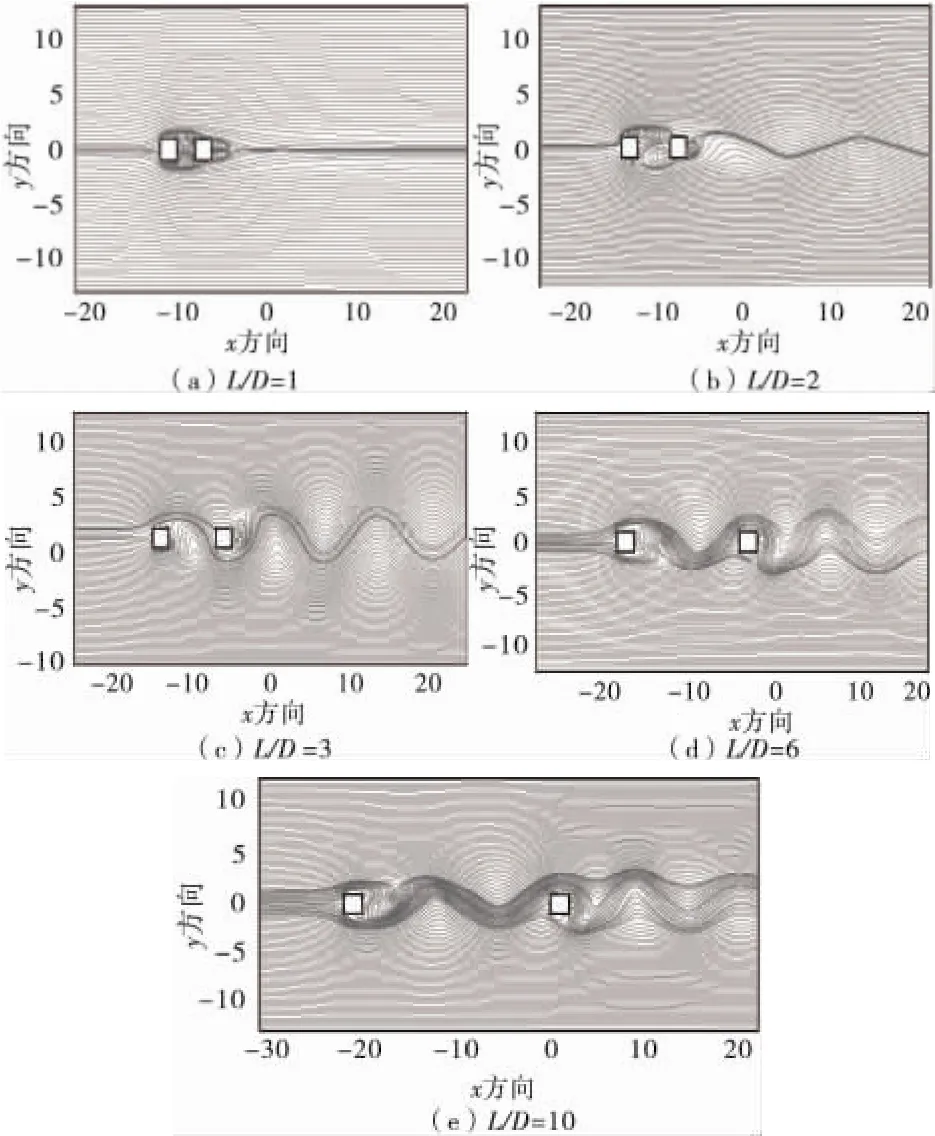
图5 流线图Fig.5 Flow line

图6给出了 L/D 为1，2，3，6，10情况下的涡量图。可以发现，随着间距的增大，涡量较大的地方由方柱两侧移向方柱的后方，而后方柱却刚好相反。

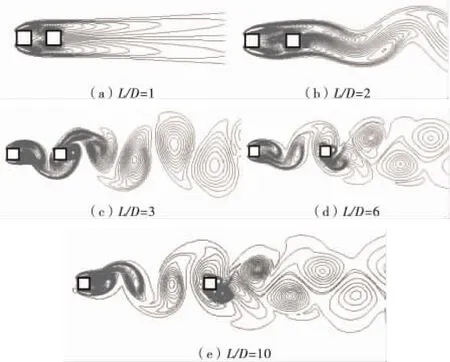
图6 涡量图Fig.6 The vorticity

3 结论

笔者主要研究了两串列方柱扰流的干扰情况。模拟计算过程中发现，两方柱间网格精度尤为重要，直接关系到下游方柱绕流特性模拟所得的数值。经研究得到以下结论：

1)当两方柱串列排列时，上游方柱所受阻力几乎无变化，与单方柱情形时大致相同。

2)下游方柱所受阻力在随着间距的增大而先减小后增大，且均小于上游方柱所受阻力，屏蔽效应明显;由于上游方柱的存在，下游方柱升力明显增大。

3)间距较大时，上下游方柱的脉动频率几乎相等。

4)在串联时两方柱之间间距L的变化对流场的改变作用明显。

［1］Lyn D A，Einav S，Rodi W.Laser doppler velocimetry study of ensemble-averaged characteristic of the turbulent flow near of a square cylinder［J］.Fluid Mechanics，1995，304：285-319.

［2］Lyn D A，Rodi W.The flapping shear layer formed by flow separation from the forward corner of a square cylinder［J］.Fluid Mesh，1994，267：353-376.

［3］Hiromasa Kawai，Kiyoshi Fujinamic.Numerical Simulation of Flow around Square Prisms in Tandem Arrangements［C］//9thICME.Houston Texas：Gulf Publishing，1995：185-186.

［4］王远成，吴文权.方柱绕流流场的RNG方法模拟研究［J］.水动力学研究与进展：A，2004，19(增刊1)：916-920.Wang Yuancheng，Wu Wenquan.Numerical simulation of flow around square cylinder using RNG k-ε turbulence model［J］.Journal Hydrodynamics：A，2004，19(S1)：916-920.

［5］Muralami S，Mochida A.3-D numerical simulation of airflow around a cubic model by means of the k-ε model［J］.Journal of Wind Engineering and Industrial Aerodynamics，1988，31(1)：327-338.

［6］陈素琴，黄自萍，沈剑华，等.两串列绕流的干扰数值模拟研究［J］.同济大学学报：自然科学版，2001，29(3)：320-325.Chen Suqin，Huang Ziping，Shen Jianhua，et al.Numerical computation of the flow around two square cylinders in tandem arrangement［J］.Journal of Tongji University：Natural Science，2001，29(3)：320-325.

［7］张远君.流体力学大全［M］.北京：北京航空航天大学出版社，1991.Zhang Yuanjun.Fluid Mechanics［M］.Beijing：Beijing University of Aeronautics and Astronautics Press，1991.

［8］Rodi W.Simulation of flow past buildings with statistical turbulence models［J］.Wind Climate in Cities，1995，277：649-668.