滑坡抗剪强度参数反演数值模拟研究
刘光华,熊 超,赵 鹏
(1.重庆交通大学岩土工程研究所,重庆400074;2.重庆市地质灾害防治工程勘查设计院,重庆400700)
滑坡是丘陵山区主要的地质灾害类型及灾害性地貌过程,具有强致灾性和毁灭性的特点。丘陵山区滑坡灾害频繁发生,往往导致交通中断、航道阻塞,严重威胁居民生命财产安全。
在进行滑坡稳定性评价及防治工程设计时,滑坡抗剪强度参数的选择十分困难,而滑坡推力对c,φ值很敏感,强度参数发生微小的变化,其滑坡推力可能成倍增加,直接影响滑坡稳定性评价及治理工程设计的合理性、安全性、经济性。目前c,φ值的确定常根据室内试验或现场试验,结合有关工程经验数值,由极限平衡原理,建立计算公式进行反演求解。目前常采用以下3种方法:①假定剩余下滑力为0,安全系数K=1,滑坡处于临界状态,根据滑面土体条件结合类似土质资料或者室内试验资料,定出其中一个指标反演另一个指标,求解强度参数;②在一次滑动中,找出两个相邻近的瞬间滑动计算断面,列出两个边界条件相同的方程式,联立求解;③根据同一断面位置,不同时间但条件相似的两次滑动瞬间计算断面建立两个反演式联立求解[1-2]。极限平衡原理是将滑体假定为刚性体,相邻条块间只传递推力,因此,根据上述3种方法进行c,φ的反演有一定的局限性。
笔者运用FLAC3D有限差分的数值方法,建立计算模型,采用自编强度折减法进行稳定性求解,根据求解数值与滑坡所处稳定状态进行比较,判断其c,φ值,并与极限平衡法反演值进行比较,研究稳定系数对c,φ值的敏感性,综合确定c,φ值,为滑坡抗剪强度参数反演提出新的方法。
1 滑坡稳定性分析的强度折减法
1.1 强度折减法的定义
根据库伦公式,土体的抗剪强度τ=σtanφ+c,由于软弱面上的c,φ值低于周围土体,易于产生应力集中,因此,当软弱面上某点或某部分的应力达到和超过其抗剪强度时,首先发生剪切破坏,该点或该部分称为滑坡源。如果软弱面的抗剪强度不断降低,则进入剪切屈服的部位也不断扩展,直到这些部位发展成为一条连贯的屈服面,形成整个滑动面[3]。将土体的强度参数c,φ分别乘以1/K(图1),并用于计算抗剪强度τ值,逐渐增加K使抗剪强度逐渐降低,直至失稳破坏。
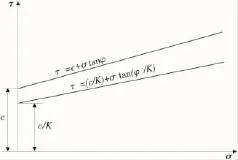
图1 抗剪强度与正应力的关系Fig.1 The relationship of normal stress and shear strength
1.2 强度折减法在FLAC3D中的实现
FLAC3D采用“二分法”[4]求解稳定系数。采用该法需定义解所在区间,合理选定区间值,可以减少计算时间。FLAC3D内置强度折减法,稳定系数的初始值分别定义为0和64,迭代计算复杂,运算时间长,不利于工程应用,因此采用自编强度折减法[5],减少计算时间。其迭代过程分下述4个步骤:
1)假定K1,K2的值,取折减系数为 Ks=(K1+K2)/2,相应的强度为 c/Ks、tanφ/Ks,进行迭代计算;
2)若单次迭代计算收敛,但|K1-K2|>ε,则K1=Ks、K2=K2带入 1)中;
3)若单次迭代计算不收敛,则K2=Ks、K1=K1带入1)中;
4)若迭代|K1-K2|<ε时,计算截止,求得稳定系数Ks=(K1+K2)/2。
经过不断的改变Ks,改变强度参数,进行循环计算,采用解的不收敛作为破坏标准,最终求得稳定系数。
1.3 稳定系数与强度参数反演的关系
所求稳定系数与滑坡体所处稳定状态相互比较,若稳定系数与滑坡体所处稳定状态相一致,则迭代计算中土体的c、φ值即为滑坡的强度参数;若所求稳定系数比滑坡体所处稳定状态偏大,则减小c,φ值后进行计算;若所求稳定系数比滑坡体所处稳定状态偏小,则增大c,φ值后进行计算。
2 工程应用
某路基填方边坡,原地形坡度较陡,在填方施工中,在路基边坡中下部设置挡土墙,坡表采用素混凝土格构护坡,但挡土墙未嵌入基岩。在暴雨作用下,表层土体呈饱水状态,大量雨水渗入坡体,使土体的重度增加,强度参数降低,土体沿土岩交界面推动挡墙发生顺坡向位移,导致后缘形成弧形裂缝,格构在土体的不均匀变形下发生断裂,且前缘挡墙未嵌入基岩,挡土墙顺滑坡体发生断裂变形,失去支撑作用。为保证该路基滑坡强度参数的准确性,对该滑坡采用有限差分强度折减法,反演其强度参数,用于滑坡推力的计算。笔者只考虑自重荷载,取该路基滑坡的强变形段进行分析,由于该路基边坡已经失稳,因此其稳定性系数取 0.95[6]。
2.1 计算模型的建立
根据郑颖人,等[7]研究认为:在均质岩土体中,坡脚到左端边界的距离为坡高的1.5倍,坡顶到右端边界的距离为坡高的2.5倍,且上下边界总高不低于2倍坡高,计算精度较为理想。但根据典型工程地质剖面图,滑坡土体为土岩组合体(图2),其坡脚为土岩交界面,因此取坡脚到左端边界的距离为10 m;由于路基边坡剖面近似为梯形,因此取坡顶到右端边界的距离为20 m;整体长度为65 m,横向宽度取10 m。在ANSYS中建立三维地质模型,划分地层单元及网格后生成符合FLAC3D的节点命令[8]。在FLAC3D生成的模型如图3。

图2 工程地质剖面Fig.2 Geological profile of engineering
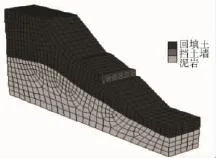
图3 滑坡有限差分模型Fig.3 FD model of landslide
2.2 材料本构模型及计算方法
岩土体的材料本构模型采用理想弹塑性模型,屈服准则采用摩尔-库伦等面积圆屈服准则。由于土体沿基岩面发生滑动失稳,取内摩擦角的变化范围为[10°,17°],步长为 1,取黏聚力的变化范围为[9 kPa,23 kPa],步长为 2,进行敏感性分析,其余物理力学参数见表1。

表1 滑坡材料参数Table 1 Material parameters of landslide
3 计算结果与分析
采用自编强度折减法对不同的c,φ值进行数值分析,稳定性计算结果如表2。采用极限平衡法计算的稳定性计算结果如表3。
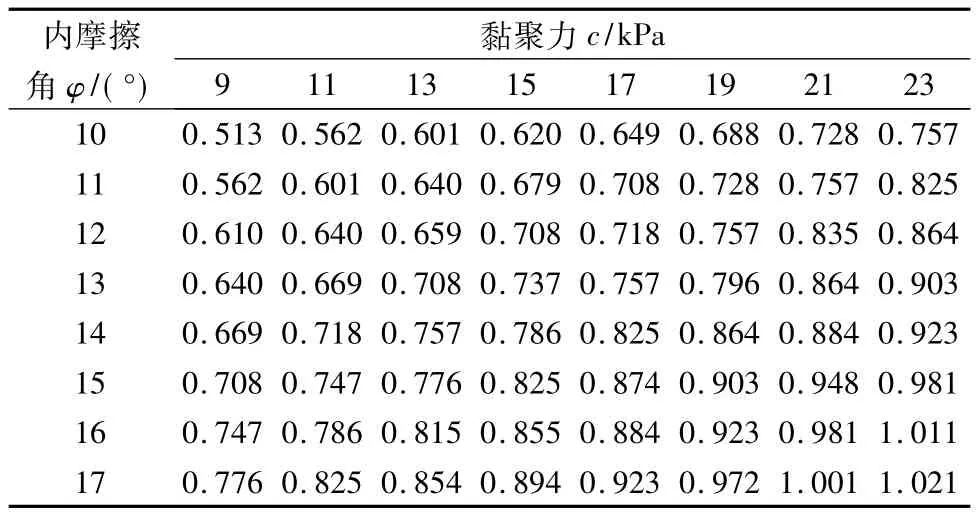
表2 FLAC3D稳定性计算结果Table 2 Stability calculation results of FLAC3D

表3 极限平衡法稳定性计算结果Table 3 Stability calculation results of LEM
对比表2、表3,极限平衡法计算的结果大于强度折减法,两种方法所求的稳定系数的相对差值总体上逐渐增大,在1.145% ~7.705%之间。由于Fs=0.95,对应于稳定性计算表,在FLAC3D稳定性计算表中相应的c=21 kPa,φ=15°,而极限平衡法稳定性计算表中c=19 kPa,φ=15°。以此为基准值进行敏感性分析。敏感性系数选用如下公式:


式中:S为敏感系数;ΔX为某因素变化量;ΔFs为Fs对应ΔX的变化量;Fso为Fs的基准值;Xmax-Xmin为某因素最大变化量。
3.1 滑坡稳定性对φ值的敏感性分析
3.1.1 强度折减法计算的Fs对φ值的敏感性分析
根据表2的稳定性系数可知,Fs-φ的关系如图4,Fs-φ 近似于线性变化,取 φ =15°,c=9 ~23 kPa进行敏感性分析,其敏感性计算结果如表4。φ对滑坡稳定性敏感系数为13.7% ~54.7%,平均值为29.6%。
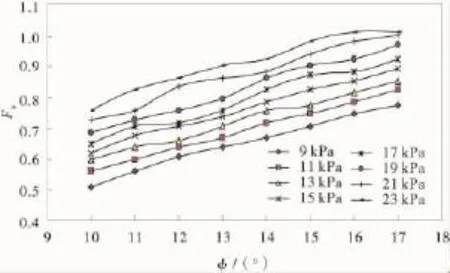
图4 Fs-φ关系曲线Fig.4 Curve of correlation between Fsand φ

表4 Fs-φ的敏感性Table 4 Sensitivity of Fs-φ
3.1.2 极限平衡法计算的Fs对φ值的敏感性分析
根据表3的稳定性系数可知,Fs-φ的关系如图5,Fs-φ 近似于线性变化,取 φ =15°,c=9 ~23 kPa进行敏感性分析,其敏感性计算结果如表5。φ对滑坡稳定性敏感系数为19.3% ~46.0%,平均值为33.4%。

图5 Fs-φ关系曲线Fig.5 Curve of correlation between Fsand φ

表5 Fs-φ的敏感性Table 5 Sensitivity of Fs-φ
3.2 c值对滑坡稳定性的敏感性分析
3.2.1 强度折减法计算的Fs对c值的敏感性分析
根据表3的稳定性系数可知,Fs-c的关系如图6,Fs-c近似于线性变化,取 c=21 kPa,φ =10°~17°进行敏感性分析,其敏感性计算结果如表6。φ对滑坡稳定性敏感系数为21.6% ~36.1%,平均值为28.8%。

图6 Fs-c关系曲线Fig.6 Curve of correlation between Fsand c

表6 Fs-c的敏感性Table 6 Sensitivity of Fs-c
3.2.2 极限平衡法计算的Fs对c值的敏感性分析
根据表4的稳定性系数可知,Fs-c的关系如图7,Fs-c近似于线性变化,取 c=19 kPa,φ =10°~17°进行敏感性分析,其敏感性计算结果如表7。φ对滑坡稳定性敏感系数为12.1% ~43.8%,平均值为26.6%。
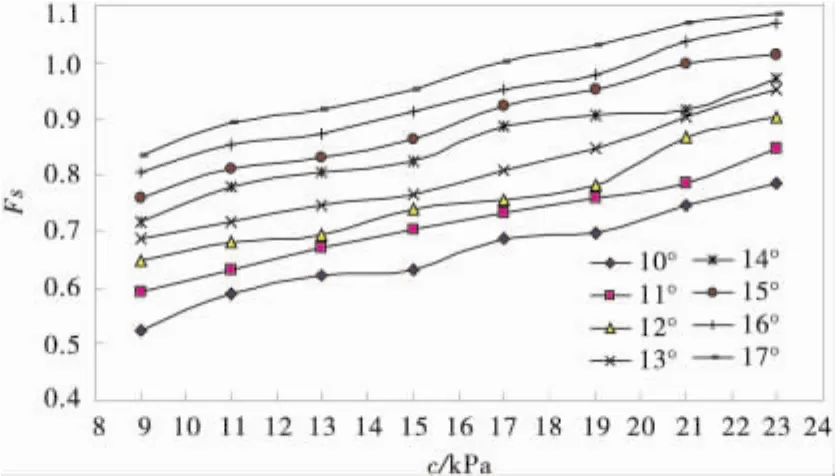
图7 Fs-c关系曲线Fig.7 Curve of correlation between Fsand c

表7 Fs-c的敏感性Table 7 Sensitivity of Fs-c
3.3 强度参数的选取
根据以上分析结果表明,φ值相对于c值对滑坡的稳定性更敏感。参数值按照FLAC3D∶极限平衡法 =1∶1 选取,因此 c=20.0 kPa,φ =15°。
3.4 数值验证
将以上分析得到的c,φ值进行数值模拟。在该值下,典型的应变增量云图如图8,在滑坡中下部其剪应变增量最大,在后缘剪应变增量相对较小,滑坡的主要破坏形式是剪切破坏,从运动形式分为牵引式滑坡。其水平位移等值线如图9,其最大位移为0.45 m,与现场实际情况基本一致,此参数可用于滑坡支挡结构设计。
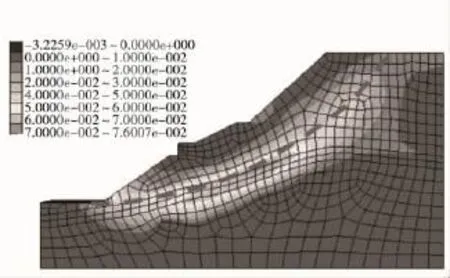
图8 剪应变增量云图Fig.8 Contour of shear-strain increment
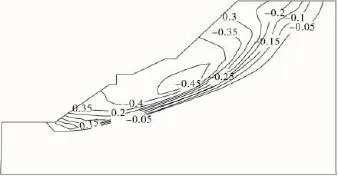
位移等值线Fig.9 Displacement equivalence value maps
3.5 对比分析
将反算后的c,φ值用传递系数法计算,滑坡的剩余下滑力为235.32 kN,稳定系数为0.971;根据滑坡土体室内快剪试验得出的岩土参数(c=19.2 kPa,φ =14.5°)计算出滑坡的剩余下滑力为 258.57 kN,稳定系数为0.962。二者值所计算的结果误差在10%以内,能达到工程治理设计的精度。因此,反演计算的结果能用于工程实践,指导工程设计。
4 结论
1)笔者基于自编强度折减法对滑坡抗剪强度参数进行反算,结果表明强度折减法计算所得的稳定系数与极限平衡法所得结果较一致,其相对误差主要是由于极限平衡法假定滑块之间为刚性体,不产生变形,数值模拟方法采用的是弹塑性材料进行岩土体的模拟,允许变形。通过强度折减法与极限平衡法的比较,按照一定比例选取c,φ值进行滑坡的治理工程设计可行。
2)强度折减法计算的稳定系数对c,φ值进行敏感性分析认为φ值相对于c值更敏感,与极限平衡法分析结果相一致。
3)在滑坡中下部剪应变增量最大,在后缘剪应变增量相对较小,滑坡的主要破坏形式是剪切破坏,从运动形式分为牵引式滑坡。
4)笔者仅仅是将一个特定的填方路基滑坡作为研究对象,通过改变c,φ值得出稳定系数,通过与极限平衡法的相互比较得出c,φ值,并通过室内试验印证了该方法能满足工程精度的要求。该方法对于其他滑坡同样适用,可供大家参考借鉴,解决工程实际问题。
[1]王松龄.滑坡区岩土工程勘察与整治[M].北京:中国铁道出版社,2001.Wang Songling.Landslide Area of Geotechnical Engineering and Renovation[M].Beijing:China Railway Publishing Press,2001.
[2]刘天韵,吕和林.滑坡土体抗剪强度指标反算研究[J].西部探矿工程,2004(3):185-187.Liu Tianyun,Lv Helin.Research on the back calculation of the landslide’s anti-sbear strength index[J].West-China Exploration Engineering,2004(3):185-187.
[3]潘家铮.建筑物的抗滑稳定和滑坡分析[M].北京:中国水利水电出版社,1980.Pan Jiazheng.Analysis of the Building Sliding Stability and Landslides[M].Beijing:China Water Power Press,1980.
[4]颜庆津.数值分析[M].北京:北京航空航天大学出版社,2006.Yan Qingjin.Numerical Analysis[M].Beijing:Beihang University Press,2006.
[5]陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京:中国水利水电出版社,2009.Chen Yumin,Xu Dingping.Basis and Engineering Application of FLAC/FLAC3D[M].Beijing:China Water Power Press,2009.
[6]DZ/T 0219—2006滑坡防治工程设计与施工技术规范地质矿产行业标准[S].北京:中国标准出版社,2006.DZ/T 0219—2006 Specification of Design and Construction for Landslide Stabilization[S].Beijing:China Planning Press,2006.
[7]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.Zheng Yingren,Zhao Shangyi.Application of strength reduction fem in soil and rock slope[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(19):3381-3388.
[8]廖秋林,曾钱帮,刘彤,等.基于 ANSYS平台复杂地质体FLAC3D模型的自动生成[J].岩石力学与工程学报,2005,24(6):1010-1013.Liao Qiulin,Zeng Qianbang,Liu Tong,et al.Automatic model generation of complex geologic body with FLAC3D based on ANSYS platform[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(6):1010-1013.

