参数化诱导槽设计的吸能盒结构抗撞性多目标优化
郝 亮,徐 涛,2,崔 健,吉野辰萌
(1.吉林大学 机械科学与工程学院,长春 130022;2.吉林大学 汽车仿真与控制国家重点实验室,长春 130022)
为保证车辆正面碰撞时对吸能盒在吸能的同时尽量降低最大压溃力,应对其壁厚、截面形状、尺寸等参数进行科学设计及优化,得到符合抗撞性需求的设计方案。Alexander[1]最先提出能够预测金属圆管轴向渐进叠缩变形吸能的理论模型,为薄壁结构耐撞性研究奠定了理论基础。Lanzi等[2]针对锥形吸能结构在不同工况下的变形效果,采用径向基法和遗传算法对该结构的抗撞性能进行了优化,提出符合吸能效果且满足轻量化的吸能结构;Nagel等[3]对矩形截面的锥管在动载下的吸能性进行了分析,得出如壁厚、角度等几何参数对结构吸能性的影响,并且证明了矩形截面锥管的吸能效果;Liu[4-5]研究了矩形截面薄壁梁、正六边形截面薄壁梁、槽型薄壁梁的简化模型,并建立一种用梁单元和弹簧单元来模拟薄壁梁轴向压溃的简化模型。Hosseinipour等[6]针对薄壁圆柱管施加矩形诱导槽,证明了科学地加入诱导槽可对结构的变形起到稳定作用,并可控制结构的力-位移曲线效果及吸能特性;Elgalai等[7]研究了带有波纹诱导结构的圆柱管在轴向压溃下的变形效果,认为影响该结构吸能特性的最大因素是波纹诱导结构的角度;李邦国等[8]在矩形截面薄壁管吸能部件的两侧壁上构造凹槽,使结构在吸能的同时可以提供较为平稳的轴向反力,并具有良好的变形模式。
然而,多数研究或者是针对圆形截面吸能结构,或者是采取一致等分均匀施加诱导槽的形式进行的。事实上,矩形截面吸能盒结构在工程实际中广泛存在,且易于加工。文献[3]也证明了矩形截面锥管吸能效果良好。如何科学地引入诱导槽,如槽的个数、形状,以及是否均匀分布、排布位置设计等,都将直接影响吸能盒结构的抗撞性。本文从工程实际出发,对方形截面吸能盒结构引入非均匀动态参数化诱导槽,兼顾考虑吸能、峰值压溃力及质量这三个因素,构造一种多目标优化设计方案。
1 模型建立及碰撞评价描述
常见的无诱导槽方形截面薄壁锥管的几何模型及尺寸参数如图1所示。材料属性采用低碳钢的属性标准,材料泊松比、密度和杨氏模量分别为0.3、7850kg/m3和210GPa。通过 HYPERMESH软件,采用四节点壳单元和少部分的三角形单元来建立此结构的有限元模型。四边形单元长度为5 mm,局部网格加密后不小于2mm。随后,基于显式、非线性有限元求解器LS-DYNA进行有限元碰撞仿真。对结构底端固定,并采用初始速度为5 m/s、轴向质量为500kg的刚性墙进行撞击(见图1)。薄壁锥管结构的自身接触以及其与刚性墙之间的接触均采用自动单面接触算法;静力学和动力学摩擦因数分别为0.3和0.2;与移动刚性墙之间的摩擦因数为0.3。
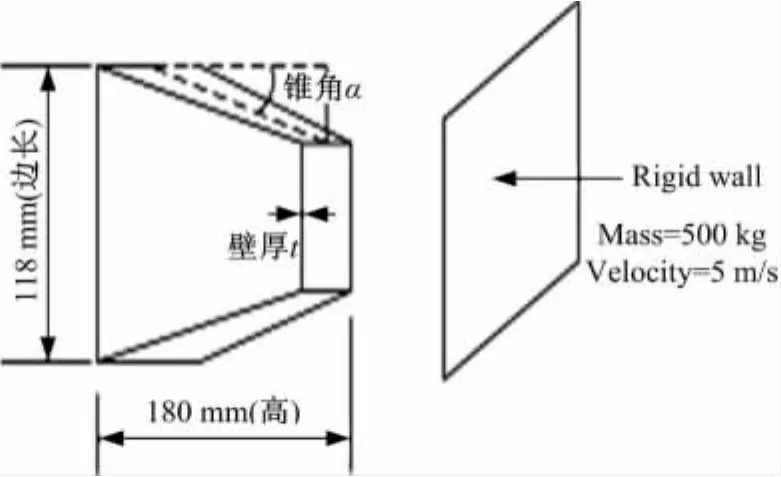
图1 刚性墙撞击锥管示意图Fig.1 Taper tube impacted with a rigid wall
在碰撞过程中,通常把降低峰值压溃力和增加能量吸收作为衡量吸能装置效率的主要标准。此外,质量也是衡量结构抗撞性能的重要因素。本文将压溃力效率(CFE)和比吸能(SEA)[9]作为评价吸能盒结构抗撞性的主要标准。CFE为平均压溃力与峰值压溃力的比值;SEA为吸能值与质量的比值[10],这样便可综合考虑能量吸收与重量效率。
由于结构强度较小时峰值压溃力相对也较小,而结构吸能性在一定范围内是随着结构强度的增加而增大。因此,对结构施加诱导槽后虽然会显著降低峰值压溃力,但由于诱导槽的引入会使整体结构质量略有增加,从而影响结构的吸能效果。因此如何协调这相对矛盾的评价指标,对提高吸能盒结构抗撞性具有重要意义。为综合考虑设计变量变化对CFE和SEA的影响,本文提出将评价指标定义为CFE和SEA的加权组合形式W,即
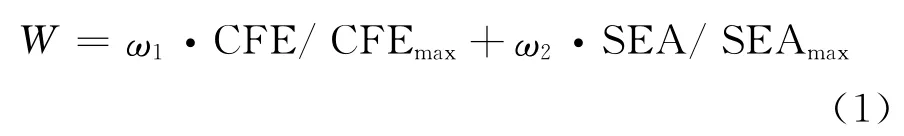
并寻求W 的最大值。至此,建立了以CFE和SEA取最大值的多目标优化问题。式(1)中ω1+ω2=1(ω1,ω2>0)是用以人为平衡CFE和SEA重要程度的权因子(通常可取ω1=ω2=0.5)。为使两者量级统一,式(1)中CFE/CFEmax和SEA/SEAmax分别是CFE和SEA的归一化变量形式。
针对提出的模型评价指标,提出了优化设计方案:首先通过正交试验筛选出初始无诱导槽的最优结构;再根据初始优化结构,实现对带有诱导槽结构的多目标优化。
2 DOE筛选无诱导槽方形截面薄壁的初始结构
本文基于正交试验设计[11],以锥角α∈ [1°,10°]和壁厚t∈ [1,2.5]mm作为试验因素。选取10水平正交表L100(1011),共需100次试验,通过LS-DYNA软件计算CFE和SEA。
根据100次正交试验数据进行3次多项式响应面拟合,得到无凹槽结构关于评价指标CFE、SEA以及W 的代理模型,如图2和图3所示,图中黑色点表示样本点。现通过分析代理模型图来研究各设计变量变化对评价指标的影响:在锥角α不变的情况下,随着壁厚t增加,CFE增加,而SEA先增大后减小,W 增大;当壁厚t相同时,随着锥角α增大,CFE、SEA及W 均增加。在100次试验中CFE和SEA的最大值分别是CFEmax=0.513和SEAmax=8099.092,见表1。W 最大值为0.816,此时对应的参数为:锥角α=10°,壁厚t=2.17mm。取此组设计参数建立无诱导槽结构模型,作为下一步引入诱导槽之后优化设计的初始结构。

图2 CFE和SEA的代理模型Fig.2 Surrogate models of CFE and SEA
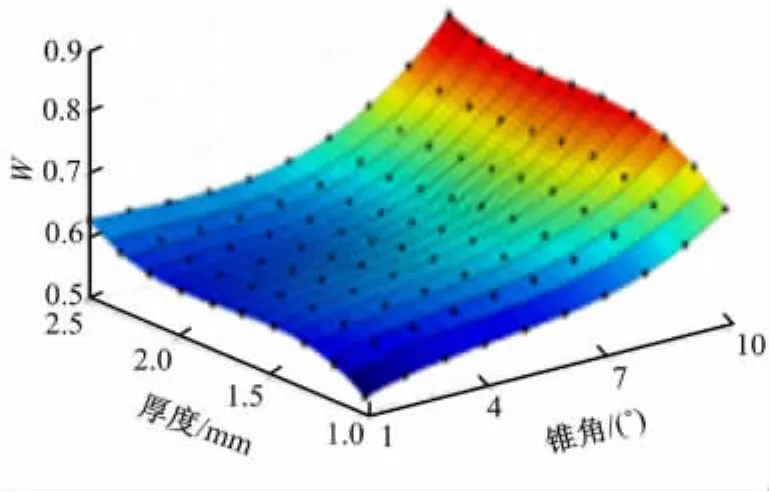
图3 W的代理模型Fig.3 Surrogate model of W
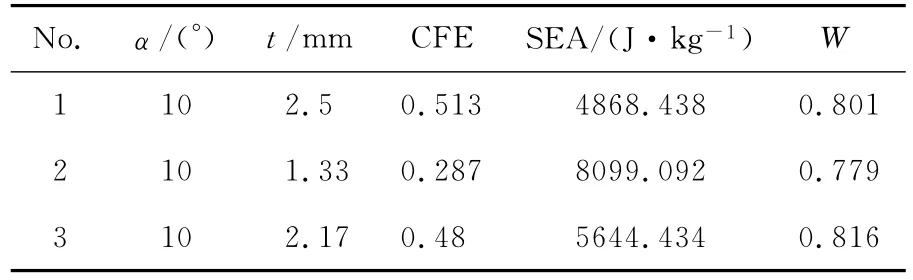
表1 无诱导槽结构最优参数Table 1 Optimal parameters of structure without inducing groove
3 引入诱导槽的方形截面薄壁结构多目标优化
基于上述优化结果,本文取锥角α=10°、壁厚t=2.17mm的无诱导槽锥管结构,研究引入诱导槽对结构抗撞性能的影响。
诱导槽可行域设定方式如下:分别在整个初始结构以及该结构前段50%部分均匀施加4个垂直高度为5mm的矩形诱导槽(见图4)。随后,在相同工况下对这两个模型进行有限元仿真(见表2)。图4(b)相对图4(a)而言,结构不仅轻量化,同时还有更高的CFE、SEA及W 值。这是因为上部施加诱导槽可有效减小最大压溃力,而下部无槽结构相对强度较大,可增加吸能值并减小整体结构质量。因此,本文将布置诱导槽的可行域确定为该结构的上半部分。

图4 4诱导槽结构示意图Fig.4 Structure with 4inducing grooves

表2 两种施加诱导槽方式的有限元仿真结果Table 2 FE simulation results of structures with inducing grooves by two ways
3.1 选取样本点
现对壁厚t=2.17mm、角度α=10°的无诱导槽结构前50%部分分别施加1、2、3个诱导槽,见图5。记诱导槽个数为N,深度为d(以槽下端深入距离为准),高度固定为5mm,h1、h2、h3为诱导槽间距,均为动态设计变量,具体见图5。此时针对以上3种施加方式分别选择具有不同诱导槽间距和深度的代表性的样本点(N=1时为15个样本点;N=2时为18个样本点,N=3时为39个样本点),见表3。
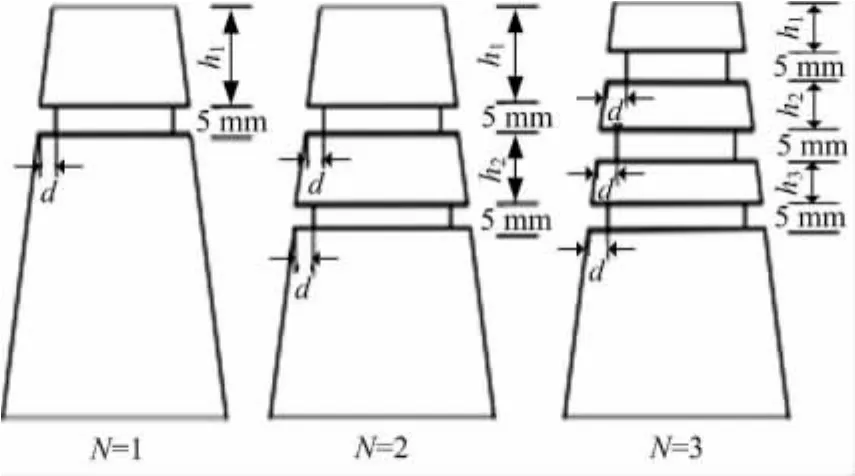
图5 带诱导槽结构示意图Fig.5 Structure with inducing grooves
3.2 构建代理模型
由于本文研究的抗撞性优化问题是高度非线性问题,因此需要根据3.1节中给出的带诱导槽结构的样本点集,构建原结构有效的代理模型。代理模型是用较为简单的函数关系近似替代实际的复杂仿真模型,可以方便地进行分析计算和优化设计,有效节省工作量和计算成本。本文采用三次多项式响应面法和径向基法[12]分别构建具有1、2、3个诱导槽的代理模型CFE′和SEA′。随后,通过计算相关系数R∈[0,1][12]检验两种方法建立的代理模型的精度。R越接近1意味着代理模型与原模型拟合效果越好。如代理模型的拟合效果不能达到要求,则需重新选取试验点构建代理模型,直到拟合效果达到要求为止。由表4可见,当N=2和N=3时,采用径向基法构建代理模型CFE′和SEA′精度较高;而当N=1时,采用三次多项式响应面法构建代理模型CFE′,径向基法构建代理模型SEA′效果较好。根据代理模型CFE′和SEA′,改写式(1)中W 为
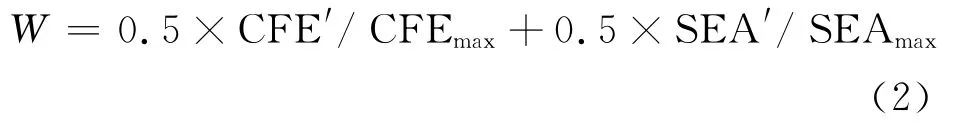
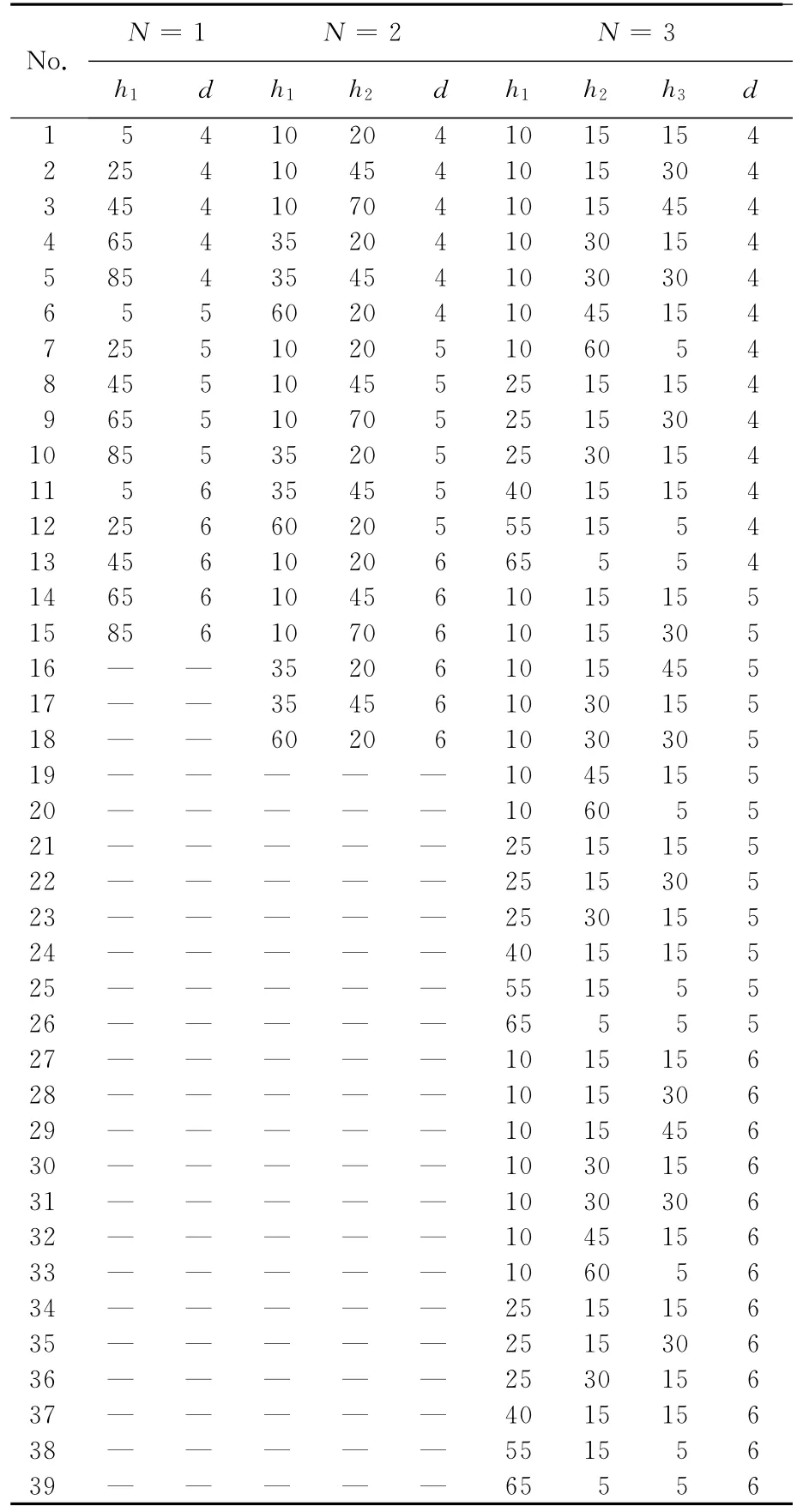
表3 具有3个诱导槽结构样本点Table 3 Sample points of structure with 3inducing grooves

表4 代理模型精度Table 4 Accuracy of surrogate models
3.3 优化设计
现采用粒子群优化(Particle swarm optimization,PSO)算法[13]分别对本文构建的带有1、2、3个诱导槽结构的代理模型进行优化设计。给定PSO算法的种群数T=40,迭代次数kmax=100,计算多目标优化问题数学模型
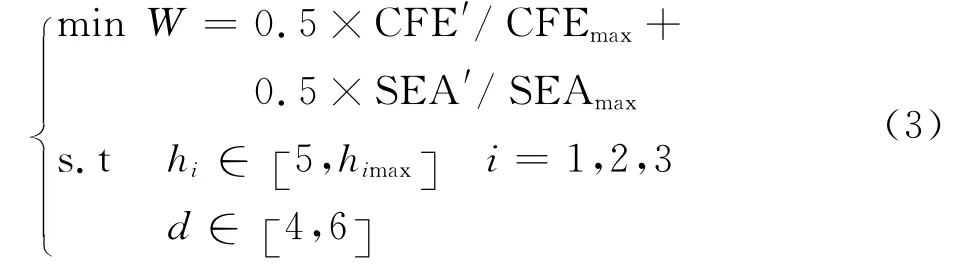
hi的上限himax根据具体情况计算。通过20次迭代便已收敛到最优值,此时分别得到诱导槽个数为1、2、3时的最优设计参数(见表5)。为验证参数的有效性,将表5中相应参数带入其有限元模型中进行计算,见表6中各模型的结果。

表5 三种施加诱导槽情况下的最优设计参数Table 5 Optimal parameters among three methods of inducing grooves

表6 带诱导槽结构与无诱导槽结构最优结果比较Table 6 Comparison of optimal results between structure with inducing grooves and one without inducing groove
3种带诱导槽结构的CFE值均优于无诱导槽结构,分别提高约35%、58%和58%,其中CFE提高最明显的情况出现在诱导槽个数为1时(0.76)。而比较SEA值可知,由于施加诱导槽造成结构质量增加,导致SEA值分别降低3%、5%和9%。此外,3种带诱导槽结构的W 值分别比无诱导槽结构提高了约18.4%、31.3%和28.9%,最优值(1.071)出现在施加2个诱导槽的情况,此时SEA值相对于无诱导槽结构仅减小5%,与大幅提高的CFE值相比,很好地达到了提高抗撞性的作用。
图6为无诱导槽结构和施加2个诱导槽结构的压溃变形图,可见施加了诱导槽的结构变形更规则、稳定、易控。

图6 无诱导槽和带有2个诱导槽结构压溃变形图Fig.6 Collapse of structures without inducing groove and with two inducing grooves
值得说明的是,由于方形截面与圆形截面是工程实际中车身吸能盒结构的两种常见截面形状,为进一步验证本文优化设计的方形截面吸能盒结构的抗撞性能,现基于表6中已优化出的带有2个诱导槽的方形截面锥管最优设计参数,构建相应的圆形截面锥管结构,其参数设置参照图1,其中结构高度为180mm,锥角α=10°,厚度t=2.17mm,将原方形截面的底边边长(115mm)作为圆形截面底边的直径。按表5中带诱导槽的方形截面最优参数,即施加2个诱导槽(h1=60 mm,h2=27.235mm,d=4mm),构建圆形截面锥管结构有限元模型,如图7所示。
图7 带有2个诱导槽的圆形截面锥管结构有限元模型Fig.7 FE model of circular cross section taper tube with two inducing grooves
表7为与此组参数对应的有限元计算结果。可见,与圆形截面锥管结构相比,带有诱导槽的方形截面锥管结构的CFE值提高了38.9%,虽然SEA略微下降了5.3%,但W值提高了23%。因此,综合分析以上结果可知:带诱导槽的方形截面锥管结构的抗撞性能要优于同等参数下构建的圆形截面结构。
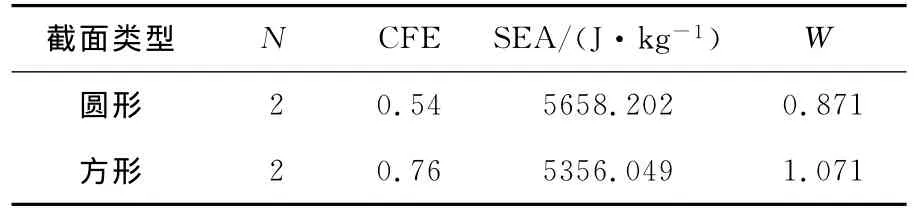
表7 带诱导槽的圆形与方形截面锥管结构抗撞性能对比Table 7 Comparison of crashworthiness of circular and square cross section taper tubes with inducing grooves
4 结束语
探讨了如何在低速正碰工况下,提高汽车前部抗撞性部件——吸能盒结构抗撞性能的有效方法。将CFE和SEA两者的加权组合形式作为评价指标,建立同时兼顾降低压溃力、提高比吸能的多目标优化模型,科学分析设定施加诱导槽的可行区域,参数化动态布置诱导槽的优化方案。基于DOE筛选的无槽初始结构作为优化的良好种子,有效建立非线性代理模型,为PSO算法对代理模型优化设计奠定了基础。优化计算获得方形截面锥管结构最优的诱导槽数量、深度及位置,确定施加诱导槽的最优方案。计算分析结构,表明此方法的科学有效性。总之,对本文采用方形截面锥管结构来模拟吸能盒的研究中,通过科学引入诱导槽的设计,会在保证比吸能基本稳定的情况下,大大降低车辆在发生正面碰撞时的峰值压溃力。此方法可为吸能装置结构的科学设计提供思路。
[1]Alexander J M.An approximate analysis of the collapse of thin cylindrical shells under axial loading[J].Quarterly Journal of Mechanics and Applied Mathematics,1960,13(1):10-15.
[2]Lanzi L,Castelletti L M L,Anghileri M.Multiobjective optimization of composite absorber shape under crashworthiness requirements[J].Composite Structures,2004,65(3-4):433-441.
[3]Nagel G M,Thambiratnam D P.Dynamic simulation and energy absorption of tapered thin-walled tubes under oblique impact loading[J].International Journal of Impact Engineering,2006,32(10):1595-1620.
[4]Liu Y C.Crashworthiness design of multi-corner thin-walled columns[J].Thin-walled Structures,2008,46(12):1329-1337.
[5]Liu Y C.Crashworthiness design of thin-walled curved beams with box and channel cross sections[J].International Journal of Crashworthiness,2010,15(4):413-423.
[6]Hosseinipour S J,Daneshi G H.Energy absorbtion and mean crushing load of thin-walled grooved tubes under axial compression[J].Thin-walled Structures,2003,41(1):31-46.
[7]Elgalai A M,Mahdi E,Hamouda A M S,et al.Crushing response of composite corrugated tubes to quasi-static axial loading[J].Composite Structures,2004,66(1-4):665-671.
[8]李邦国,陈潇凯,林逸.车用吸能部件吸能特性的改进[J].吉林大学学报:工学版,2009,39(1):12-16.Li Bang-guo,Chen Xiao-kai,Lin Yi.Capacity enhancement of impact energy-absorbing member of vehicle[J].Journal of Jilin University(Engineering and Technology Edition),2009,39(1):12-16.
[9]Jin S Y,Altenhof W.Comparison of the load/displacement and energy absorption performance of round and square AA6061-T6extrusions under a cutting deformation mode[J].International Journal of Crashworthiness,2007,12(3):265-278.
[10]Liu Y.Design optimization of tapered thin-walled square tubes[J].International Journal of Crashworthiness,2008,13(5):543-550.
[11]Simpson T W,Lin D K J,Chen W.Sampling strategies for computer experiments:design and analysis[J].International Journal of Reliability and Applications,2001,2(3):209-240.
[12]Jin R,Chen W,Simpson T W.Comparative studies of metamodelling techniques under multiple modelling criteria[J].Structural and Multidisciplinary Optimization,2001,23:1-13.
[13]Kennedy J,Eberhart R.Particle swarm optimization[C]∥IEEE Int Conf on Neural Networks,1995:1942-1948.

