基于遗传基因理论的汽车维护生产系统优化仿真

张立斌，韩 玲，刘义才，葛淑斌，李 昱

（1.吉林大学 交通学院，长春 130022；2.中国人民解放军65316部队 装备部轮式车辆科，长春 130000；3.上海大众汽车有限公司 整车分部，上海 201805；4.中国人民解放军徐州空军学院 航空兵军交运输指挥系，江苏 徐州 221000）

我国运输车辆执行的是“定期检查、强制维护、视情修理”的汽车维修制度，汽车二级维护是其中核心内容［1］。车辆技术状况下降，不安全隐患增多，所以必须加强二级维护管理。国内汽车检测线标准不一，目前虽然已有相关生产线的研究内容，但多数只是阐述二级维护作业的违规操作［2-4］。这些研究仅是对汽车维护人员职业道德的一种行为规范，并没有涉及生产线调度的理论研究。针对上述问题，本文提出了一种基于遗传基因理论优化汽车二级维护生产线调度平衡的方法，并在汽车生产线调度问题上进行初步试验，试验结果证明该调度方法使二级维护生产线的效率得到显著提高。

1 生产线建模

汽车维护任务就是合理安排汽车生产线的车间调度，提高生产率，使维护车辆数最多。二级维护基本项目有作业11项，共48个步骤。对于生产线上每个工位的作业时间，本文取其平均值，所得作业时间更为精确化。生产线各工位的作业时间安排如图1所示。

由图1可看出，整辆车检完需183min。第2工位维护时间较长，其前设立暂存区。第4、5工位维护作业时间较短，平衡优化时可考虑合并，其后设立暂存区。第7工位维护作业时间最长，是整条生产线的“瓶颈”，在其前设立暂存区。

为了对二级维护生产线进行优化，需要对该生产线系统建立数学模型，然后通过计算机进行仿真。生产线系统建模的原则如下［5-6］：本系统模型包括1条主线、1个发生器（source）、11个处理器（processor）、4个暂存区（queue）和1个吸收器（sink）。根据以上模型实体与生产线工位对应关系建立仿真模型。仿真流程模型如图2所示，实体模型对象间的黑色线条表示各对象间已经连接。

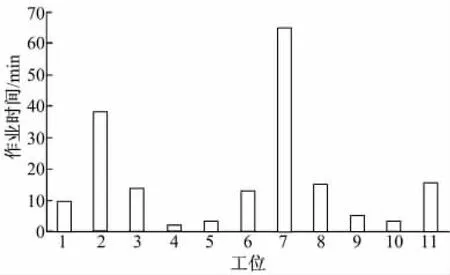
图1 各工位时间表Fig.1 Time table of work stations

由图2可看出，生产线运行混乱，工序堆积严重，各工位作业量差别较大，因此有进一步提升的空间。

从表1可知，除第7工位空闲率较低外其余各工位的空闲率过高，工位没能完全充分利用。

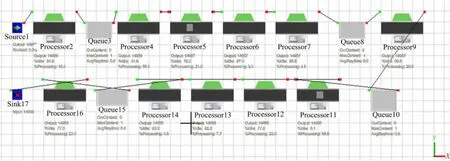
图2 二级维护生产仿真流程模型Fig.2 Vehicle maintenance simulation model

2 遗传基因预处理

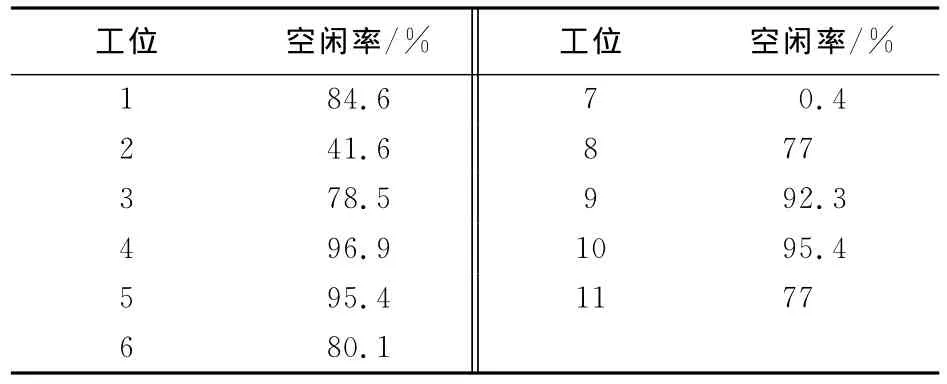
表1 各工位空闲率Table 1 Idle time ratio of work stations

2.1 工位模型精简

为更好地发挥遗传基因理论的作用，需要对待检汽车的工位进行化简。首先根据每天需维护的车辆数计算该二级生产线的节拍，把待检元素利用平衡理论和启发式算法进行平衡安排［7］。该生产线计划待检汽车为16辆，工作制为8h，节拍为：8×60÷16＝30min。

第11工位内容即全车润滑，均可在各个工位上进行，安排一名工人随车作业。第4、5工位的工时较短，将它们作为工作元素安排。第7工位由于工时较长，安排两名工人维护。平衡后工位缩减到5项，工人减少至6名。

2.2 精简后的仿真验证

生产线工位进行平衡后［8］，各工位时间如图3所示。

图4为Flexsim软件仿真平衡后的工作过程，对比图2可知，各工位运行有序。

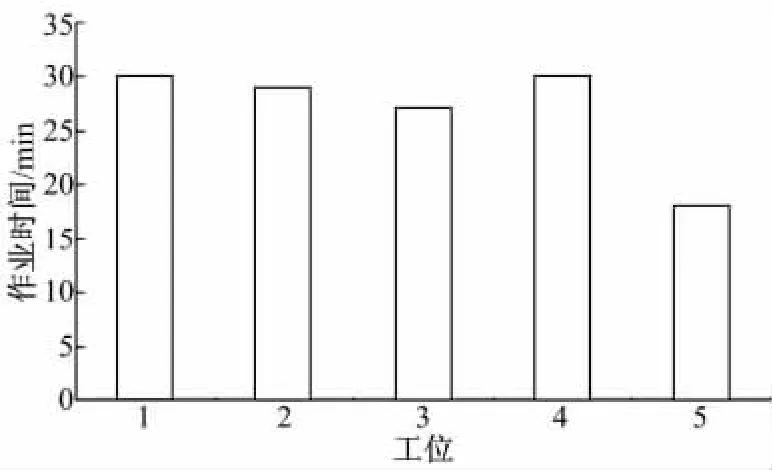
图3 平衡后各工位时间表Fig.3 Time table of work stations after balance

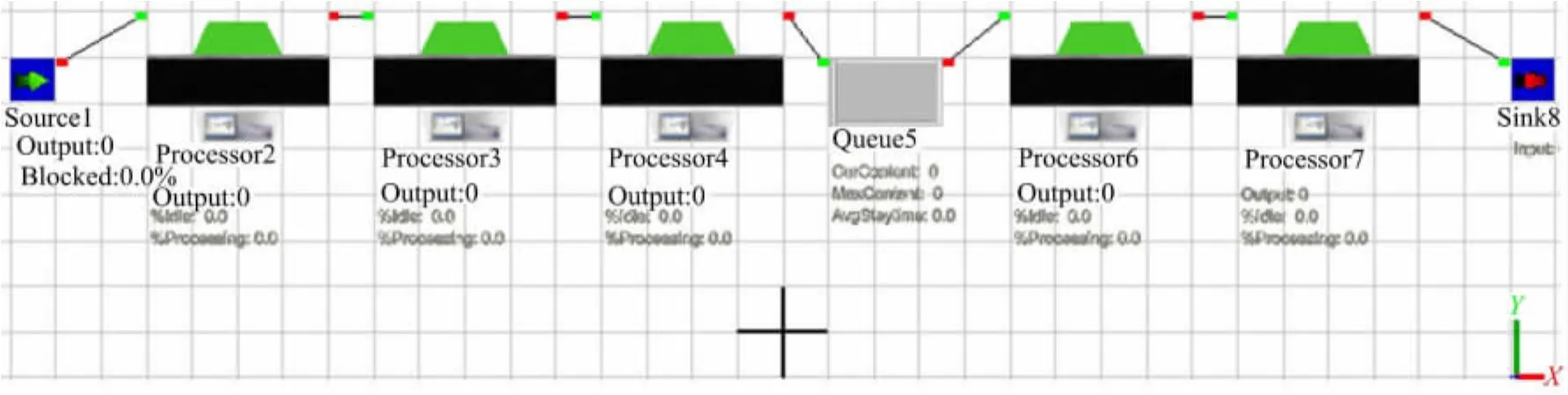
图4 Flexsim仿真平衡后的工作过程Fig.4 Working process of Flexsim simulation after balance

表2为平衡后各工位空闲率，工位平衡后空闲率大幅度减少，生产效率得到提高。

表2 平衡后各工位空闲率Table 2 Idle time ratio of work stations after balance

3 遗传基因理论应用

3.1 生产线车间调度描述

由于遗传算法不能直接处理生产调度问题的参数，所以必须通过编码将它们表示成遗传空间中由基因按一定结构组成的染色体［9-11］。如果是对6个工件进行生产调度，它们的加工顺序是j2、j4、j1、j5、j3、j6则它的编 码为：Vi＝ ［241536］。

本文生产线共有待检汽车5辆，则基因串长度为5。随机选定等待检测的5辆汽车的维护内容和维护时间不一样，所以这里的维护时间和简单启发式算法中待检汽车的维护时间有所不同。将车间调度描述为5辆待检汽车在5个工位上的流水车间调度问题，其中n为待检汽车数量（n＝5），m为工位数量（m ＝5）。

令c（ji，k）表示ji在工位k上的加工完成时间，｛j1，j2，…，jn｝表示待检汽车的调度，那么n辆待检汽车、m个工位的流水车间调度问题的完工时间可表示为

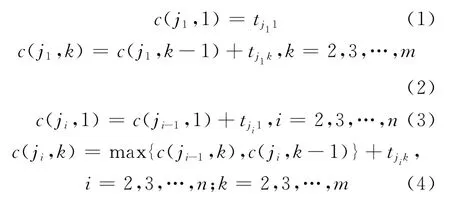
最大流程时间为

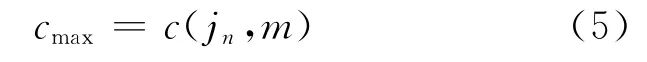
调度目标就是确定｛j1，j2，…，jn｝，使得cmax最小。算法的具体调度信息如表3所示。

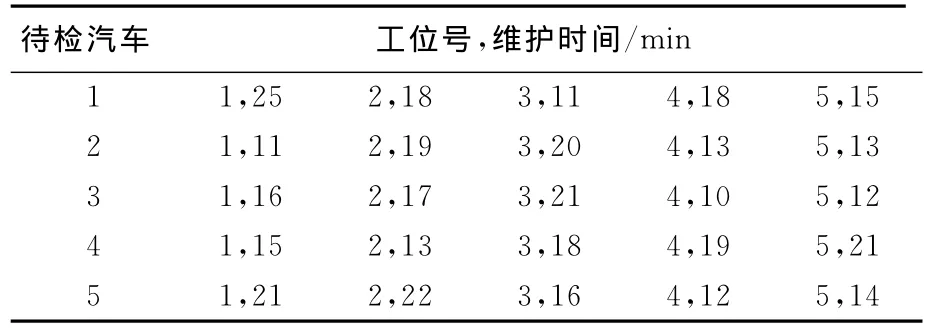
表35 ×5调度问题信息Table 35 ×5scheduling information

确定本文算法参数如下：初始群体规模为50，交叉概率为0.7，变异概率为0.006，交叉次数、变异次数、迭代次数分别为50、50、30。

通过遗传算法计算得到最优染色体为［42531］，对应该染色体的目标值为141min，即5辆汽车检验完的时间为141min，甘特图如5所示，Mi（i＝1，2，…，5）表示i工位。

5辆待检汽车分别用1、2、3、4、5代表，通过遗传算法中的选择、交叉、变异操作得到的最优染色体过程如图6所示。

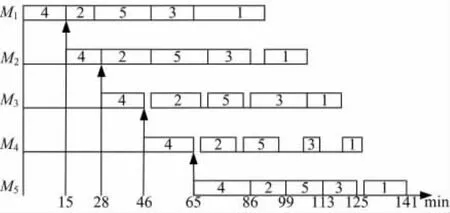
图5 最优染色体甘特图Fig.5 Optimal chromosome of Gantt

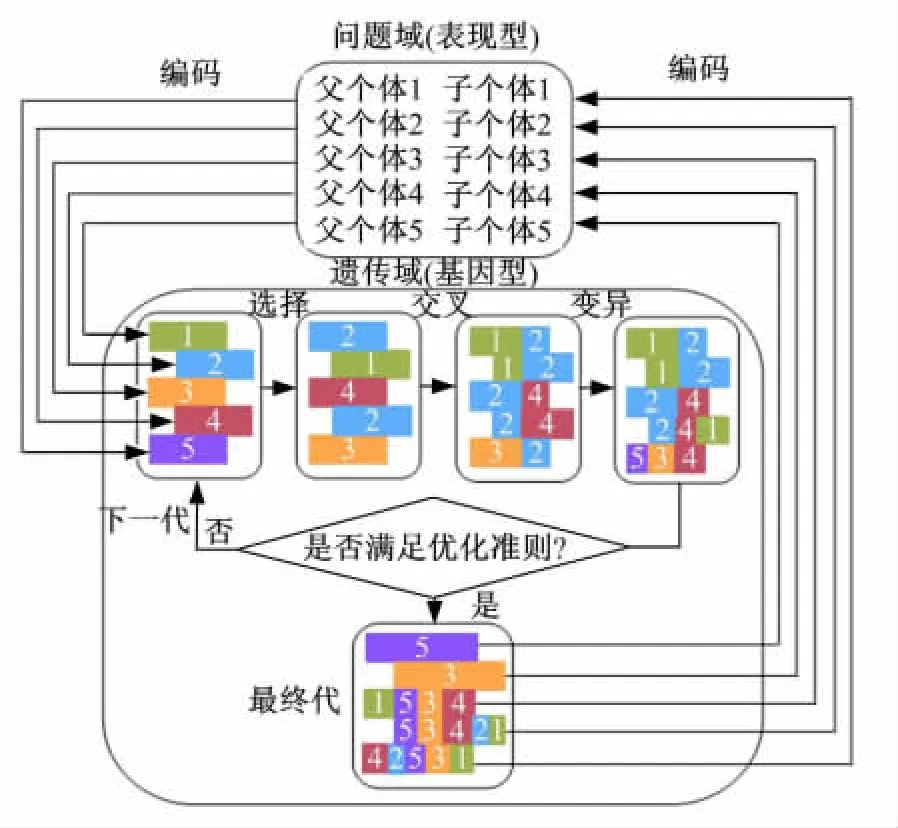
图6 基本遗传算法过程图Fig.6 Genetic algorithm process diagram

在以上5辆待选汽车选择、交叉、变异操作时除最优染色体［42531］外任选一条染色体［53124］，进行优化后的时间对比，则该染色体［53124］的目标值为183min，得到的甘特图如图7所示。

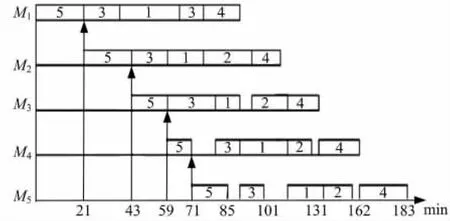
图7 非最优染色体甘特图Fig.7 Non－optimal chromosome of Gantt

综上可知：应用遗传算法计算所得到的染色体为最优。

3.2 仿真结果分析及车间动态调度验证

仿真结果表明染色体［42531］的调度结果显示为141min。因为设置暂存区的容量为5个，所以当5辆待检汽车全部维护完毕后，暂存区的车辆数目是5个。该例子中是对5辆待检汽车A1、A2、A3、A4、A5进行维护，它们历经各个工位的维护作业后，驶离生产线。若这5辆车还没有全部维护完毕时，生产线外又到达n辆待检汽车B1、B2、…、Bn，则就对这n辆进行排序。假设顺序为［23 n …1］。此时若在第一工位进行维护的是5辆待检汽车中的A1时，则把它排在n＋1辆待检汽车的第一位，利用以上算法重新排列待检汽车的作业顺序，然后按顺序进行维护作业。这样即可使整个生产线处于均衡满负荷工作状态。如图8所示，在整个二级维护生产线上，车辆的调度是一个动态过程。在维护的过程中，如果有维护任务追加或撤销等情况时，只需要重新根据以上算法进行调度规划，重新排列待检车辆的维护顺序即可。

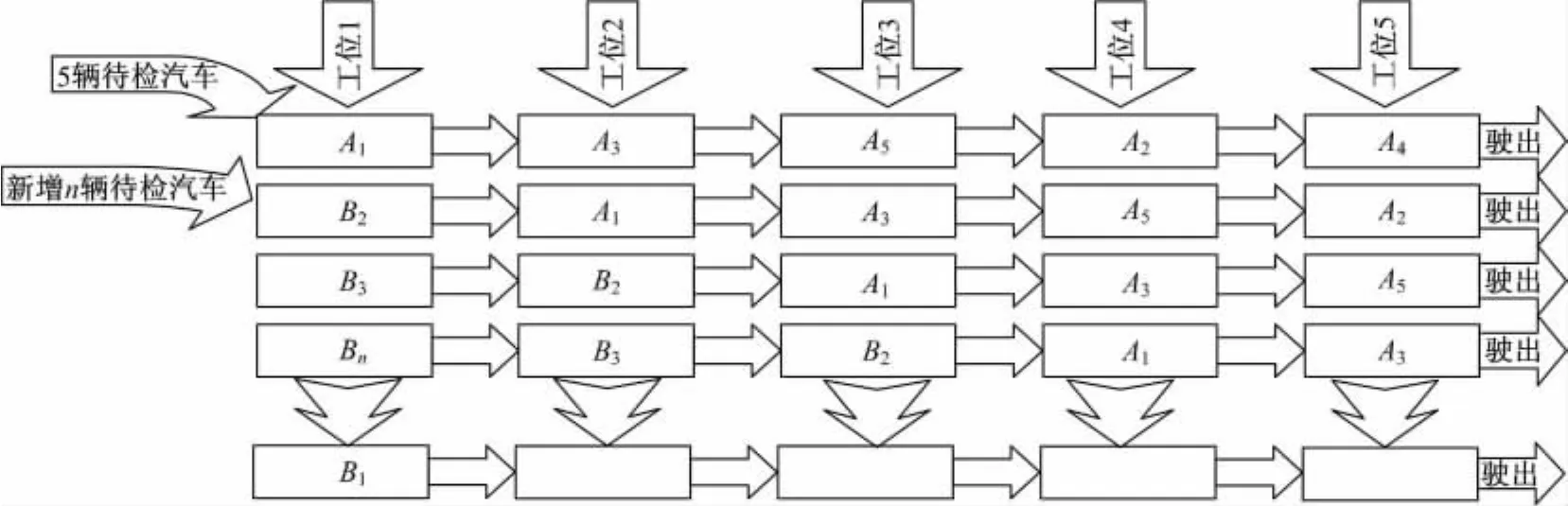
图8 5个工位的待检汽车维护作业Fig.8 Car maintenance of five work stations

4 结束语

利用Flexsim仿真软件分析了生产线的不平衡，平衡前生产线整车检验完毕需要183min。基于遗传基因理论在汽车二级维护生产线上平衡优化后，整车检完需141min，提高了生产效率。充分证明了遗传基因理论在生产线上应用的合理性、高效性。另外这种方法可以用在各种调度领域，从而提高工作效率。

［1］顾国瑞.汽车诊断技术的应用与发展［J］.云南交通科技，2001，16（1）：1－3.Gu Guo－rui.Apllication and development of automobile detection technology［J］.Yunan Communication Science and Technology，2001，16（1）：1－3.

［2］卢荣生.浅谈加强汽车二级维护和确定二级维护周期［J］.辽宁交通科技，1995（2）：38－40.Lu Rong－sheng.On the strengthening of two maintenance and vehicle maintenance cycle to determine the two［J］.Liaoning Communication Technology，1995（2）：38－40.

［3］张立斌，单洪颖，苏建.汽车检测线质量认证评价体系［J］.吉林大学学报：工学版2009，39（增刊2）：225－228.Zhang Li－bin，Shan Hong－ying，Su Jian.Vehicle inspection quality evaluation system［J］.Journal of Jilin University Engineering Science，2009，39（Sup.2）：225－228.

［4］李赞明.工业工程在生产实践中的应用［J］.机械工程，1997（5）：38－40.Li Zan－ming.The practice of industrial engineering applications in the production［J］.Industrial Engineering，1997（5）：38－40.

［5］李暄.基于Flexsim仿真软件的配送中心系统优化设计［J］.物流技术，2009（8）：66－68.Li Xuan.Flexsim simulation software based on the distribution center system optimization［J］.Logistics Technology，2009（8）：66－68.

［6］席忠民.应用工业工程优化总装作业系统［J］.材料与工艺，2000（9）：47－49／63.Xi Zhong－min.Application of industrial engineering to optimize the operating system assembly［J］.Material and Process，2000（9）47－49／63.

［7］徐华，于勇.一种实用的启发式资源平衡优化算法的改进［J］.哈尔滨商业大学学报：自然科学版，2004，20（4）：459－461／471.Xu Hua，Yu Yong.A practical heuristic optimization algorithm to improve resource balancing［J］.Harbin University of Commercec（Natural Science），2004，20（4）：459－461／471.

［8］葛树斌.汽车二级维护作业流程优化仿真模型研究［D］.长春：吉林大学机械科学与工程学院，2011.Ge Shu－bin.Research on simulation model for process optimization of vehicle maintenance［D］.Changchun：College of Mechanical Science and Engineering，Jilin University，2011.

［9］罗春，杨军.基于遗传算法和覆盖率驱动的功能验证向量自动生成算法［J］.应用科学学报，2005，13（4）：375－379.Luo Chun，Yang Jun.Based on genetic algorithms and coverage－driven functional verification vector generation algorithm automatically［J］.Journal of Applied Sciences，2005，13（4）：375－379.

［10］徐永能，刘述芳，施树明，等.遗传算法在车轮定位参数测量中的应用［J］.公路交通科技，2001，18（2）：52－55.Xu Yong－neng，Liu Shu－fang，Shi Shu－ming，et al.Genetic algorithms in the wheel alignment parameters Measurement［J］.Highway and Transportation Research，2001，18（2）：52－55.

［11］Graves S C.A review of production scheduling［J］.Operation Research，1981，29（4）：66－75.