高压柱形气瓶振动特性分析

胡晓龙，秦忠宝，岳应娟，吕秋娟

（第二炮兵工程大学机械教研室，西安 710025）

1 引言

在现代工业生产中，高压柱形气瓶的应用日益广泛，对国民经济的发展有着重要的影响。目前，高压柱形气瓶已经成为石油、化工、冶金、宇航等多个行业的重要设备，然而此类气瓶一旦发生安全事故，后果不堪设想。本文研究的高压柱形气瓶属于野战条件下的车载气瓶。它们不仅要经历高寒干燥、高温潮湿交替作用的极端环境，更要经受车辆在野外道路上行驶时车辆的剧烈振动。根据相关资料［1，2］，汽车振动的频率范围约为0.5～25Hz，而对于具有越野能力的军用汽车来说，振动频率范围为1～90Hz。调查表明，机械振动是引起高压气瓶安全事故不可忽略的重要因素。

目前，板壳振动理论已经成为工程技术发展一个必不可少的理论基础。各种动力机械、飞机、导弹、储油罐、化工容器、高炉主体等等都有各种各样板壳结构。由于它们承受各种振动的影响，使板壳振动问题成为许多工程部件设计与研究的关键。因此，板壳振动理论的发展对于解决振动问题是十分重要的。其中，在压力容器研究中，板壳振动理论得到了很好的应用。王定贤［3］等人根据唐纳尔简化理论，推导了柱形爆炸容器固有频率的计算公式，为爆炸容器振动特性的研究提供了理论支撑。

本文从求取振动环境下高压柱形气瓶的频率和振型入手，通过板壳振动理论计算与ANSYS 仿真分析相结合的方法，研究野战行驶过程所产生的机械振动对气瓶安全性能的影响，为保障气瓶及其相关设备在野外环境下的安全使用提供支撑。

2 板壳振动理论

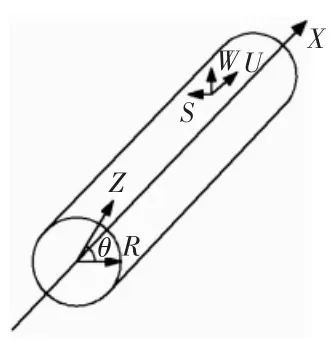
图1 圆柱壳结构示意图

根据板壳振动理论［4］，对于半径为R、长为L的圆柱壳（如图1），取圆柱坐标系为：α=x，β＝θ，γ＝z。

在此坐标系中，圆柱壳简化理论的固有振动方程为

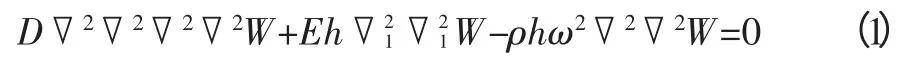
在单向板振动分析［4］中已知两端简支边界条件下的解为正弦函数，因此可以确立振型

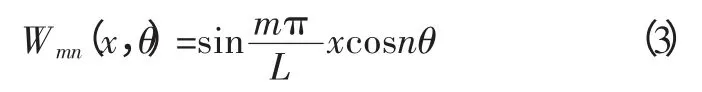
在这种情况下，直接代入简化理论原始方程（1），得到频率方程

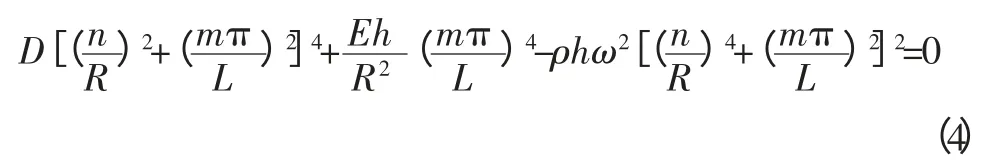
解得频率

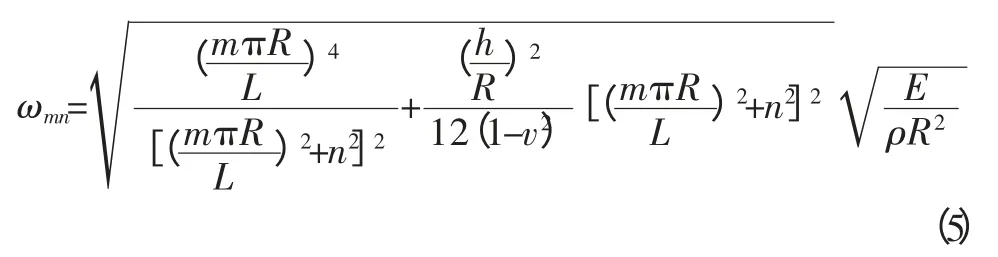
式中，R-圆柱壳中曲面的半径，v-泊松比，h-圆柱壳厚度，E-圆柱壳的弹性模量，ρ-圆柱壳的密度，L-圆柱壳的长，ωmn-圆柱壳的振动角频率，m-相应振型沿轴向有m个半波数，n-相应振型沿周向有n个波数。

从上式可明显看出ωmn由两部分组成：第一部分由薄膜刚度引起；第二部分由弯曲刚度引起，且该式忽略了剪切刚度，ωmn成为薄膜频率和弯曲频率的综合表现。从式（5）还可以看出，影响频率的因素除了材料的力学特性外，还与容器的尺寸、结构和模数有关。

3 公式计算

3.1 气瓶基本参数

图2 气瓶结构示意图

本文研究的高压柱形气瓶为两端收口的圆柱形，如图2 所示，其中间主体部分为薄壁圆筒，两端为近似半球形的封头，主体材料为35CrMo，实测外径Do=0.2212m，平均厚度 h=1.445×10-2m，内径Di=0.1923m，长L=1.9870m，弹性模量E=2.0573×1011Pa，质量m=135kg；根据机械设计课程设计手册，选取泊松比v=0.3，密度ρ=7.9×103kg/m3。

3.2 壳体假设

根据内压薄壁容器设计［5］，通常用容器外径Do与内径Di的比值K 来判断容器是否属于薄壁容器，且有K＞1.2为厚壁容器，K≤1.2为薄壁容器。根据上述气瓶参数，有

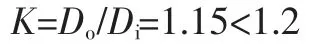
故该气瓶属于薄壁容器，可以运用板壳振动理论进行计算分析。

为了便于分析简化计算，在不影响气瓶基本结构和力学性能，确保计算精度的前提下，对气瓶作如下简化假设：（1）将气瓶假设成为等截面、质量均匀的圆柱筒型壳结构。（2）由于封头为非等截面结构，为简化计算过程又减小计算误差，需要对两端封头进行等效处理。假定封头质量集中在其重心上，为了确保其力学特性不变，计算中采用重心等效法，即把封头重心到主体圆筒端面的距离作为封头的等效长度。在计算时，瓶体长度按等效后的长度值选取，其值为1.8478m。（3）由于螺纹对气瓶整体振动的作用很小，所以忽略了气瓶的螺纹结构。（4）根据实际工况，边界条件采用简支边界，即瓶体端部边界各点的法向与切向移动是约束的，转动与轴向移动是自由的。

3.3 计算分析

为了研究气瓶振动频率与振型变化情况，所以令m，n=1，2，3，4，根据式（3）、式（5）和f=ω/2π 计算得到气瓶的振动频率和振型，将前五阶结果列入表1。

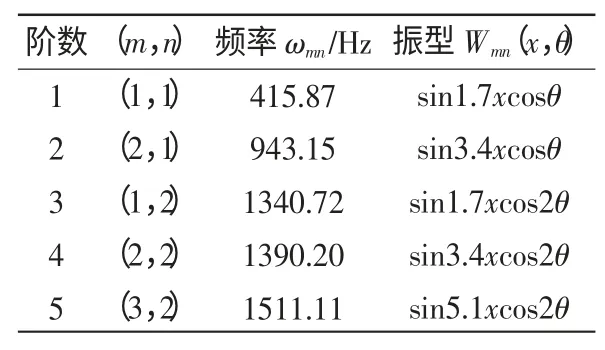
表1 前五阶振动频率和振型

从结果总体变化趋势上可以看出，气瓶的振动频率随着m、n的增大而增大；气瓶在m 保持不变、n 逐渐变大时的振动频率比在n 保持不变、m 逐渐变大时增加得快；当m、n 不断增大，气瓶的振动频率中弯曲频率逐渐处于主导地位。振型振动周期随着频率增大而减小；振型的峰值随着m、n的增大而增多。

4 仿真分析

为了验证以上板壳理论计算准确度，本文使用ANSYS12.0 对气瓶进行仿真分析［6，7］。本次分析采用实体单元Solid45 构建模型。该单元由8个节点定义，每个节点有3个自由度：x，y，z 方向的平动，具有塑性、蠕变、膨胀、应力刚化、大变形、大应变等功能。由于其用于建立三维实体结构模型，误差较小，所以用此单元对气瓶进行仿真建模。为了便于ANSYS 计算，所以假设气瓶为无偏心的理想气瓶，壁厚统一定为平均壁厚，忽略了螺纹影响，保留了封头原有形状，瓶的半径定为中曲面的半径（与第2 节中的曲面相同），弹性模量、密度、质量、泊松比等气瓶基本参数依照3.1 节使用；然后运用自由网格划分，得到较好的网格模型；接着在筒体两端施加简支约束；最后采用求解速度快且较准确的Block Lannczos方法对气瓶模型进行模态分析。

表2 ANSYS 仿真结果

通过ANSYS12.0 对气瓶进行仿真建模，施加约束，模态分析后得到气瓶前六阶的振动频率如表2 所示，各阶振型如图3～图7 所示。

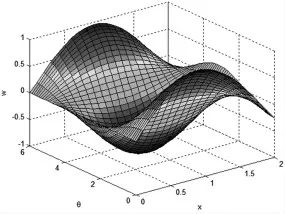
图3 第一阶振型

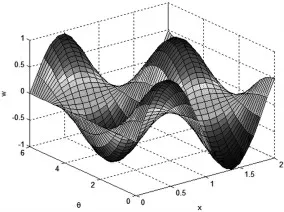
图4 第二阶振型

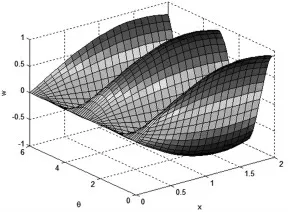
图5 第三阶振型

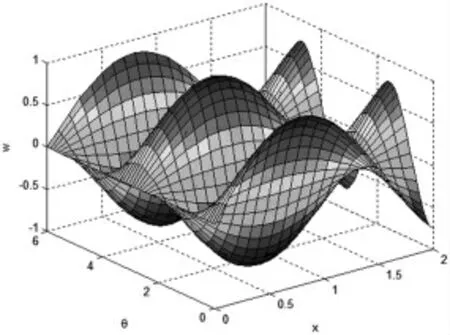
图6 第四阶振型

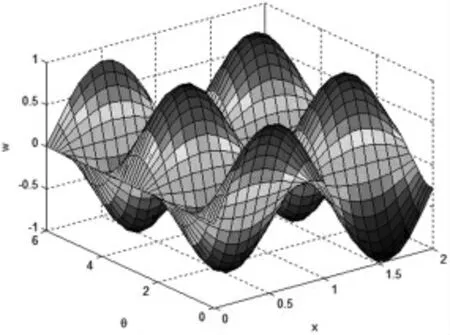
图7 第五阶振型

图8 未变形图

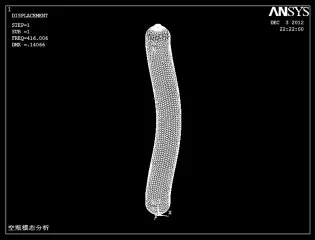
图9 第一阶振型

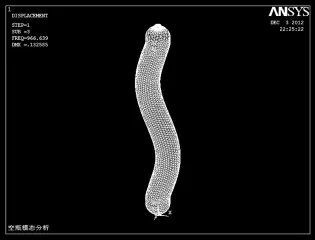
图10 第三阶振型

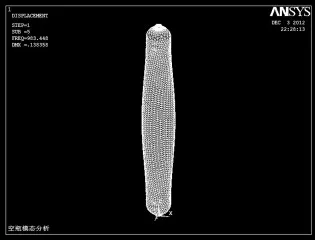
图11 第五阶振型

图12 第六阶振型

从以上图表可以看出，随着阶次的增加，振动频率逐渐变大。由于约束条件的对称性和气瓶模型的轴对称性，使得结果中出现了两个共振频率十分接近的情况，并且它们的振型相似，只是变形的方向不同。由各阶振型的动态显示图可知：第1、2 阶为一个拐点的弯曲振动，第3、4 阶为两个拐点的弯曲振动，第5 阶中间膨胀，第6 阶两端膨胀。

5 结果比较

经过板壳理论公式计算和ANSYS 仿真求解，两种方法计算得到的气瓶振动频率f 如表3 所示。

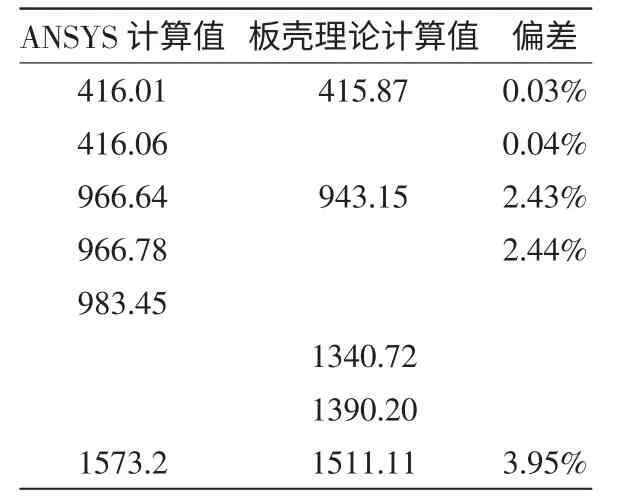
表3 两种方法计算得到的气瓶振动频率比较 /Hz

从表3中可以看出，板壳理论计算结果与ANSYS 仿真结果之间的偏差都在4%以内；两者都存在独自的振动频率；由结果偏差可以看出，两者计算出来的起始振动频率偏差最小。

6 结论

综上所述，经过运用板壳振动理论对柱形高压气瓶进行理论计算，然后用ANSYS 分析结果对这种理论结果进行对比，通过分析所得结论如下：

（1）在用板壳振动理论计算频率时，结果与ANSYS仿真结果比较，偏差都在4%以内。这说明运用重心等效法对气瓶进行振动特性的理论计算是可行的，用板壳理论计算柱形高压气瓶的振动频率是合适的。

（2）板壳振动理论计算中，振型振动周期随着频率增大而减小；振型的峰值随着频率的增大而增多。ANSYS仿真计算的前六阶振型中，有弯曲振动和膨胀两种振动形式。

（3）两种方法计算得到气瓶振动频率都在400Hz 以上，说明使气瓶发生共振的频率比较高。因此，气瓶在车辆振动时不会引起共振危险。

（4）板壳理论和ANSYS 仿真计算的振动频率并不是一一对应的，可能是因为对气瓶进行的假设造成的。即在理论计算时，对两端封头的长度进行了重心等效法的假设，而在ANSYS 仿真求解时保留了封头的原来形状。这将是下一步研究的重要方面。

［1］何锋，杨宁.汽车动力学［M］.贵州：贵州科技出版社，2003：218-271.

［2］李峻岩，等.军用汽车振动性能的仿真［J］.中国科技论文在线，2010，5（10）：807-812.

［3］王定贤，等.柱形爆炸容器的振动特性研究［J］.压力容器，2007，24（11）：6-8.

［4］曹志远.板壳振动理论［M］.北京：中国铁道出版社，1989：263-324.

［5］谭蔚，陈旭，许莉.化工设备设计基础（第二版）［M］.天津：天津大学出版社，2007：82-89.

［6］李晓辉.车用全复合材料CNG 气瓶的安全可靠性分析［D］.北京:首都经济贸易大学，2010.

［7］王正，王磊.焦炭塔结构的固有频率和振型研究［J］.压力容器，2005，22（8）：24-28.