各相独立的ip-iq法APF实现及其控制

黄落成，刘涛涛，王珂，张晓，

（1.中国矿业大学信息与电气工程学院，江苏 徐州 221008；2.中矿传动与自动化有限公司，江苏 徐州 221116）

1 引言

随着电力电子装置等大量的非线性负载在各个领域的广泛应用，使得谐波对电网的污染越来越严重，严重影响了电网的安全稳定运行；而现代信息社会对电能质量又提出了更高的要求，因此如何提高电能质量已经成为电力行业内目前最迫切的问题。APF是一种动态抑制谐波和无功功率的新型电力电子装置，被公认为改善电网谐波问题最有效的手段［1］，而APF的动态补偿效果受到谐波电流的检测精度的直接影响。目前，谐波检测方法大部分都是建立在瞬时无功功率理论［2-5］基础上的。由于ip-iq算法具有实时性强，实现简单等特点，在很多方面都得到了成功的应用。文献［6］对瞬时无功理论在三相4线和单相系统谐波检测中的问题进行了详细地分析，针对问题提出了改进的ip-iq算法，省去了复杂的旋转坐标变换，大大地简化了计算。但是，该文没有对APF直流侧电压控制［7］进行分析，直流侧电压给定值与反馈值的差值经过PI调节后是一个直流分量，在简化的变换中，如何将该直流分量叠加到基波有功分量中，针对该问题，本文进行了分析，提出了APF直流侧电压控制方法，并进行了仿真分析和实验验证。同时，对于改进算法精确的锁相要求，采用了一种基于PI控制的改进数字锁相环，并进行了实验验证。

2 改进的i p-i q谐波提取算法

分析未经改进的ip-iq法发现，Park变换的目的在于将三相电信号变成两相后，继而通过旋转变换获得总的三相有功和无功电流。如果将三相的电流单独进行谐波的提取，对于单独的某一相，就可以省去复杂的旋转变换，这时，只需要按照瞬时无功功率理论中的有功电流和无功电流的定义来构造矩阵C，以获取单独某一相的瞬时有功和无功电流。显然，这种检测方法可以直接用于单相和三相4线的APF谐波检测中。对于三相电流不平衡的系统，一样可以提取谐波指令信号。基于该思路，可以对ip-iq理论进行改进。

设单相瞬时电压和单相瞬时电流分别为

根据瞬时功率理论对ip和iq的定义，定义a相的瞬时有功电流和无功电流为

将式（2）改用矩阵表示：

其中

由式（2）可得，a相与电压同相位的单位余弦信号与瞬时电流的乘积，就是a相瞬时电流在电压上的投影，实际上就是a相的瞬时有功电流，同理即可得瞬时无功电流。

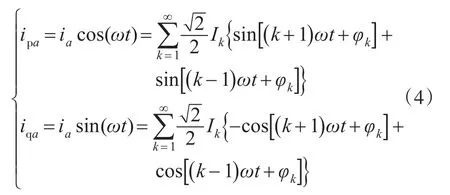
由式（4）可知，当k=1时，ip与iq为1个直流量和2次及以上次数的交流量的和，将得到的ip与iq电流经过低通滤波器LPF滤波以后，即可得到基波瞬时有功和无功电流的直流分量由于ip与iq中含有连续的2，3，4次及以上的谐波，故LPF的截止频率需要取较小的值。显然，当LPF的截止频率ωc取值过小时，系统的响应速度必然减慢；当截止频率ωc取值较大时，提取的基波有功分量中必将含有大量的接近基波频率的谐波，这必然大大影响谐波的检测精度，本文的仿真取ωc=10 Hz。为此，文献［6］对该问题进行了讨论，采用了改进的2阶Butterworth低通滤波器，本文将对截止频率降低带来的检测延迟进行补偿分析。

由式（1）得，当k＝1时，

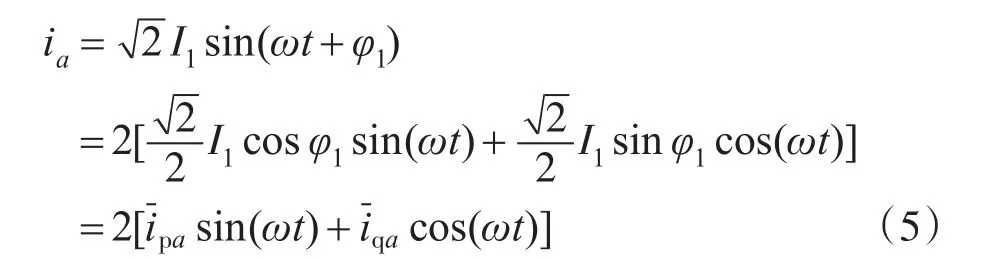
将式（5）用矩阵表示为

其中

由式（6）可以得到a相的基波电流，用负载电流减去基波电流，即可得到谐波电流。谐波检测的原理框图如图1虚线框所示。

图1 改进算法的谐波检测和直流侧电压控制框图Fig.1 The improved harmonic detection and the DC-side bus voltage controlblock diagram

由上面的分析可知，这种方法还可以运用于任意次的谐波检测［5］。设k为所要提取的谐波电流次数，坐标变换中基波角频率ω用kω来代替，则式（4）中最终可以得到的k次谐波的直流分量，通过LPF和反变换便可以得到k次谐波。

3 直流侧电压控制

从图1虚线框可以看出，这种检测方法中没有涉及到APF直流侧电压的控制。由于对单相电流的谐波进行检测，显然不能直接在iˉpa上采用叠加经过PI调节后的电压偏差的方法［1，7］。经过PI调节后的偏差ΔId是整个APF三相基波电流的偏差所致，故应该对三相电流对称叠加与基波同相位的ΔIkf（k=a，b，c）。本文采用的直流侧电压控制方法如图1所示，偏差ΔId与经过同步旋转反变换C-1和C23反变换，即可得到三相与基波相位相同的电流分量ΔIkf（k=a，b，c），将该分量与各相基波电流叠加，即可控制APF直流侧电压。其中C-1和C23分别为

4 基于PI的数字锁相环

由改进算法的原理可得，检测出某一相谐波电流的关键在于准确地获得同相电压信号的相位角。因此，一个准确的易于数字实现的锁相环［8］十分重要。传统的数字锁相有2种方法：一种是基于过零点进行比较的方式，这种方法需要检测电压信号的过零点，当传感器存在零漂或者电压信号畸变时，不能准确的检测过零点。因此，这种方法较少使用。另外一种是基于瞬时功率理论的方法，经过Park坐标变换，当锁相信号准确时，电压在q轴的分量uq为0。因此，可以利用0与uq进行比较，然后通过PI调节器，控制uq为0，即可以实现正序相位的频率锁定。与前者相比，这种方法具有好的鲁棒性，通过调节PI的参数，可以加快锁相的速度。

改进的数字锁相环的原理框图如图2所示。电网电压不平衡时，Park变换后d-q轴存在偶次的负序电压分量，通过引入一阶低通滤波器（LPF），可把电网电压正序分量（直流量）分离出来，这样可以加快锁相的速度。

图2 改进的数字锁相环框图Fig.2 The improved digitalphase-locked loop block diagram

5 仿真实验分析

在前述的理论基础上，建立了仿真模型，并进行了仿真和实验验证。实验采用TMS320F2812+FPGA的控制器。Matlab仿真和实验参数设置如下：三相对称电源线电压有效值为180 V，非线性负载采用三相不可控整流桥带电阻负载，R=4 Ω，非线性负载输出电感L1=0.45 mH，APF直流侧电压Udc_ref=360 V。稳压电容C=2200μF，APF输出电感L=1.5 mH。开关器件的控制采用两电平SVPWM的调制算法，选用两电平IPM功率模块作为变流器，开关频率为12.5 kHz，系统采样频率设为12.5 kHz。锁相环锁相采用DA输出到示波器进行观测。整个系统采用双闭环的控制方法，内环控制补偿电流对指令电流的跟踪，外环控制APF直流侧电压稳定。仿真波形如图3所示。

图3 仿真结果Fig.3 The simulation result

从图3a可以看出，改进的算法可以很理想地提取出负载电流基波，从而可以很好地提取谐波指令电流。从图3b可以看出，本文所采用的直流侧电压控制方法能够很好地控制APF直流侧电压，从仿真理论上验证了该方法的可行性。

实验波形如图4所示。图4中ua表示电网a相电压，is表示电网电流，Udc表示直流侧电压。

图4 实验波形Fig.4 The experimental results

从图4a可以看出，采用本文所提到的直流侧电压控制方法，APF直流侧电压很好地稳定在给定电压值360 V（上下波动5 V），验证了控制方法的正确性。从图4b可以看出，在APF投入前后，网侧电压波形产生了畸变，但是改进的数字锁相环可以很精确地获取电压相位。电网侧电流也得到很好的改善，补偿后谐波含量由23.4%下降到4.7%。

6 结论

本文在理论分析的基础上建立了三相电压型APF的仿真模型，仿真和实验结果验证了改进算法和所提出的直流侧电压控制方法的正确性。这种各相分离的谐波检测方法有如下的优点：1）将旋转变换简化，有利于DSP编程处理。2）各相的有功电流和无功电流得到分离；可以根据需要进行单独处理。3）对于畸变的或者严重不对称的三相电网电压，采用改进的基于PI的数字锁相环，利用改进的谐波检测方法，依然可以准确地检测出各相谐波。4）可以直接运用于单相电网系统和三相4线系统。

［1］王兆安，杨君，刘进军.谐波抑制与无功功率补偿［M］.北京：机械工业出版社，1998.

［2］薛文平，刘国海.一种基于改进型ip-iq方法的有源滤波器［J］.电气传动，2006，36（2）：38-41.

［3］李圣清，朱英浩，周有庆，等.基于瞬时无功功率理论的四相输电谐波电流检测方法［J］.中国电机工程学报，2004，24（3）：12-17.

［4］王建良，崔桂梅，洪晓英.有源电力滤波器谐波及无功电流的检测［J］.控制工程，2003，10（1）：91-93.

［5］王振浩，吴杰，王晓冲，等.有源电力滤波器任意指定次谐波电流检测和控制策略［J］.电气传动，2008，38（11）：77-80.

［6］周柯，罗安，夏向阳.一种改进的ip-iq谐波检测方法及数字低通滤波器的优化设计［J］.中国电机工程学报，2007，27（34）：96-101.

［7］王广柱，洪春梅.多电平逆变器直流侧电容电压的平衡与控制［J］.电力系统自动化，2002，26（11）：23-27.

［8］周卫平，吴正国，夏立.基波相位和频率的高精度检测及在有源电力滤波器中的应用［J］.中国电机工程学报，2004，24（4）：91-96.