四边形阻抗特征值分析与应用
尤田柱
(吉林省电力有限公司辽源供电公司,吉林 辽源 136200)
距离保护的阻抗元件动作特性与保护装置设计原理有关,不同原理特性的阻抗元件需要采用相应的整定计算方法。矢量“模数”概念在常规整定计算中形成了惯性,如果不能建立“向量”思维,多边形特性的距离保护计算过程的“误整定”几率将会增大,这是因为其特征值会影响整定计算结果,需要引起整定计算人员的注意。
1 四边形特性阻抗特征值构成
微机距离保护阻抗有圆特性和多边形特性等形式。多边形特性阻抗保护具有基本特征和扩展特征,扩展特征(第Ⅱ象限偏角、第Ⅳ象限偏角、原点矩形等)属于装置性能本身的内容,与整定计算无关,因此本文仅分析基本特征:电阻整定线倾角、电抗整定线倾角(如图1所示)。
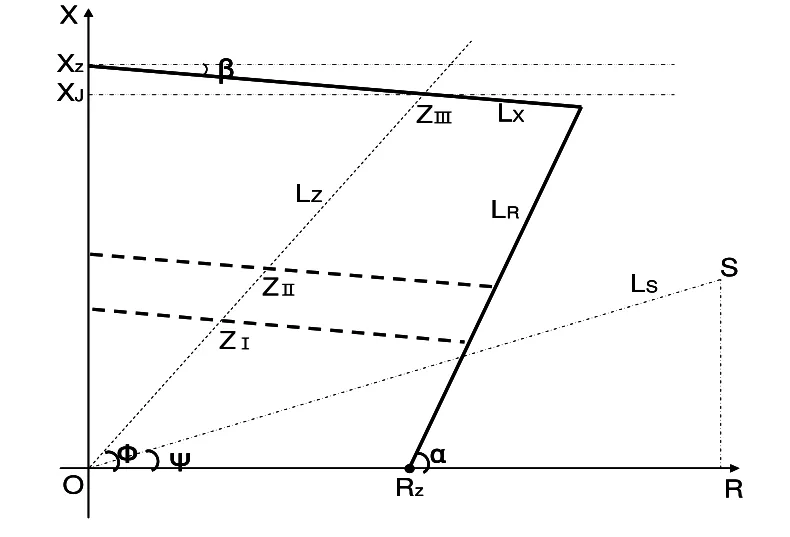
图1 距离保护四边形阻抗特性图
阻抗特性图由电阻R—电抗X二维坐标轴、电阻整定线 LR和电抗整定线 LX围成四边形,其中:电阻特征值体现为LR线的倾角α;电抗特征值体现为LX线的倾角β。对应LR的倾角为α=60°;对应LX线的斜率为tanβ=-1/8,即β=7°。这两个特征值在整定计算和校验时须以重用。
2 四边形特性阻抗特征值应用
2.1 电阻分量RZ值整定及可靠系数Kk选取
RZ分量是躲最大负荷的,整定时不必过于关心实际运行的最大负荷Sm,一般情况仅考虑理论上极限负荷即可。简言之,可以电流互感器额定值确定最大负荷,这是因为,假如实际负荷超电流互感器额定电流时,须更换较大变比的互感器。RZ的计算式为:RZ=Umin/(Kk×Imax),其中:
Umin为母线最小运行电压,可取为 90%的额定电压;Kk为可靠系数,可取为1.8~2;Imax为最大负荷电流,可取为过载50%的极限值。因该项可直接算成二次有名值,对于CT二次额定电流为5A的保护,可直接设定为
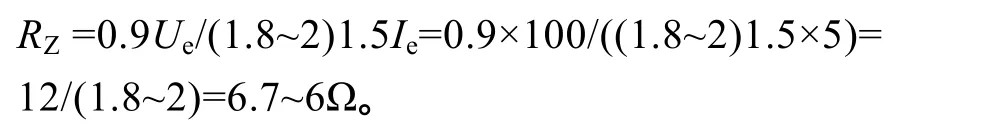
灵敏度足够情况下,建议二次值取为6Ω,以保证任何情况下装置都不会误动作,即Kk值取2。亦即,最大极限负荷阻抗为Zm=Kk×RZ=2×6=12Ω。对于CT二次额定电流为1A的保护,则RZ可取为30Ω。若灵敏度低,且实际最大负荷又远小于极限负荷,则可适当调大RZ。
2.2 电阻分量可靠系数真值返校
电阻分量可靠系数 Kk是以负荷阻抗角按0°计算的原设矢量模值(如图2所示)。
图2 四边形阻抗RZ分量整定校验图
当Kk取2时,最大极限负荷阻抗Zm= KkRZ=2RZ,可靠系数裕量Kδ=(Zm-RZ) / Rz=1。
实际负荷阻抗角Ψ并非为0°,其最大值可按30°(经验值)分析。用LS线表示最大负荷临界线,在LS线与LR线的共同作用下,可靠系数便产生了“变异”,结果使得实际裕量小于1。
用Zm在LS线上的映射等效点S到LR的垂距DS表示可靠系数裕量真值,其大小可通过下列方法求取:
第一步:建立LR和LS两线的函数式,并联立求解,求得交点C(R,X)坐标值。

代数求解得C点坐标:
第二步:求解OC和CS模值大小

于是,所求可靠系数裕量真值为Kδ=DS/RZ=0.134。
还可通过点S到LR线的距离求解更简单(此略)。
由此可知,变异后的实际可靠系数为真值为1.134,与计算时所选定的2发生较大变异。因此,从这个意义上讲,RZ宜小不宜大。
2.3 电抗分量的整定
按整定原则计算的Ⅰ~Ⅲ段电抗分量XⅠ~XⅢ不能直接设定,原因是LX线倾角β使得整定值XZ要大于计算值XJ,需予补偿,补偿度根据β和线路阻抗角Φ换算。四边形阻抗 XZ分量及灵敏度双值图如图3所示。
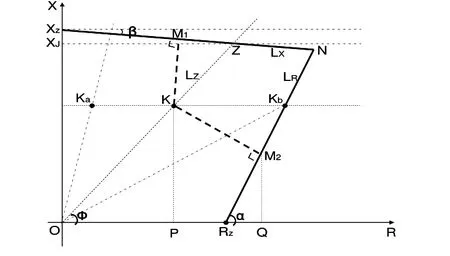
图3 四边形阻抗XZ分量及灵敏度双值图
图3中LX线上Z点对应的X坐标为计算值XJ,而装置整定值则为XZ,补偿值为XZ-XJ。
LX线之倾角 β所对应的斜率绝对值为1/8;Φ为线路阻抗角。于是,借助三角形△ZXJXZ可列出算式:

即,装置的实际整定值为Xz=XJ(1+1/8tan(Φ))。
2.4 电抗分量灵敏度双值筛选
图3所示的K点是阻抗灵敏度校验点,常规校验方法是以OZ/OK为算式,认为灵敏度裕量值是OZ-OK,其结果具有欺骗性。实际上,灵敏度具有“双值”,可用校验点K到两个边的垂距来表示两个灵敏度分量的裕量。由于 LX和 LR两线的数学表达式不同,不能在同一数学表达式中求解,需要分别求算。然后比较两个值的大小,筛选出数值小的来反映实际灵敏度。分析如下:
不同的线路阻抗角Φ所产生的灵敏度“变异”程度不同。点K在水平线上的移动范围,可用左右临界点Ka和Kb表示。配网导线的阻抗角一般在30°~80°之间。导线线径越大,线路阻抗角Φ 越大,Ka越靠近X轴;相反,导线线径越小,线路阻抗角Φ越小,Kb越靠近R轴。不难看出:阻抗角越小,表象灵敏度与实际灵敏度差值越大。且当线路阻抗角Φ较小时,K点可能越出四边形外,此时保护将“拒动”。因此,右临界点Kb作为R分量灵敏度的零值点予以监视。倘若灵敏度校验点K逼近Kb甚至越出四边形外,需要采取相应措施以保证保护装置动作行为(如:抬高Rz值、提出报告、进行技改等)。
自K点分别向两边做垂线,得到垂点M1和M2。用 KM1表示 X分量的裕量,用 KM2表示 R分量的裕量,通过建立数学式分别求解。
X分量的灵敏度裕量可通过下列方法求得:
整定计算时的阻抗综合系数值Kz=OZ/OK,阻抗Z的裕量为KZ=OZ-OK,阻抗Z的裕量比为KZ/OK。
电抗X分量的裕量为
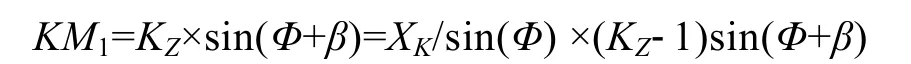
则裕量比KM1/OK,即为X分量的灵敏度裕量δX:

分析:Φ角越小,δX值也越小,“变异”效果就越明显。与 Φ(30°~80°)对应的 sin(Φ+β)值的范围是:0.6~0.9986。亦即,变异后X分量灵敏度裕量是原裕量的0.6~0.9986倍。
例如:整定计算时取用的综合灵敏度系数为Kz=1.5=1+0.5,那么,实际的灵敏度变异为KX=1+0.5×(0.6~0.9986)=1.3~1.4993。
R分量的灵敏度裕量可通过下列方法求得:
利用点K(RK,XK)到LR线的距离公式,导出用XK表示的R分量的裕量,求导过程如下:

即为R分量的裕量。
裕量比KM2/ OK,即为R分量灵敏度裕量δR。(其中 OK=XK/sin(Φ))

分析:K点位置与线路阻抗角Φ有关,Φ角越大灵敏度裕量也越大,最大线路阻抗角(80°)下对应的灵敏度裕量为:0.342+0.852×RZ/XK,此时对应于Ka点;相反,Φ角越小灵敏度裕量也越小,当LZ与LR相交时,对应于交点Kb的灵敏度裕量变为0,该交点定义为R分量灵敏度的“零值”点。零值点坐标的电阻值R0和阻抗角Φ0算式为
R0= RZ+XK/tan(α)其中:XK/tan(α)是 RZKb在 R轴上的投影;RZ是电阻分量整定值。
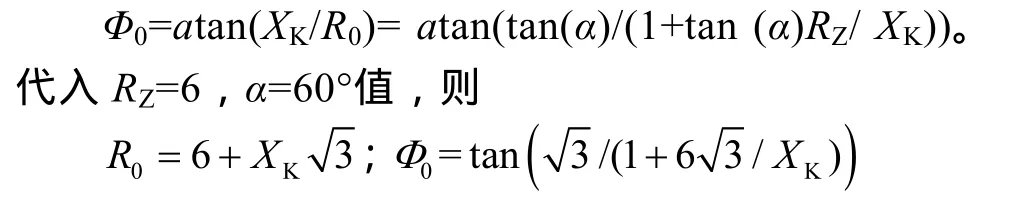
当RK≥R0或Φ≤Φ0时,R分量无灵敏度(进入保护死区)。
从以上求得的电抗分量裕量和电阻分量裕量中筛选出小的用来反映实际保护裕量,min(KM1,KM2)。将其与整定计算时的综合裕量比较,若相差较大,不能保证装置可靠动作时,应采取措施(如:重新选取灵敏度系数整定和校验等)。
3 结论
四边形特性阻抗整定计算不能直将计算值作为装置的整定值;电阻分量整定时的可靠系数不能认为就是实际的可靠系数;保护灵敏度校验方法不能用“模数”算法,需计算双值,选取小者为实际灵敏度。线路阻抗角偏小时,返伪归真效果将更为明显,尤其对阻抗角偏小的配网线路,纠正“模数”算法导致的错误的意义更大。因此,建议在实际整定计算时借鉴或采纳本文提出的算法,还原四边形特性距离保护阻抗元件的本来性能,把住电网安全运行的整定计算关。
本文阐述的观点和方法表面上较麻烦,其实利用保护定值校验工具(如Excel电子表格编辑的工具)编辑为固定算式后则变得非常简单。
[1]崔价佩,孟庆炎,陈永芳,等.电力系统继电保护与安全自动装置整定计算[M].北京:中国电力出版社,1993.
[2]赵志宏,魏会利,田蘅,等.CSL-160C系列数字式线路保护装置说明书[Z].四方继保自动化有限公司,2003.11.
[3]穆大庆.继电保护原理与整定计算.电力系统继电保护与整定计算培训班培训教材[Z].北京国网动经技术培训中心.

