带LCL输出滤波的有源电力滤波器软起动控制研究
胡金高
(福州大学电气工程与自动化学院,福州 350108)
有源电力滤波器(Active Power Filter,APF)作为电力系统谐波补偿的新型解决方案,已成为治理电网谐波污染,使电力系统成为无谐波“绿色电网”的理想选择。通常,将APF设计成电压型有源滤波器,直流侧电容电压的建立和控制是并联型有源电力滤波器实现动态谐波补偿的基础,也成为关键技术之一。
直流侧电压是通过合适的控制,实现交流侧和直流侧之间的能量交换,把直流侧电容电压上升并稳定在某个适当的值,以利用母线电容能量实现对电网谐波的谐波补偿[1]。
APF要求其母线电压在起动和正常工作时应保持其泵升平稳性和稳定性,否则将严重影响其设备的安全性和谐波补偿效果。特别在起动时,充电过程要求平稳,无明显过冲。经过实践可知,直流侧电压变化过程中若控制处理不当,不但产生较大的瞬间电流冲击,本身工作于高值的直流电压还会出现一个较大的超调后才稳定在设定值。在实验过程中发现该冲击电流、过冲电压对于逆变器的电力电子元件造成了比较大的危险,试验过程中很容易出现因为冲击超过逆变器模块电流容量和耐压范围而导致模块烧毁的现象,致使补偿装置不能正常投入运行[2-3]。这严重影响了由电力电子元件所组成的APF的安全性和可靠性。这些现象容易产生的原因主要有如下几个:
1)泵升时母线电压的变化引起等效充电电压系数KE和逆变器PWM电压放大系数KW的非线性变化。
2)大容量APF交流侧电感已变得越来越小,而电网电压在控制中产生较大扰动,电网波动及稍有不慎会产生不可控制的电流冲击。
3)逆变器的脉宽调制规律通常要求直流侧电容电压Ud保持恒定,以计算占空比,变化时不易控制,加上APF具有非线性特性,难于建立准确的模型,使得控制参数选择变得困难。
为了解决这个难题,有关研究人员在文献中提出了各种各样的安全软起动方法[2-3,7-8]。其中提出了直流侧电压的模糊控制策略[4-5],以及提出了模糊和PI的复合控制器设计[6],但这些方法严重依赖于经验,也使系统变得过于复杂而难以应用整定。文献[7]从能量平衡建立模型,并用电压PI控制,通过变比例来适应,但没描述带LCL电流环对起动的影响,文献[9]提出了一种基于同步坐标变换的直流侧电压控制模型,并据此设计出PI控制器,但其模型仅仅从平均功率守恒出发也并没有考虑到电流环中滤波电感的影响。其他文献[10]分析了滤波器软起动的特有特点,采用减少输出电流冲击和泵升电压慢慢渐升的方法,并在特殊情形下使用变PI参数法修正以达最佳效果,但暂没有详细分析。还有许多文献采用斜波缓给定、喇叭口软起动或分段给定方法来抑制上电的电流冲击和电压超调,以克服非线性因素的影响[3],但如果控制模型本质不够稳定,再小的给定也可能会产生较大的冲击,因此对于实际复杂系统的控制效果并不甚理想。
本文在分析APF的电容电压和LCL电流控制环模型的基础上,提出了在网侧电感中串入一个电阻R2,一方面起到安全限流作用,另一方面改善了系统的控制结构和特性,使系统可以更稳定可靠地运行,对此进行了深入的分析。
图1为APF的三相主电路等效图。

图1 三相APF主电路图
1 内环:电流控制特性的改变
母线电压的控制是通过充放电电流来完成的,而电流控制是通过电流环实现的,由于LCL输出滤波器兼顾了低频段增益和高频衰减,所以用LCL滤波器作为并联型有源电力滤波器的输出平波以代替传统的单电感滤波器以提高系统的整体性能。对LCL滤波器而言,虽然减少了总电感、改善了PWM开关纹波滤除能力,但也给控制带来了难度,特别在上电电容电压泵升变化过程中。
电流环如图2所示。其中:Us是网侧电压,L2是电网侧电感,L1是逆变器侧电感,R1是LCL的阻尼电阻,C1是高频电容,E是储能电容,R2是起动串入电阻,Kw为PWM的电压放大系数,Upwm是逆变器侧输出电压。

图2 电流内环控制图
为简化系统的分析复杂性,电流调节器按低频段要求设计成比例控制方式,即

1.1 状态1:没串入电阻R2
在上电充电状态下按常规没接入电阻R2,即主接触器MC闭合后母线电压泵升,则图2中:

1.2 状态2:串入电阻R2
在上电充电状态下,接入电阻R2,即MC断开后母线电压泵升,则
电流环开环的传递函数应为

其中,图2中G2(S)应变为

如R2足够大,基波电流充电下 R2>>ωL2(实验比值为212:1),G2(S)可近似地认为

那么,式(4)电流环开环的传递函数可简化为
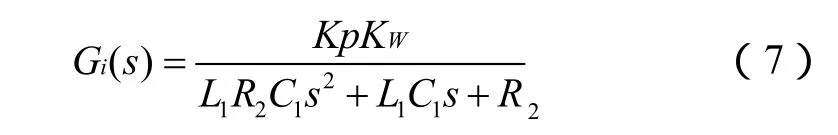
1.3 状态1&2比较:R2加入前后的对比
对比上述式(3)和(7),以及它们的伯德图(图3),可以看出:如加入电阻R2,则系统由三阶变成了近似的二阶系统,其稳定性和相位余量也要好得多,系统便于在电容电压泵升中稳定地控制(在等效逆变器PWM电压放大系数KW和等效充电电压系数KE发生变化时)。
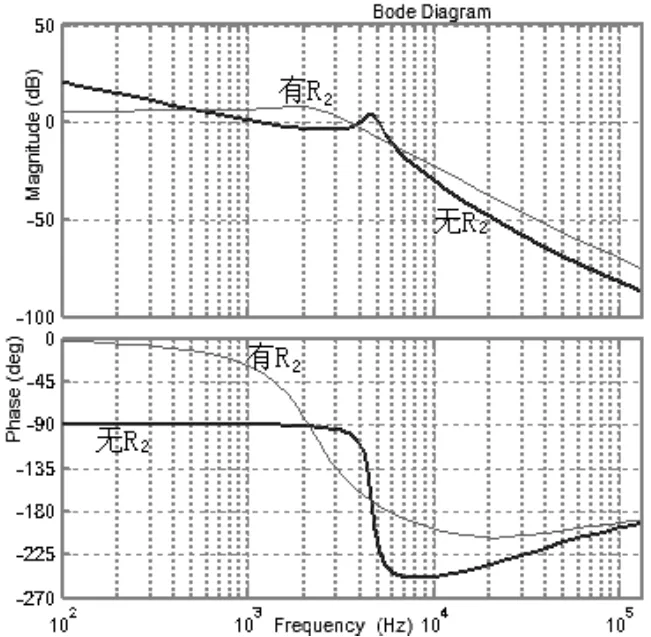
图3 电流环的Bode图对比
图3粗线为没串入R2的Bode图,从稳态来说,电流环中没串电阻近似相当于积分环节,串电阻近似相当于比例环节。对具有3个0dB穿越点的控制对象可能不易通过相角裕度判断闭环稳定性,这里可以辅助采用根轨迹来判断其稳定性,如图4所示。图4(b)中3条根轨迹从左到右分别是R2为5,10,15欧,图3和图4都已考虑入式(4)L2和R1的影响。
显然,带LCL滤波器的电流闭环如没串入R2其稳定范围比串入R2后的稳定性范围要小得多。为了达到泵升电流的正常控制,通常没串入R2必须进行合适的校正,而串入R2可以不需要。

图4 电流环的根轨迹对比
2 外环:电容电压的泵升模型
为了更好地控制电压泵升过程,需要分析有源电力滤波器的电容充电本质。
2.1 推导1依据PWM电路关系
在上电电压泵升和稳定直流电压过程中,系统通过与电网反相或同相的有效值Ip基波电流来升降并维持直流侧电容电压,假设三相进线电压和进线电流

式中,j=0,1,2=a,b,c,表示对应的三相值。
在基波电流充电下,由于 R2>>ω(L 1+L2)
以及 R2<<1/ωc1,可忽略去电感L1、L2压降影响,则泵升压过程应保持如下的电压平衡:

在电容电压Ud下,上管导通的PWM占空比

则a相上部提供给电容器电流ida为
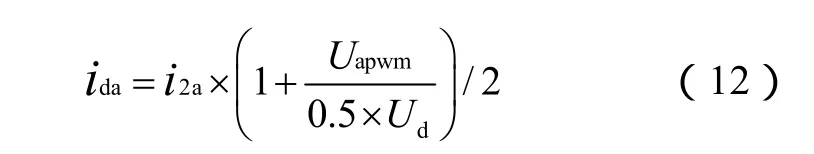
三相上桥臂提供给电容器总电流id
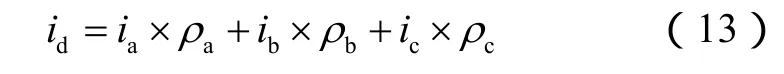
把式(10)至式(13)综合并合简化,并考虑到sin(ωt)+sin(ωt+2π/3)+sin(ωt+4π/3)=0等,可得到

2.2 推导2依据能量平衡关系
如果从有源滤波器电压泵升中的能量交换角度出发[7],由于泵升过程中三相参数平衡并注入对称的控制电流,考虑交流侧电感电容为无功元件并忽略小阻尼电阻R1和逆变桥本身很小的损耗,在dt时间内,电路中的能量分别如下。
交流电网输入
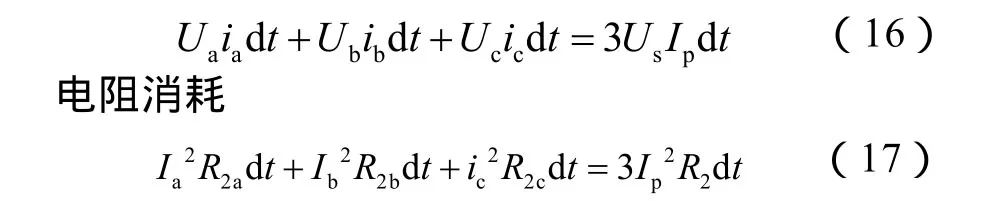
储能电容增加的能量(忽略高次项)

输入电能在电阻消耗后转储于电容上,则
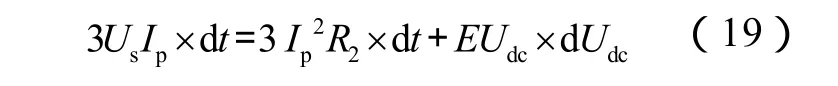
由此可得
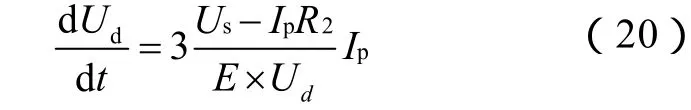
2.3 推导1&2分析电压泵升模型的分析
公式(15)和(20)表明,从 PWM电路关系和能量平衡关系得到的电容电压模型是一致的。可以写成传递函数:

式中,KE为等效充电电压系数,其值不但与电压泵升的电压动态值有关,还与充电电流设定值有一定的关系。
从模型式(22)可知,在上电电压泵升过程中,电流和电压之间有较大的非线性关系,这对电压泵升的控制带来一定的不利影响。
3 上电过程的系统控制
利用上述电压和电流环模型,组成如图5所示的理论模型仿真图。

图5 电压电流双环理论仿真模型
为了避免电压超调,本文的电容电压闭环均采用分离积分控制技术,即比例系数KE不变,积分系数IEi只在直流电压给定值附近时(电压误差△U在50V范围内)才投入,以积分控制消除电容电压的稳态误差,同时消除过早投入引起的调节震荡。利用这个模型对电压电流双环进行理论仿真,其结果如图6所示。

图6 泵升过程理论仿真响应波形
传递函数的理论模型仿真结果表明:上电电容电压泵升变化过程中,充电等效电压系数KE不但变化,而且是非线性变化的;PWM的电压放大系数Kw也是随Ud变化而变化。按照脉宽调制PWM的规律,三相桥的直流侧电容电压Ud应该尽量保持恒定,从而提供一个电压基准进行逆变桥路占空比的控制运算,若直流侧电压Ud波动过大,必须加以动态补偿,增加了控制的复杂性,否则就会出现控制的偏差。
在加入电阻R2后,则电容电压在整流预充电到535V后基本线性地按电流给定限幅10A泵升到电压目标给定值800V,基本没有超调过冲,也无震荡回到维持电压不变的稳定状态。
4 系统仿真与实验结果
由于APF的特殊性,图1中的电网正弦波电压对电流控制产生了很大的扰动,以及逆变器PWM工作的 IGBT桥产生的高频分量对电路也有很大的影响,为了分析实际系统的运行情况,按图1实际系统结构建立如下的系统全仿真模型。
实际系统模型中,上电后主接触器MC保持断开,在不触发驱动逆变器下通过限流电阻 R2和续流管把电容电压预充电到535V;其中在电压达到510V后触发延时3s进入逆变器的PWM导通控制,通过电压电流的双闭环控制把母线电压泵升。如果主接触器 MC闭合泵升就是没串R2的系统,相反主接触器MC仍断开泵升就是串入R2的系统。IGBT逆变桥采用空间矢量控制方式,其施加的空间矢量应该为电网电压矢量与产生特定电流所需的LCL动态压降之和。依据设定直流电压值与实际直流电压值偏差调节产生的充电电流有效幅值Ip〔正或负〕,经过有功环节转化后,产生输出三相与电网电压同步〔反相或同相〕的三相电流给定,通过电流环对最后的储能电容进行充电或放电,以获得最终目标直流电压。
经过仿真发现,设置R2的系统比较容易稳定,调节参数适应性较宽;但对没设置R2的系统不容易稳定,需要不断参数调节优化,最终得出如下结果。
图7(a)为电容直流电压值,其超调的电压低于 2V,图7(b)为网侧电流值,图 7(c)为串入R2=5Ω的电阻瞬时功率,图7(d)为电阻平均功率,以电网周期为时间常数对瞬时功率进行滤波。显然,整个泵升过程较为平稳地进行。
串入电阻的选择可以依据其要求的充电快慢(一般没特殊要求)、设定的充电电流、电阻压降对电路的影响、及消耗功率来决定,以电阻在特定充电电流下对电网相电压220V占用压降<20%为佳。图7仿真以8A充电电流峰值,电阻取5Ω,泵升时消耗功率平均约为300W,由于泵升的电压建立是短时间工作制,可以不必要设置电阻功率安全余量,实际实验时选择80W也是安全的。

图7 串入R2实际系统的仿真波形
在与上述串入 R2相同的实物仿真系统下,闭合MC去掉电阻R进行泵升电压控制,结果如图8所示。图8(a)为电容直流电压值,泵升结束有少许的震荡,图8(b)为网侧电流值,在PWM投入开始由于LCL的滞后特性有段较大电流的冲击难以抑制[13],图8(c)为电压闭环的输出充电电流幅值。由于LCL的稳定度相对差,电流不易控制,引起电压电流的一些调节震荡,有待对之控制方法的进一步校正改进。

图8 没串入R2实际系统的仿真波形
在实物系统上进行实验验证,选取关键参数为L1=500μH,L2=250μH,C1=20μF,Rd=1,R=5。
其实验波形如图9,实验可以取得预期的结果,在设定的电流下平稳无冲击地软起动;图10为不同设定电流下的泵升波形,图10(a)为8A,图10(b)为5A。图11为具有高次谐波非线性负载突变时的电容直流电压变化波形,图11(a)为突加,图11(b)为突卸,在谐波补偿突变时电容直流电压几乎没有变化。
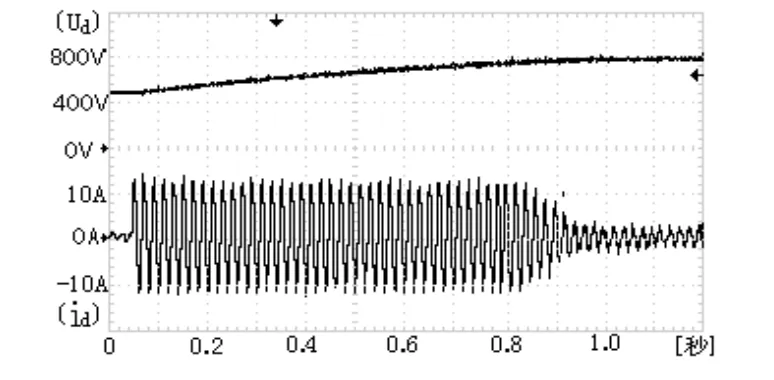
图9 实际系统的泵升波形

图10 不同设定电流下实际系统的泵升波形
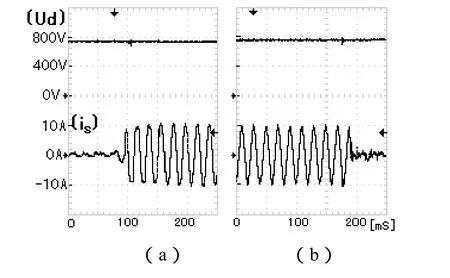
图11 实际非线性负载突变下的直流电压波形
5 结论
本文针对APF进入谐波补偿前,在建立直流侧电容电压时容易出现的电流冲击和电压过冲的问题,提出了一种采用串接电阻实现直流电压的安全软起动方法。通过模型、仿真和试验结果证明,该方法通过改变控制对象特性能有效地减少有源滤波器起动时的直流侧电压过冲和电流的冲击,大大地增加了系统的安全性和可靠性,可以很好地满足有源电力滤波器的正常投入需求,具有较好的工程应用价值。
[1]罗其锋,程汉湘,于树海,张艳.有源电力滤波器双环软起动实用控制策略分析[J].电工电能新技术,2010,29(4)52-55.
[2]王淮生,夏慧峰.并联有源电力滤波器的软起动[J].上海电力学院学报,2011,27[3]:209-219-3.
[3]程汉湘,顾媛媛,刘艺.并联型电力有源滤波器的起动特性研究[J].电气应用,2007,26(3):53-56.
[4]李智华,刘振,吕振彬.有源电力滤波器直流侧电压的模糊自适应控制[J].电源技术,2010,34(6):582-585.
[5]许欢,陈特放,龙占勇.有源电力滤波器直流侧电压控制的研究[J].微计算机信息(测控自动化),2009,25(4):12-13.
[6]何娜,武健,徐殿国.有源电力滤波器模糊软起动控制[J].电工技术学报,2007,22(3)115-120.
[7]李志,杨苹.并联有源电力滤波器的起动建压与稳压控制[J].通信电源技术,2008,25(4): 24-26.
[8]TANG Y, POH CH L, WANG P, FOOK H CH, GAO F.Exploring inherent damping characteristic of LCLFilters for three-phase grid-connected voltage source inverters[J]. IEEE TRANSACTIONS ON POWER ELECTRONICS, 2012, 27[3]:1433-1443.
[9]李俊,王大志,郭喜峰,葛帅.一种有源电力滤波器直流母线电压模糊控制方法[J].电气传动,2011,41(6):23-26.
[10]JOERG D, MARCO L, FRIEDRICH W F. Filter-based active damping of voltage source converters with LCL filter[J]. IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS.2011, 58[8]:3623- 2632.
[11]郭小强,邬伟扬,顾和荣,王立乔,赵清林.并网逆变器LCL接口直接输出电流控制建模及稳定性分析[J].电工技术学报.2010,25(3):102-109.
[12]帅智康,罗安,刘定国,孙贤大,舒适.注入式混合型有源电力滤波器直流侧过电压产生的机理及抑制方法[J]电工技术学报,2008,23(9):144-150.
[13]KHAJEHODDIN S A, MASOVD K G, PRAVEEN K J.A control design approach for three-phase gridconnected renewable energy resources [J]. IEEE TRANSACTIONS ON SUSTAINABLE ENERGY.2011,2(4):423-432.

