针对密码算法的高阶DPA攻击方法研究

赵东艳，何 军

（北京南瑞智芯微电子科技有限公司，北京 100192）

近几年来，针对密码算法的DPA攻击得到越来越多的关注。通过对设备的功耗进行分析发现，密码设备在执行相同指令的情况下，功耗与参与运算的密钥有一定的关系。攻击者利用这种关系对采集到的能量迹进行DPA攻击，可以分析出密钥[1-3]。

为了防御DPA攻击，一种有效的技术是对参与运算的数据进行随机掩码，也称为信息盲化[4]。加了掩码的数据在进行密码运算时，包含密钥信息的中间数据被掩码保护起来，因此能够抵抗一阶DPA攻击。然而这种防御技术仍然可以用高阶DPA进行攻击。相对一阶DPA攻击来说，高阶DPA需要攻击者了解更多的算法实现细节，并且需要选择恰当的攻击模型，所以攻击过程也比一阶DPA复杂得多。

1 能量泄露模型和DPA攻击原理

1.1 能量泄露模型

设备的功耗可以通过在设备的GND管脚和地之间插入一个电阻，然后用示波器测量电阻两端的电压变化来获得。为了建立能量泄露模型，用P[t]表示设备在特定t时刻的功耗。P[t]可以分成两部分，第一部分是与运算相关的功耗d[t]，第二部分是所有与运算无关的功耗n，包括常量部分以及各种噪声。因此P[t]可以表示为[5]：

其中a是刻画d[t]对P[t]贡献度的常量系数。

在指令相同的情况下，与运算相关的功耗d[t]可以用中间数据的汉明重量表示，即：

其中D是密码算法在t时刻的中间值。

根据式(1)、式(2)，设备的能量泄露模型可以表示为：

如果D是均匀分布的随机变量，长度为m位，则W[D]的期望为μW=m/2、方差为σW2=m/4。在统计学理论上，引入功耗P和汉明重量之间的相关系数ρPW来表示上述线性模型的匹配度：

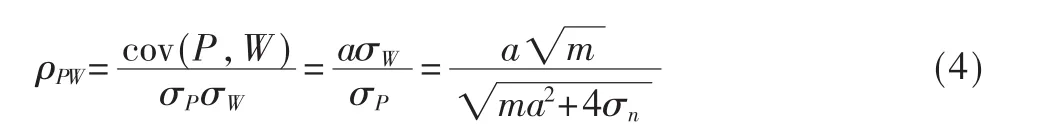
如果在m位中仅s位是可预测的，则功耗和汉明重量之间的偏相关系数为：

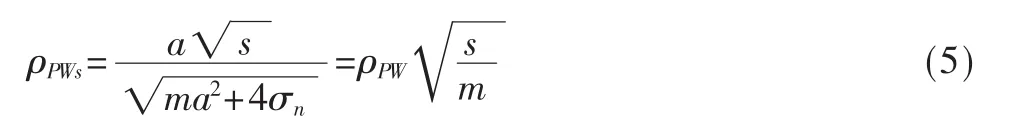
上述相关系数在中间值汉明重量完全正确时达到最大值。

1.2 DPA攻击原理

DPA的攻击理论正是利用功耗与中间值之的相关性，对密码算法的一小段子密钥进行穷举，然后计算在该假设密钥下中间值汉明重量W′和功耗P之间的相关系数。当相关系数达到最大值时，可以推断出假设的子密钥为正确密钥。中间值汉明重量和功耗之间的相关系数计算如下：

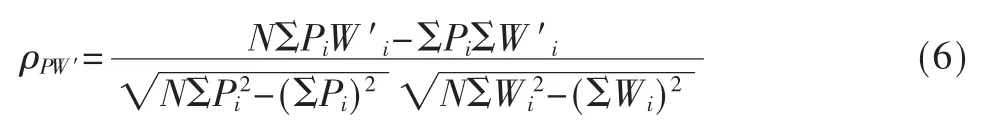
1.3 高阶DPA攻击

1.3.1 高阶DPA攻击原理

高阶DPA攻击的思想是在进行DPA攻击时，同时考虑一条能量迹曲线上的k个点。这k个点对应了k个不同的中间值，应用组合函数将k个中间值组合成一个中间值，然后对新生成的中间值进行DPA攻击，这种攻击称为 k阶 DPA攻击[6]。

1.3.2 高阶DPA攻击的组合函数

组合函数的选择已有相关文献进行过讨论[6]。常见的组合函数包括乘积函数、绝对差函数以及和平方函数等。对于二阶DPA攻击来说，乘积函数计算两点之积，即 comp(tx，ty)=tx·ty；绝对差函数计算两点之差的绝对值，即comp(tx，ty)=|tx-ty|；和平方函数计算两点之和的平方，comp(tx，ty)=(tx+ty)2。

在二阶DPA攻击中，假设被攻击的设备采用布尔掩码，组合假设中间值为ξ＝ξ1⊕ξ2。如果设备泄露汉明重量，可以采用汉明重量模型将组合假设中间值映射为假设功耗值：

分别用 HW(ξ1)和 HW(ξ2)代表能量迹上 tx和 ty两点的真实功耗，两点的真实功耗通过组合函数生成组合功耗P：

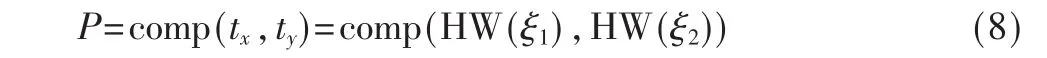
由此可以计算出假设功耗值和组合功耗之间的相关系数：

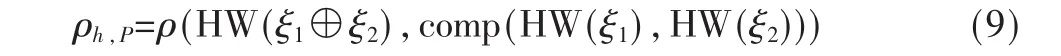
比较相关系数在不同组合函数以及不同中间值位数情况下的差异，可以确定各种组合函数的优劣。

从表1可以看出，在泄露汉明重量的情况下，使用绝对差组合函数能达到更好的效果。

2 掩码技术和高阶DPA攻击

2.1 掩码技术原理

掩码技术的核心思想是使密码设备的功耗不依赖于设备所执行的密码算法的中间值。掩码技术通过随机化密码设备所处理的中间值来实现这个目标。掩码方案可以用下式来表示：

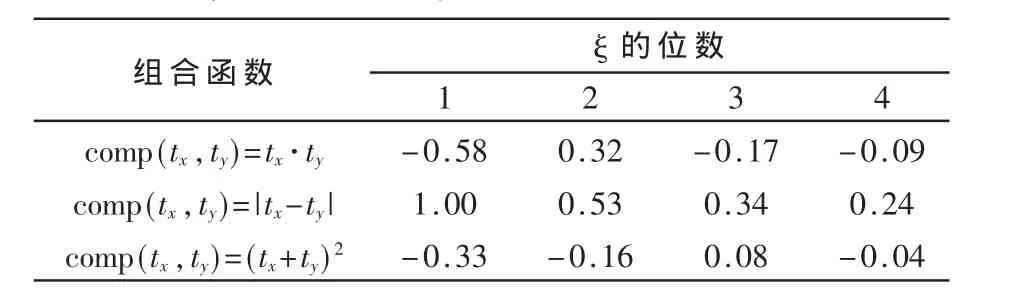
表1 不同情况下的相关系数

其中ξ表示密码运算过程中的中间值；m是掩码，通常是一个内部产生的随机数；ξm是经过掩码的掩码中间值；运算*通常根据密码算法所使用的操作进行定义，一般为布尔“异或”运算、模加运算或者模乘运算。

2.2 DES掩码方案

下面介绍一种经典的DES变形掩码方案[4]。在算法开始时，消息通过64 bit的随机数使用布尔“异或”运算进行掩码。该掩码方案的关键是在每轮开始都带上X1的掩码，为了实现这个目标，掩码方案对S盒进行了修改。修改后的S盒满足以下输入输出关系：

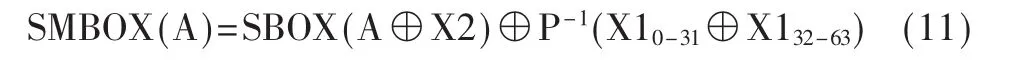
其中P-1表示P置换的逆过程。掩码方案在最后的FP置换之前，将结果“异或”X，消除掩码得到正确的加密结果。计算过程如图1所示。

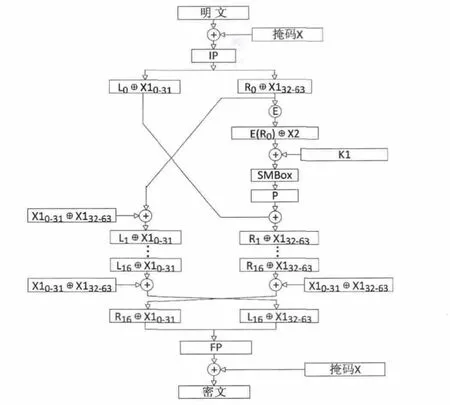
图1 变形掩码方案运算过程

2.3 变形掩码方案的高阶DPA攻击

在上述掩码方案中，整个加密过程每个中间值都带着掩码，因此可以抵抗一阶DPA攻击。掩码方案为了保证每轮运算的结构相同，在轮运算结束时通过非线性的SBOX变换将掩码重新设置为每轮开始的的掩码值X132-63。

根据高阶DPA攻击的原理，可以选择第一轮开始和结束的中间值作为攻击对象，将两点“异或”后得到不带掩码的中间值ξ=R0⊕R1=L0⊕R0⊕P(SBox(E(R0)⊕K1))，如图2所示。

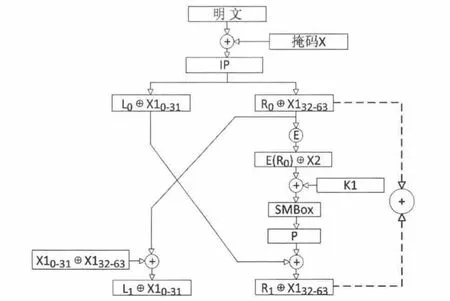
图2 二阶DPA攻击的组合中间值

在S盒的运算结果经过P置换后，每个字节都和所有的48 bit子密钥有关，如图3所示。因此不能直接选择单个输出字节作为中间值。

图3 第一轮运算P置换后的输出结果

在硬件密码设备中，DES协处理器中每轮运算的8个S盒实现是并行的，每个S盒的输出占P置换后的4 bit(1/8长度)，因此不管S盒输出在P置换后位置如何变化，其对能量的影响是始终存在的。如果以一个S盒的6 bit子密钥作为攻击目标，那么在P置换输出结果中除了该S盒的4 bit输出外，其余28 bit输出结果都是噪声。

根据前述的能量泄露模型，6 bit的密钥假设可以达到的最大相关系数为：

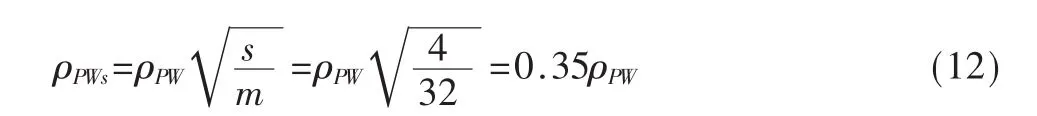
即猜测6 bit密钥时相关系数是猜测全部密钥的0.35倍。为了提高信噪比，可以选择同时攻击12 bit密钥，即2个S盒的密钥。在这种情况下，相关系数可以提高到猜测全部密钥的0.5倍，信噪比会大大提高。

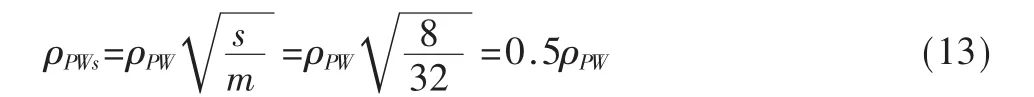
在同时攻击12 bit子密钥时，密钥组合为212个，即需要攻击4 096个假设密钥。

3 高阶DPA攻击实验验证

基于以上分析，对FPGA上实现的带变形掩码方案的DES算法进行了攻击实验。首先在DES运算过程中采集2 000条能量迹，在该能量迹上可以清晰地识别出每轮DES运算过程，如图4所示。

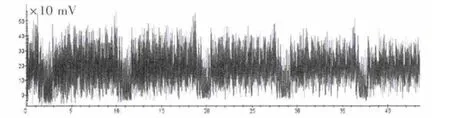
图4 DES运算的能量迹

为了找到每轮运算相同操作（例如S盒运算）间隔的精确时间，采用模板匹配的方法对能量迹进行处理。其原理是首选选择一段具有代表性的模板，然后用该模板与能量迹进行相关性计算，相关性高的位置将会出现尖峰，如图5、图6所示。

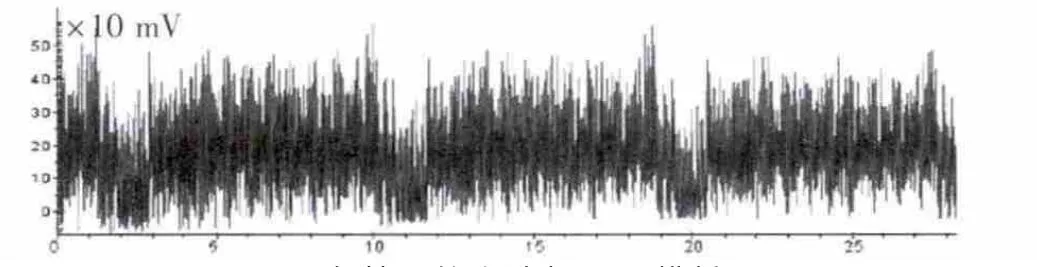
图5 在某一轮上选择匹配模板

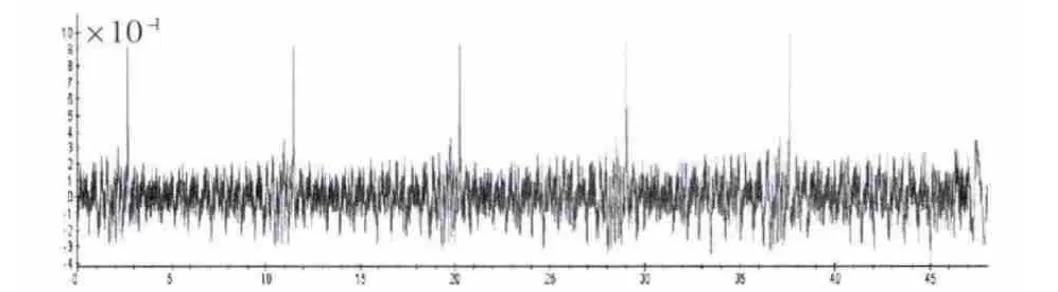
图6 模板匹配相关性曲线

通过测量模板匹配相关性曲线上相邻尖峰的距离，可以计算出每轮运算的时间间隔。在第一轮运算曲线上找出可能出现的所有间隔为σ的两点组合。这些两点组合经过组合函数处理后，形成一条新的曲线。

最后，对组合中间值和新生成的曲线进行相关性运算。在所有4 096个相关系数曲线中，峰值最高的曲线所对应的密钥值就是正确的密钥，如图7所示。在成功获得12 bit密钥后，还需要经过3次攻击共获得48 bit密钥，剩余的8 bit密钥可以通过穷举获得。

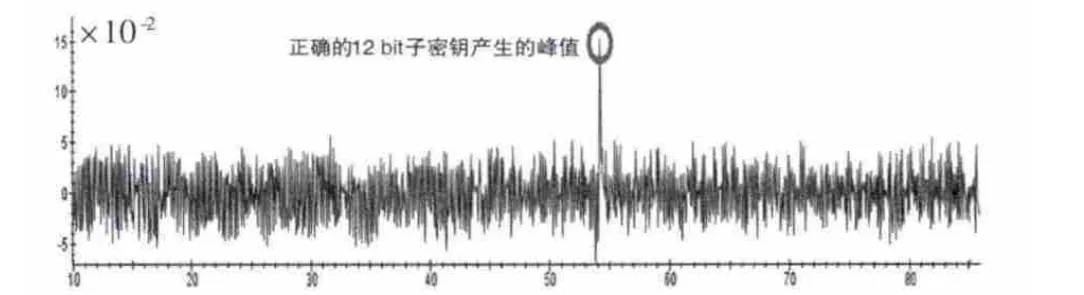
图7 正确的子密钥产生的相关系数峰值

为了抵抗DPA攻击，掩码技术越来越多地被采用。但掩码方案可能受到高阶DPA的攻击，因此在设计掩码方案时，需要充分考虑抵抗高阶DPA攻击的措施。本文首先介绍了能量泄露模型以及一阶和高阶DPA的攻击原理。然后结合变形掩码方案，从理论上证明可以采用二阶DPA实施攻击，并且论述了组合函数的选择以及在攻击中提高信噪比的方法。本文最后在FPGA上对掩码方案的硬件实现进行了攻击实验，并成功获得密钥。

[1]KOCHER P，JAFFE J，JUN B.Introduction to differential power analysis and related attacks[A].Cryptography Research Inc.，1998.

[2]KOCHER P，JAE J，JUN B.Differential power analysis[C].In Proceedings of CRYPTO'99，Springer-Verlag，1999.

[3]MESSERGES T S，DABBISH E A，SLOAN R H,Investigations of power analysis attacks on smartcards[C].In Proceedings of the USENIX Workshop on Smartcard Technology，Chicago，1999.

[4]AKKAR M L，GIRAUD C.An implementation of DES and AES secure against some attacks[C].In Proceedings of CHES'2001，Springer-Verlag，2001.

[5]BRIER E，CLAVIER C，OLIVIER F.Correlation power analysis with a leakage model[C].In Cryptographic Hardware and Embedded Systems-CHES 2004，Springer-Verlag，2004.

[6]MESSERGES T S.Using second-order power analysis to attack DPA resistant software[C].In Proceedings of CHES’2000，Springer-Verlag，2000.