一种结合图像增强的高斯噪声组合滤波算法
余光华
(湛江师范学院信息与教育技术中心,广东 湛江 524048)
责任编辑:时 雯
数字图像在获取过程以及后续的存储、传输等环节中,不可避免地受到噪声的干扰。为了对数字图像进行更好的研究和应用,有必要对图像中的噪声加以抑制,以最大限度恢复图像中的目标细节信息,提高图像的清晰度。干扰图像的噪声种类繁多,主要有高斯噪声、脉冲噪声、瑞利噪声、泊松噪声等,但其中的高斯噪声和脉冲噪声则较为常见。高斯噪声包括电子电路产生的噪声或是由于在照明度低、温度高情形下图像传感器生成的噪声;来源于图像传感器、传输信道、解码过程中产生的黑白点噪声则称之为脉冲噪声,当该类噪声处于饱和状态时,即为椒盐噪声。高斯噪声密度大、噪声强度的波动范围较宽,图像受该类噪声的干扰程度不仅会随着灰度级的不同而有所差异,并且在同一灰度级上也不尽一致,相对于椒盐噪声难以滤除[1]。
抑制图像中的噪声大体上有两类方法:一类是基于图像增强技术的方法,该类方法只需针对图像感兴趣区域采用图像增强方法对图像灰度动态范围加以改善,从而提高图像的视觉效果;另一类是滤波方法,即对图像采用各类滤波方法对噪声加以排除。目前学术界对滤波方法研究主要有以下几个方向:1)单一滤波器及其改进算法,如中值滤波,在此基础上发展而来的加权中值滤波[2]、多级中值滤波[3]、开关中值滤波[4]、极值中值滤波[5]等算法;2)具有严密的数学理论基础的滤波方法,如形态学滤波[6]、小波去噪[7]、偏微分方程去噪[8]等;3)组合滤波方法,即充分发挥各类滤波算法的优势,取长补短对图像噪声进行有效滤除,如文献[9-11]。单一滤波算法尽管得到一些改进,在滤波性能上得到一定程度的提升,但不免增加了计算复杂度,并且每一类算法在提升到一定程度时也难以再有所突破。组合滤波方法相对来说则较为灵活,可针对图像噪声,对各类滤波方法加以有机结合,不但提高了计算效率,滤波效果也较为理想,因此,该类滤波方法具有较好的研究和应用前景。
针对中值滤波对高斯噪声基本无能为力的缺陷,本文尝试对其进行改进,用于图像高斯噪声的抑制处理。将改进中值滤波器与小波域均值滤波器有机结合实现对高斯噪声的逐次滤波。在此基础上,结合图像增强技术,提出了一种具有增强效果的高斯噪声组合滤波算法。
1 本文算法基本流程
1.1 改进中值滤波算法
中值滤波(Median Filter,MF)是一类基于统计排序理论的非线性滤波方法,通过设计一定大小的窗口(滤波模板)在图像中滑动,对图像中某点在窗口中涉及到的所有像素点的灰度值进行排序,取其中间值作为该点的灰度值。因此,能否根据噪声的强度和类型设计合适的滤波模板则成为制约中值滤波处理效果的关键因素。一般来说,模板过大对噪声的滤波效果较为理想,但对于图像边缘等细节信息的模糊也是不可避免的;模板过小尽管不会不显现模糊图像细节信息,但无法尽可能排除噪声的干扰。近年来,学者们针对中值滤波的滤波模板也进行了一系列改进,如加权中值滤波[2]通过对滤波模板中各灰度值赋予一定的权值,进行适当的扩展从而改变模板大小。此外,多级中值滤波[3]对噪声图像进行多尺度逐级中值滤波以尽可能滤除噪声,同时避免图像出现模糊。
鉴于不同大小的滤波模板具有不同的性能,以及受多级中值滤波思想的启发,从滤波模板的角度,对经典中值滤波进行适当改进,对图像高斯噪声进行多角度、多尺度、逐级中值滤波。改进中值滤波方法的基本步骤是:1)分别设计出尺度为3和5的水平和垂直方向的两类一维模板,实现这两个方向的逐级滤波,滤波模板如图1所示;2)经过上述处理后,水平和垂直方向噪声基本滤除,但对角线方向噪声仍存在,并且相对于整幅图像而言,更为孤立,可采用二维3×3滤波进行处理,改进中值滤波基本思路如图2所示。


1.2 小波域均值滤波
与MF类似,均值滤波(AF)也是一类基于模板操作的滤波方法,通过对图像中某一像素点一定大小窗口内的所有像素取平均值作为该点的输出值,从而实现对噪声的抑制,是一种经典的空间域线性滤波方法。当图像中混有加性噪声特别是高斯噪声时,采用AF可快速排除噪声干扰,但对于高强度的噪声,也会导致影像出现不同程度的失真。小波变换能够对图像进行多分度的分解,可以获得高频和低频两类子带图像。并且该两类图像所含信息是不同的,低频图像包含原始图像绝大部分信息,而高频图像则是原始图像高频信息的反映,相对来说,信息量较少。
在1.1节的步骤中,对噪声图像进行改进MF处理,可滤除一大部分噪声,对于混有残余噪声图像,如果仅进行空间域均值滤波处理,则滤波效果也不太理想。小波变换对信号能量具有“集中”的特性,即噪声信号基本集中于高频子图像中,而低频子图像基本不受噪声的干扰。尽管各高频子图像中,高频信息特别是噪声集中于特定方向分布,但总体来说,噪声基本处于孤立状态,因而可对残余噪声图像进行小波域均值滤波,可获得较好的滤波效果。
根据以上分析,本文对经1.1节处理后的图像进行小波域均值滤波处理。具体步骤为:1)对残余噪声图像进行二维多尺度分解(尺度为3,小波基函数为“sym8”),获得低频子图像LL,水平方向高频子图像LH,垂直方向高频子图像HL以及对角线方向高频子图像HH;2)低频子图像LL不作处理,对于高频子图像(LH,HL,HH)分别进行模板为二维3×3和5×5的多尺度逐级均值滤波处理,获得滤波后的高频子图像(LH',HL',HH');3)将高频子图像(LH',HL',HH')与低频子图像LL进行小波重构。
1.3 小波域增强函数设计
对图像进行灰度拉伸,实现图像动态范围有效改善,以尽可能突出图像感兴趣目标信息的处理方法称之为图像增强。图像增强技术大体上有两类:一类是对图像按照一定的函数进行灰度变换,按照函数的类型,该类方法可分为非线性变换、线性以及在此基础上发展的分段线性变换等;另一类是对反映图像灰度分布的直方图进行诸如直方图规定化、直方图均衡化等处理以实现影像增强。图像经过上述处理后,尽管能够取得一定的增强效果,但由于上述方法是对整幅图像采用单个方法进行增强,图像感兴趣目标信息无法有效突出,并且在图像含有少量噪声情形下,上述方法无法在突出图像信息的同时对噪声进行有效抑制。
噪声图像先后经过1.1节和1.2节的滤波后,噪声基本得到滤除,但为了获得灰度动态范围较好的图像,有必要对其进行增强处理。本文受分段线性变换增强方法的启发,将线性变换与非线性变换方法引入到小波域中,提出了一种新型小波域增强函数模型。该函数模型可表示为

综上所述,本文滤波方法主要由3部分构成:1)对噪声图像进行改进MF,以排除一部分噪声的干扰;2)对改进MF后的残余噪声图像进行小波域多级均值滤波处理,基本滤除图像噪声;3)对上述滤波后的图像进行小波域增强处理,以改善图像灰度分布,提高视觉效果。
2 实验与分析
2.1 实验结果评价方法
对于滤波后图像质量的评价,目前大体上有主观和客观两类方法。主观方法主要是人对图像质量进行主观判断,如主观评分法(MOS)、平均主观分数差异法(DMOS)等,但该类方法评价效果受到评价者的专业水平和数量等因素的限制;客观方法主要是采用计算滤波后图像的一些数值指标来实现对图像质量的评价,代表性的有PSNR和MSE等。近年来基于人眼视觉系统(HVS)[12]的评价方法,如结构相似度(SSIM)[13]法得到了一定发展,理论上评价效果优于PSNR和MSE。但由于PSNR和MSE等指标易于编程实现,且计算效率高,数值大小能基本反映出图像质量优劣等特性,仍是主流的评价方法。因此,本文对滤波后图像质量进行主观分析的同时,采用PSNR和MSE指标对其进行客观评价。
2.2 实验结果与分析
2.2.1 改进中值滤波性能测试
为了测试该类改进中值滤波对于高斯噪声的抑制效果,对一幅灰度级为256,大小为512×512的“lena.bmp”图像,加入均值为0、不同方差的高斯白噪声进行测试。定义PSNR值对测试结果进行定量评价,实验结果如图3和表1所示。
对图3和表1数据进行分析可知,图3e清晰度优于图3c和图3d,并且在边缘细节保持方面相对于前两幅图像而言也有一定优势。这体现在表1中,但高斯白噪声方差为0.03时,改进MF优于AM达3~4 dB左右,并且当噪声处于0.09时,改进MF的PSNR值仍高于AM。这可充分表明,改进AM方法,对于图像高斯白噪声的滤波具有较好的效果。

图3 改进中值滤波性能测试
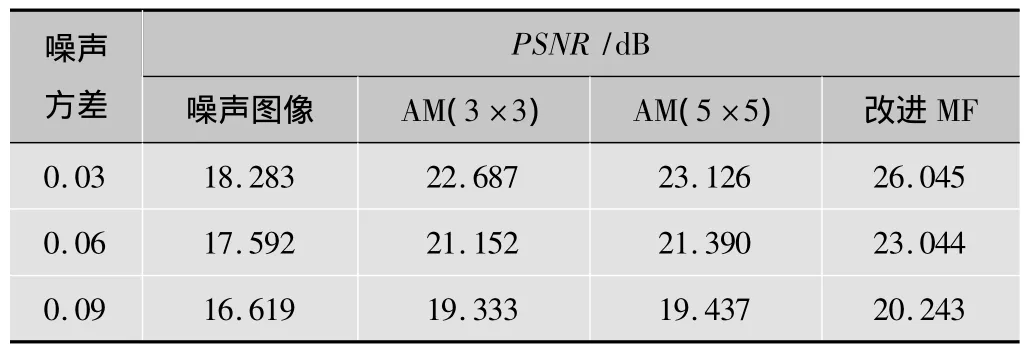
表1 改进中值滤波器PSNR
2.2.2 本文滤波算法性能测试
为了测试本文滤波方法的性能,在MATLAB7.0环境下,编写相关程序对图3a所示的大小为512×512、灰度为256级的“lena.bmp”图像进行滤波实验。通过对该测试图像加入均值为0、不同强度的高斯白噪声,并与文献[1]和文献[9]进行性能比较。实验结果如图4和表2、表3所示;本文滤波方法中,小波域增强函数系数在不同高斯白噪声强度下的取值,如表4所示。

图4 几种滤波方法试验结果

表2 几种滤波方法的PSNR
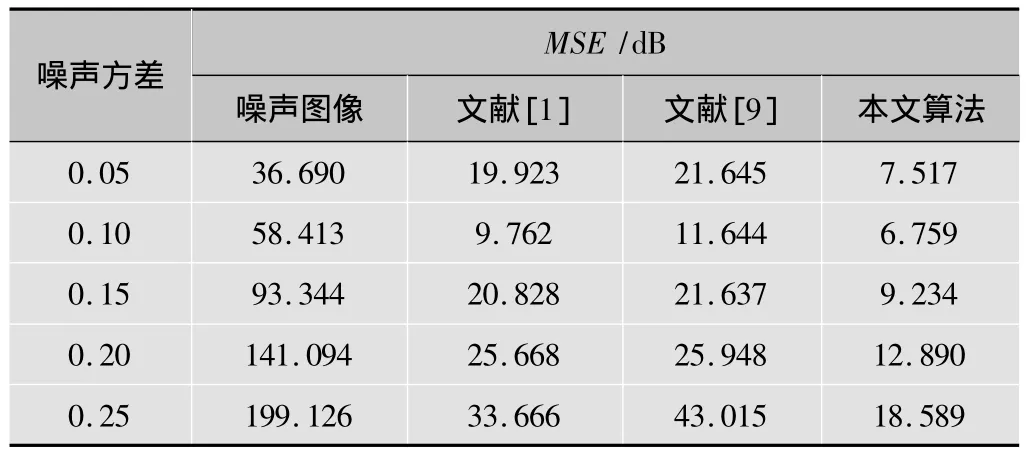
表3 几种滤波方法的MSE

表4 不同噪声强度下小波域增强函数系数取值
对试验结果进行分析如下:
1)滤波实验结果分析
(1)主观分析:噪声图像经过文献[1]和文献[9]滤波后,图像信息集中于较大的灰度级上,表现为图像较为暗淡,并且图像脸部、帽沿等细节信息出现一定程度的模糊,整体视觉效果不太理想;相对而言,图4d视觉效果与原始图像图3a最为接近,灰度动态范围得到有效改善,清晰度优于图4b和图4c。
(2)客观分析:整体上看,无论是文献[1]、文献[9]还是本文滤波方法,当噪声强度逐渐增大时,PSNR值逐渐减少、MSE值持续增大,这表明三者滤波性能伴随噪声方差增大而下降;当噪声方差为0.05时,文献[1]、文献[9]的PSNR值均为21 dB左右,MSE也大体相当,这表明两者对于该水平的高斯白噪声滤波效果基本一致,并且随着噪声强度的增大,这样的“一致”情形一直保持到噪声方差处于0.20时,当噪声方差为0.25时,两者PSNR也仅相差1 dB、MSE值相差10左右;本文滤波方法在噪声为0.05时,PSNR和MSE优于文献[1]、文献[9]滤波方法,分别为5 dB和12~14左右,当噪声方差增大到0.25时,本文滤波方法PSNR值仍高于其他方法2.5~3.5 dB,MSE值低于其他方法15~25 dB,这可以充分说明,本文滤波方法对于高强度的高斯白噪声具有较好的滤波效果,其滤波性能优于文献[1]、文献[9]。
2)波域增强函数系数取值分析
表4数据对不同方差的高斯白噪声进行多项式拟合,可获如下函数关系

式中:x为噪声方差(v);Y(x)为系数a的取值;Y′(x)为系数b的取值。系数a和b取值大体上随着噪声方差的增大而持续减小,特别是系数a取值与噪声方差成典型的线性关系,通过上面两式可对不同噪声强度下增强函数系数进行粗略计算,以获得本文滤波方法在该噪声水平下的最佳滤波效果。
3 结束语
本文针对图像高斯噪声,提出了一种具有增强效果的滤波算法。该算法首先通过对中值滤波进行改进,以实现对噪声图像实现多角度、多尺度逐级滤波处理,以滤除一部分高斯噪声;然后对残余噪声图像进行小波域逐级均值滤波;最后结合线性、非线性图像增强方法提出了一种新型小波域增强函数对滤波后的图像进行灰度动态范围的改善,提高滤波后图像的质量,并结合实验对增强函数系数取值与噪声方差进行多项式拟合,给出了二者的函数关系。实验结果表明,该滤波算法对于高强度的高斯噪声能进行一定程度的自适应滤除,抑制效果较为理想。
[1]王小兵,孙久运.一种新型高斯噪声滤波算法[J].北华大学学报:自然科学版,2011,12(5):606-609.
[2]NASONOV A V,KRYLOV A S.Fast super-resolution using weighted median filtering[C]//Proc.ICPR 2010.[S.l.]:IEEE Press,2010:2230-2233.
[3]贺长伟,刘英霞,任文杰,等.基于多级中值滤波的小波去噪方法[J].计算机应用,2007,27(9):2117-2119.
[4]KUBOTA R,SUETAKE N.Threshold tuning of switching median filter employing distribution distance[C]//Proc.PSIVT 2010.[S.l.]:IEEE Press,2010,427-431.
[5]孙树亮,王守觉.一种基于改进的极值中值滤波算法[J].计算机科学,2009,36(6):165-166.
[6]余永维,殷国富,蒋红梅,等.磁瓦表面图像的自适应形态学滤波缺陷提取方法[J].计算机辅助设计与图形学报,2012,24(3):351-356.
[7]殷明,刘卫.基于四元数小波变换HMT模型的图像去噪[J].计算机工程,2012,38(5):213-215.
[8]郑钰辉,朱立新,王幸平,等.具有纹理保持能力的四节偏微分方程去噪方法[J].计算机工程与应用,2009,45(7):195-198.
[9]王小兵,孙久运,汤海燕.一种高斯噪声组合滤波方法[J].佳木斯大学学报:自然科学版,2011,29(5):696-698.
[10]王小兵,孙久运,汤海燕.基于小波变换的图像混合噪声自适应滤波算法[J].微电子学与计算机,2012,29(6):91-95.
[11]王小兵,孙久运,汤海燕.一种基于数学形态学与小波域增强的滤波算法[J].微电子学与计算机,2012,29(7):64-67.
[12]SHEIKH H R,BOVIK A C.Image information and visual quality[J].IEEE Trans.Image Processing,2006,15(1):430-444.
[13]WANG Zhou.Image quality assessment:from error visibility to structural similarity[J].IEEE Trans.Image Processing,2004,13(4):600-612.

