Mathematica 软件在示波器实验中的应用

熊青玲，潘林峰，程衍富

(中南民族大学 电子信息工程学院，武汉 430074)

Mathematica 软件是美国Wolfram Research 公司开发的数学软件，主要可以做数值运算、符号运算和图像处理。Mathematica 以其简单的语法和强大的功能，成为理工科学生学习数学和物理的重要工具［1］。在Mathematica 新版本中出现的Manipulate命令只用少数的几行输入就能创造出范围极其广泛的人机互动的应用。运用Manipulate 命令不需要学习任何复杂的新概念，也不需要了解任何用户界面的编程思想，只要会使用Mathematica 的基本命令。计算Manipulate 之后得到的输出是一个人机互动的对象，它包含一个或多个控件，使用这些控件能改变一个或多个参数的数值。这个输出很像一个小型应用程序，它不是一个静止的结果，它是一个能和用户互相作用的运行程序。用户可以通过点击和拖拉滑块来观看参数数值和图形的实时变化，也即拖拉滑块的同时数值在变化。本文将Mathematica 的Manipulate 命令用于示波器实验的仿真和研究，具体分析了拍现象和李萨如图［2］。

1 Mathematica 在拍现象中的应用

得到如图1 所示的交互界面，滑动条可以在给定的范围内改变两个信号的频率、振幅和初相。点击滑动条右边的“+”号可以看到滑动条实时的数据。在改变各个参量的过程中，可以看到当两个信号的频率差值远小于频率之和时典型的拍现象。

如果是声振动，当两个频率相近的音叉同时振动时，就可听到时强时弱的“嗡、嗡……”的拍音［3］。在Mathematica 中可以用Play 函数播放声音，输入如下程序:

图1 拍现象

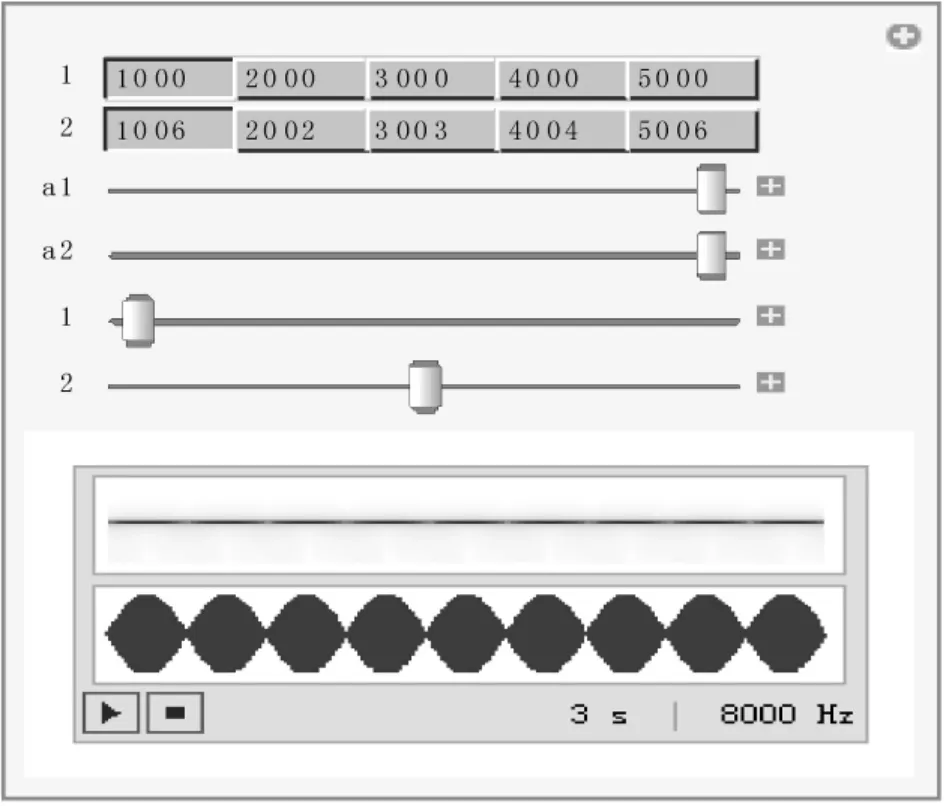
图2 拍音

得到如图2 所示的交互界面，已经根据需要将两个频率给定几组值，任取一组频率可以播放拍音。图2 所示当两个频率分别取为1 000π 和1 006π时，得到拍频为3，在给定的3 s 时间里能听到9 次强音。

2 Mathematica 在李萨如图中的应用与研究

在示波器的X 轴和Y 轴输入频率成简单整数比的两个正弦电压，则将看到特殊形状的轨迹，这就是李萨如图。在Mathematica 中，两个垂直方向的谐振动的合成轨迹就是一个简单的参数函数作图，同样利用Manipulate 命令可以极其方便地作出交互界面。为了进一步研究李萨如图，我们另外采用了一个Point 函数，动态地给出了李萨如图的形成过程。在Mathematica 中输入:

只要我们将两个频率调成不同的整数比，就可以看到稳定的典型的李萨如图，改变两个相位可以看到相位差取不同值时动态的李萨如图。

在实际的示波器实验中，当我们把两个信号发生器的频率调到整数比时，看到的李萨如图往往也是连续变化的。例如:采用数字信号发生器，当X、Y 分别输入ν1=1.000 00 kHz、ν2=3.000 00 kHz的信号时，看到的李萨如图是不稳定的。在变化的过程中，以变化到如图3 所示的形状时为起点，看到中间上面的峰是右移的。

为了找到这种图形移动的原因，在Mathematica 中将ω2的值从3 增大一个小量，ω2的值取为3.04，动画显示出来的轨迹图不再重合。当完成一次完整的图形后，接下来第二次动画完成的图形其中间的峰明显地往右偏移，如图3 所示。当ω2增加的值越大时，这种偏移越明显。反之将ω2从3减小，则情况正好相反，如图4 所示。

这就提示我们，当信号发生器显示的频率为1.000 00 kHz 和3.000 00 kHz 时，实际的频率比不是1 比3，而是与图3 的情况一致。要想让实际信号真正的是1 比3，要么减小频率ν2，要么增加频率ν1。

图3 频率比为1∶3.04 时的图形

图4 频率比为1∶2.96 时的图形

在示波器上实际操作，首先固定X 输入信号不变，微调Y 输入信号，当ν2=2.99 997 kHz 时图像达到最稳定的状态，几乎是不动的。在此基础上把频率朝着减小的方向微调时，发现图像又动起来了，看到中间上面的峰朝左边移动，调得越多，移动速度越快;而把此频率朝着增加的方向微调时，看到的移动方向正好相反。接下来将Y 输入信号固定在ν2=3.000 00 kHz，微调X 输入到ν1=1.000 01 kHz 正好是最稳定的状态;然后分别朝增加和减小的方向调节频率，也同样可以看到图像分别朝不同的方向移动以及移动速度的变化。前后两组数据之比可以写成等式:

1.000 00/2.999 97 =1.000 01/3.000 00

这说明两个信号发生器产生的频率与实际显示的数值存在微小差异。

文献［4］利用MATLAB 软件进行作图，解释了图形的移动变化是由频率与理想频率存在差异引起的。现在利用Mathematica 的动态作图，更加形象直观地显示:当两个分振动的频率比接近简单的整数比时，合振动的轨迹将按照相位差连续变化所得的图形顺序连续地过渡重复变化。在实际的实验操作中，无论是模拟信号发生器还是数字信号发生器，在调节李萨如图的过程中，可以根据图形的移动情况对频率进行微调。在对应图像左移和右移的转折点处所对应的频率，就是图形最稳定的频率。只要仔细地调节，可以将李萨如图调到最稳定的状态。

3 结束语

利用Mathematica 的Manipulate 命令作图，只要掌握Mathematica 的几个简单的函数就可以了，其语法格式与数学书写习惯几乎一样，对于初学者也是浅显易懂的。在Mathematica 的界面中，我们能同时看到源代码和运算输出的交互界面，可以随时修改源代码，随时输出动态交互结果，这给研究问题带来极大的方便。

［1］董键.Mathematica 与大学物理计算［M］. 北京:清华大学出版社，2010.

［2］程衍富. 大学物理实验［M］. 北京:北京邮电大学出版社，2010.

［3］赵近芳. 大学物理学［M］. 北京:北京邮电大学出版社，2008.

［4］张世功，刘大卫，邰贵江. 振动叠加的理论、实验及其数值计算［J］. 实验科学与技术，2011，9(4):61－62.