基于最小二乘方法的单机测向定位算法

何青益，赵 地

（中国电子科技集团公司54所，石家庄050081）

0 引 言

测向定位是利用对同一目标的示向线进行交叉定位来确定目标的位置。机载测向定位分为多机测向交叉定位和单机测向交叉定位，其中单机测向交叉定位由于具有设备简单和系统相对独立等优点，得到了广泛研究。利用单机在不同时刻测量的多条示向线直接交叉定位算法简单，但是定位结果不是最优［1］；基于扩展卡尔曼滤波（EKF）及其推广的定位算法在滤波初始值估计不准或者测量值有突变时容易发散，性能不稳定［2］；本文引入的基于最小二乘方法的测向交叉定位算法，结合了直接交叉定位算法和非线性最小二乘算法，直接交叉定位获取目标的估计初值，通过最小二乘方法迭代得到更高精度的定位结果。基于最小二乘方法的测向交叉定位算法定位精度高，对测向数据进行预处理，可以实时更新目标的位置信息，是一种稳定性好、定位精度高的定位算法。

1 测向交叉定位原理

两站交叉定位是一种基本的交叉定位方式。如图1所示，两测向站的大地经纬度坐标分别为A1（x1，y1）、A2（x2，y2），辐射源到两测向站A1、A2的来波方位角分别为θ1、θ2，则辐射源所处的地理位置即是2条示向线的交叉点B，设其坐标记为（xm，ym）。

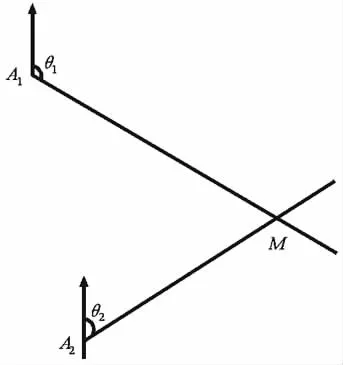
图1 两站测向交叉定位示意图

根据球面三角形的正弦定理和余弦定理，有：

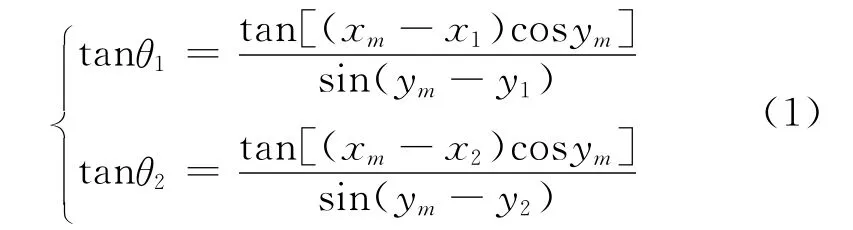
由于待求参数 （xm，ym）包含在多重三角关系中，上面给出的联立方程组没有解析解，只能用迭代方法求出目标的位置，求解信号辐射源坐标的过程分为3步［3］：

第1步：球面基本三角形

测向基础的球面基本三角形由测向站的2条子午线和通过这2个点的大圆构成。在这个基本三角形中，未知数是2个测向站相互的方位角和它们之间的距离。

从A1看A2的方位角θAz1为：

由另一测向站出发计算方位角更简单，应用正弦定理：

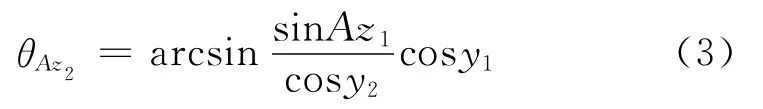
其中的一个角度可能大于180°，必须加以修正。然后计算2个测向站之间的距离z：

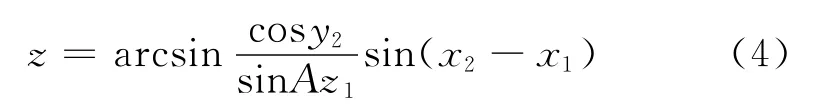
第2步：定位三角形

定位三角形是由测向站基线和2条测向线组成，2条测向线相交于所求的位置点，但从三角形还不能得到该点的坐标。第2步的计算只是为下一步计算提供辅助量，该辅助量是测向站到辐射源的距离，计算出其中一个距离即可：

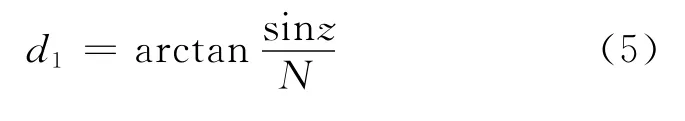
第3步：球面定位基本三角形

此时可利用前面求出的结果计算信号辐射源的经纬度：

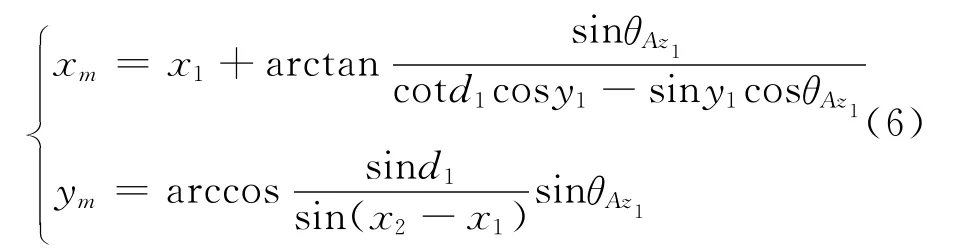
从原理上说，直接测向交叉定位算法既简单又容易实现，但其定位误差较大，主要因为测向站测向误差较大，其中包含系统误差、随机误差2个部分［4］。

2 基于最小二乘方法的定位算法

在飞机运动轨迹上利用测向系统顺序地获取1组辐射源的方位测量值，然后将这些测向数据结合起来估计辐射源的位置［5］，见图2。当不存在噪声和干扰时，对于同一辐射源，方位线精确地相交于一点，该点就是辐射源的位置。但测量误差或干扰总是存在的，同一辐射源2条以上的方位线一般来说不可能确定唯一的交点。因此，为了确定辐射源的位置，就必须对测量值进行一定的处理，获得最优的位置估计。

图2 观测站沿运动轨迹形成的方位线

设飞机在N个坐标已知的位置对同一辐射源B（xm，ym）测向，设飞机第i个位置的坐标为 （xi，yi），测向方位角θi的测量噪声是零均值高斯白噪声，则各侦察位置关于辐射源的观测参量θi与辐射源实际位置B（xm，ym）的关系可写成：

hi（xm，ym）对 （xm，ym）来说是一非线性函数，它可通过在M（xm，ym）的一个初始估计点M0（xm0，ym0）用泰勒级数展开而线性化，保留其前两项可得到公式（7）的线性化表达式：

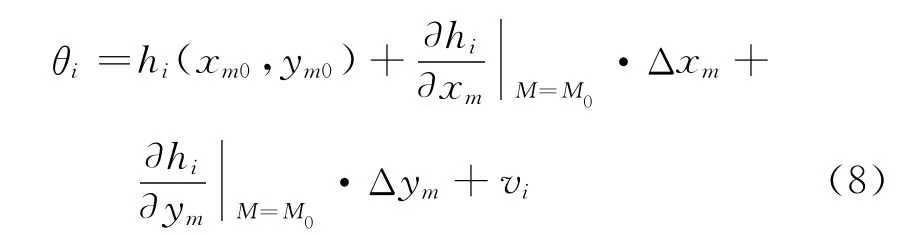
因此式（8）可改写为：

那么，N个观测点的观测方程为：

这样，可以求得W最小二乘估计：

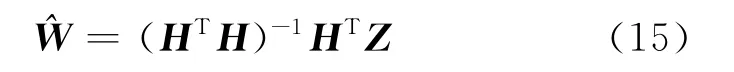
用迭代法可以得到最小二乘估计［6］：

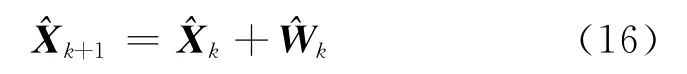
为了开始迭代过程，必须要有一个初始估计值，即k＝0的值。N个位置坐标已知的测向点对同一辐射源进行测向，可获得N条方位线，这N条方位线相交可得到L个交点，L≤N（N－1）／2，对L个交点进行野值剔除、算术平均等处理即可确定精度较高的迭代初始值。

3 算法仿真

设定目标经纬度坐标为（N 38.0°，E 120.0°），飞机航迹的起始点（N 39.347 5°，E 120.000 0°），飞机航迹终点（N 39.030 4°，E 121.109 8°），飞机从起始点沿圆弧朝着航迹终点飞行，在航迹上按经纬度等间隔取120个测量点，飞机航迹上的测量点距离目标的距离150km，飞机绕目标飞过的示向线夹角约40°，测向误差取3°的高斯白噪声。

飞机航迹与目标之间的几何位置关系如图3所示，点代表经过预处理的多个定位结果，＊为直接交叉定位结果，下三角形是基于非线性最小二乘方法的测向交叉定位算法计算结果，五角星为目标的真实位置。

图3 飞机航迹和目标的几何位置关系

通过对飞机多次测量的示向线进行直接测向交叉定位得到目标的估计值（N 38.069 7°，E 120.040 1°），该估计值到目标真实值的绝对定位误差是8.52km，相对定位误差5.68%R（R为辐射源目标到定位站之间的距离）。把直接测向交叉定位结果当作最小二乘的迭代初始值，进行最小二乘迭代运算，得到目标的估计值（N 38.004 4°，E 120.009 5°），该估计值到目标真实值的绝对定位误差是0.96km，相对定位误差0.64%R。由该仿真结果可见，基于最小二乘方法的单机测向定位算法可以大幅提高测向定位精度。

4 结束语

基于最小二乘方法的单机测向定位算法，是在多次观测的基础上寻找能使各次测量数据的误差平方和达到最小的无源定位算法。仿真结果表明，与直接测向交叉定位相比，该算法可以大幅提高辐射源目标的定位精度。综上所述，本文引入的基于最小二乘方法的单机测向定位算法是一种定位精度高、稳定性好、适合工程应用的定位算法。

［1］Wilson Jon.Precision location and identification：a revolution in threat warning and situational awareness［J］.Journal of Electronic Defense，1999，22 （11）：43－48.

［2］Taff L G.Target localization from bearing－only observations［J］.IEEE Transactions on Aerospace and Electronic systems，1997，33 （1）：2－10.

［3］孙仲康，周一宇，何黎星.单多基地有源无源定位技术［M］.北京：国防工业出版社，1996.

［4］王铭三.通信对抗原理［M］.北京：解放军出版社，1999.

［5］何青益，胡东，李艳斌.一种单机对固定目标的无源定位方法［J］.无线电工程，2006，36（10）：33－35.

［6］徐济仁.测向定位中若干问题的探讨［J］.无线电工程，2001（S1）：122－123.