基于方向谱的海浪三维数值模拟

张思将，杨 洁，欧阳艺

（解放军91404部队，秦皇岛066001）

0 引 言

海浪的三维数值模拟从方法上一般分为2类［1］：一类是基于求解流体N－S方程的物理建模方法；另一类是通过参数曲面拟合计算波面高度场的波面造型建模方法。其中，前一种方法求解过程较为复杂，难以达到实时性要求；后一种方法应用较为广泛，相应的实际计算算法也出现多种，如基于随机三角函数叠加［2］、反演海浪频谱合成［3－4］等算法。

本文研究基于Gerstner波的海浪建模方法，并增加波陡度控制参数以改善海浪波形；总结常用的海浪谱和方向扩展函数，分析波浪立体观测计划（SWOP）和Donelan方向扩展函数的异同；计算各子波参数，从而实现3D海浪模拟。

1 基于Gerstner波的海浪模型建模

经典的Gerstner模型从动力学的角度描述了海浪各质点的运动，于1986年被Fournier首次引入计算机图形图像领域，其后被广泛采用［4］。Gerstner波函数为［5］：

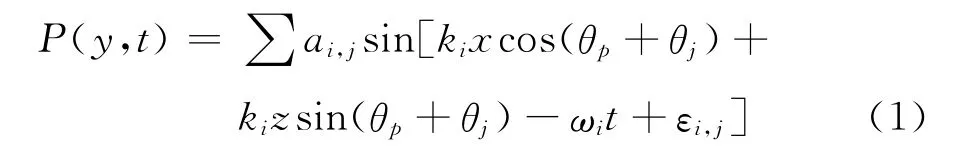
式中：ai，j为子波波幅；θp为风速方向；θj为子波与风速方向的夹角；ki为子波波数；ωi为子波波频；εi，j为子波初始相位。

为了更逼真地模拟海浪，形成较尖的浪头和较宽的浪槽，对Gerstner波的（x，z）坐标进行修正，加 入控制波陡度的参数：

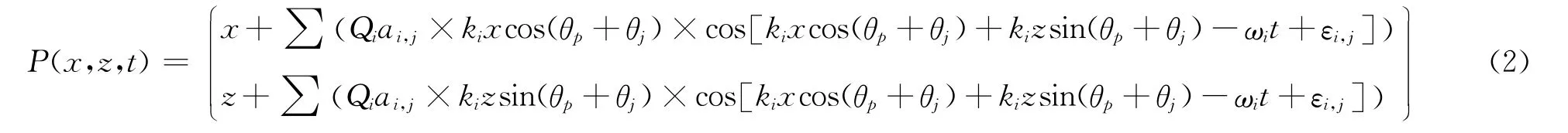
式中：Qi＝Q／（φiAi），Q∈0～1，为波形控制参数。

通过控制Q，即可以得到完全平滑的波到最尖锐的波。由于风是引起海浪的最常见的原因，并且仿真海浪环境一般为深水波，因此将海面简化为风浪深水波。根据线性波理论，对深水波［6］有ki＝

海浪方向谱描述了海浪内部能量相对于频率和方向的分布，一般由频谱S（ω）和方向扩展函数D（ω，θ）组成：

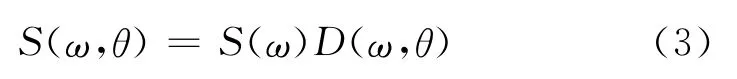
式中：θ为海浪波与风向的夹角。

对于式（1）中的每一个分量，有：

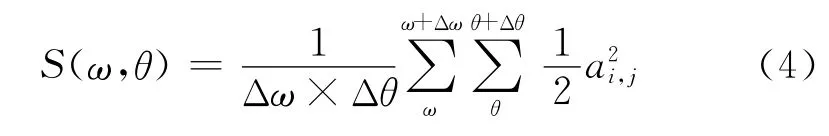
根据式（4）即可求出每个分量对应的子波波幅ai，j为：

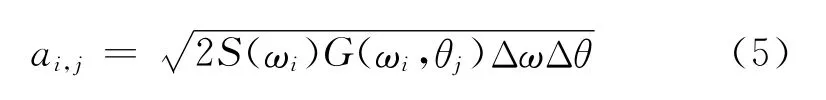
2 构造方向谱

由公式（3），海浪方向谱包括频谱和方向扩展函数，通过组合不同的频谱和方向扩展函数可获得不同的方向谱。

2.1 海浪谱

海浪谱提出于20世纪50年代，它将海浪运动视为平稳随机过程，具有平稳性和各态历经性，通过随机过程理论讨论各种情况下海浪运动的统计性质。目前已提出的海浪谱都是以风要素为参量，用以描述海面风浪状态的。

（1）Neumann谱［7］

Neumann谱是Neumann于1952年最早提出的一种经验谱模式。Neumann认为，在一定风速下的周期可对应不同的波高，但其对应关系有1个上限，他对充分成长状态海浪波高与周期关系进行了拟合，得到Neumann谱的形式：

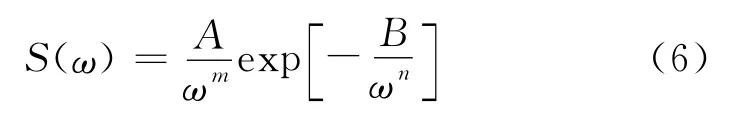
谱高频部分主要取决于前者，而低频部分主要取决于后者，仅限于描述充分成长状态的海浪，而且不具有Fourier谱的性质。至今提出的海浪谱大都属于这种形式。

（2）P－M 谱［1，8］

Pierson和Moscowitz于1964年对在北大西洋充分成长状态下的风浪记录进行谱估计，将得到的54个谱依风速分成5组并将各组谱进行了平均，得到了有因次的拟合式：

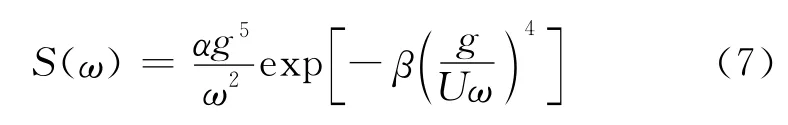
式中：α＝8.1×10－3；β＝0.74；U为海面上19.5m高处的平均风速。

P－M谱是以风速为参量的充分成长状态的海浪频谱。与Neumann谱相比，P－M谱数据基础较好，准确性更好，而且符合Fourier谱的定义，因此被更为广泛地采用。

（3）JONSWAP谱［9－10］

JONSWAP谱是在由德、英、美、荷等国有关组织于1968～1970年进行的“联合北海波浪项目”系统测量的基础上提出的，描述了有限风区持续成长的海浪，其谱式为：

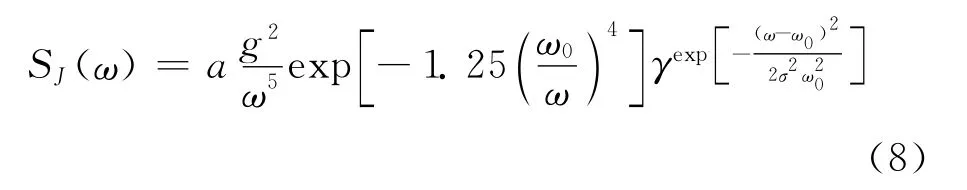
式中：ω0为谱峰频率；γ为谱峰增强因子，即同一风速下谱峰值与P－M谱峰值的比值，其值介于1.5～6，平均值为3.3；σ为峰形参量，用于控制谱峰宽度；a为尺度系数F为风区长度，U10为海面10m高处的平均风速

JONSWAP谱是受限于风区状态的海浪频谱，仅适用于深水，其尺度系数a、谱峰频率ω0和谱峰增强因子γ均与风速和风区有关。当风区很大时，γ趋近于1，此谱也接近于P－M谱。

JONSWAP谱可描述受限于风区的状态，但包含了5个参量，使用不够方便。

（4）其它谱

在海洋学中还常用到其它形式的谱，如Bretschneider谱、Phillips谱、Kruseman谱、Toba谱、文圣常谱等，它们从不同角度对海浪现象进行了描述。

2.2 方向扩展函数

常用的方向扩展函数主要有：

（1）国际船模试验池会议（ITTC）建议的方向扩展函数［2，11］：

（2）ISSC（国际船舶结构会议）提议的方向扩展函数［9］：

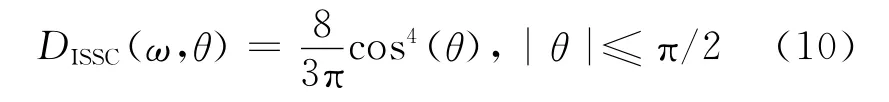
（3）SWOP（波浪立体观测计划）得到的方向扩展函数［9］：

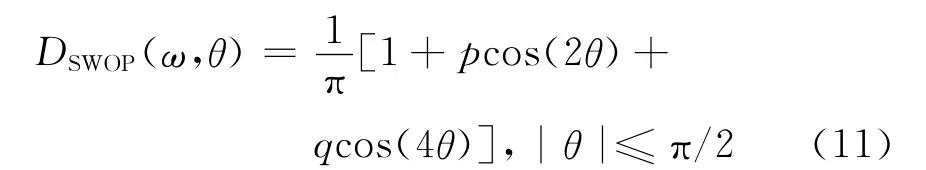
（4）Donelan方向扩展函数［8］

1995年，吴秀杰、滕学春一起根据阵列测量和“956”测波浮标在渤海获得的海浪方向谱资料，从总能量的观点比较了这些海浪方向分布函数，得出在风浪的初始成长和成长状态，Donelan方向分布函数描述吻合程度最好，所以采用不考虑波陡时Donelan方向分布函数：

式中：β为系数；ωp为频谱的峰值频率。

3 方向扩展函数比较

ITTC和ISSC只与子波方向θ有关，具体使用受到一定限制。SWOP和Donelan方向扩展函数充分考虑了子波方向和频谱的关系，吻合程度较好，实际应用较为广泛。

设风速U＝10m／s，ωp＝8.565／U，得到不同频率下方向扩展函数的曲线如图1所示。

选择应用较为广泛的PM谱，分别与SWOP方向扩展函数和Donelan方向扩展函数构成海浪方向谱，计算子波ai，j系数。设风速U＝10m／s，子波方向分别为［－1.047 2，－0.523 6，0，0.523 6，1.047 2］，频率方向上10等分，得到相应的子波系数ai，j，分别如图2所示。

图1 SWOP和Donelan不同频率下方向扩展函数的曲线

由图1可以看出，在ω≤0.5ωp时SWOP方向扩展函数和Donelan方向扩展函数基本相同；在ω＞0.5ωp时，Donelan方向扩展函数更集中于风速方向。由图2看出，计算得到的子波系数ai，j不尽相同，和图1Donelan方向扩展函数更集中于风速方向的结论基本一致。

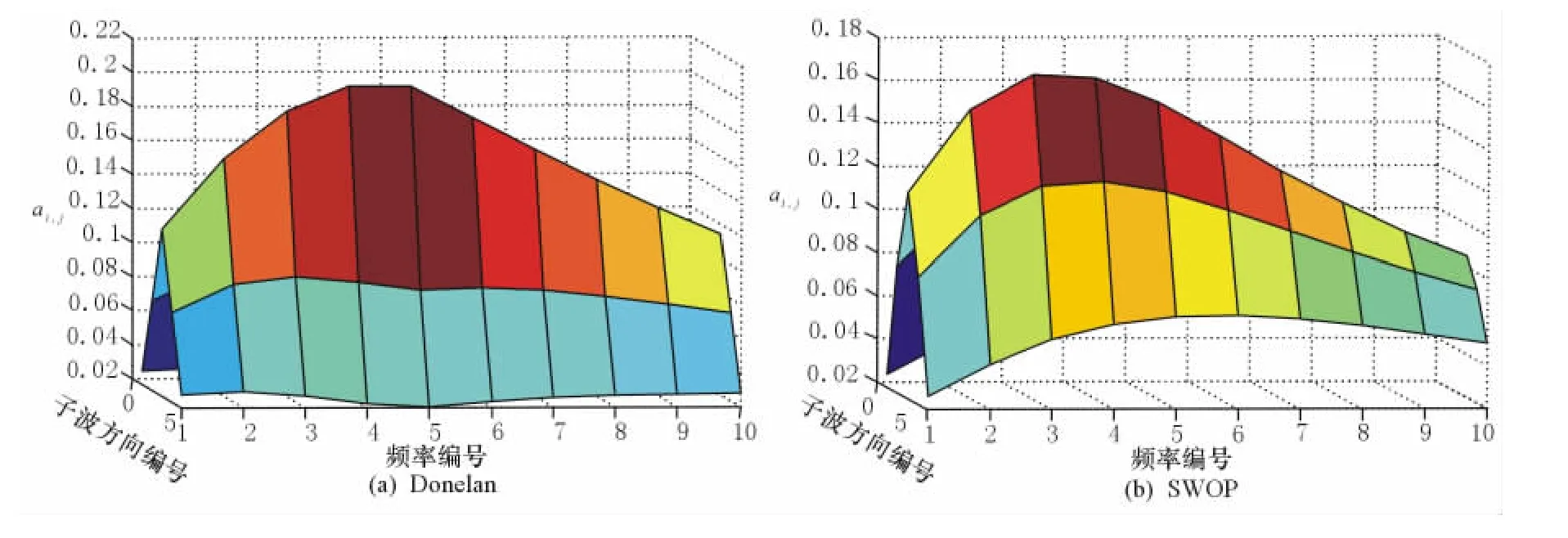
图2 SWOP和Donelan对应子波系数比较

4 仿真实例

图3 动态海面仿真效果

采用PM谱和Donelan方向扩展函数构成海浪方向谱，风速分别选取风速和，渲染得到三维海浪效果，如图3所示。

5 结束语

本文采用Gerstner波建立海浪模型，并增加波陡度控制参数，有效改善了海浪波形；总结了常用海浪谱和方向扩展函数，对SWOP和Donelan方向扩展函数的异同进行了分析；通过计算各子波参数，实现了海浪数值三维模拟。论文仿真结果表明，该方法符合实际情况，效果逼真，具有较高的应用价值。

［1］罗玉，钟珞.基于海浪谱的3D海浪模拟［J］.武汉理工大学学报（交通科学与工程版），2008，32（2）：323－326.

［2］刘洁，邹北骥，周洁琼，等.基于海浪谱的Gerstner波浪模拟［J］.计算机工程与科学，2006，28（2）：41－44.

［3］陈虹丽，李爱军，贾红宇.海浪信号的实时仿真和谱估计［J］.电机与控制学报，2007，11（1）：93－96.

［4］聂卫东，康凤举，褚彦军，等.基于线性海浪理论的海浪数值模拟［J］.系统仿真学报，2005，17（5）：1037－1039.

［5］姚勇，王小琴.GPU精粹——实时图形编程的技术、技巧和技艺［M］.北京：人民邮电出版社，2006.

［6］徐彬.海洋波浪的动态可视化研究与实现［D］.青岛：中国海洋大学，2006.

［7］林乔木，张永刚.基于海浪谱的海浪视景仿真技术［J］.海洋技术，2010，29（1）：109－111.

［8］朱加勇，周波.基于GPU的海浪仿真［J］.应用能源技术，2009（4）：48－51.

［9］侯学隆，沈培志.基于方向谱的海浪合成方法［J］.系统仿真学报，2010，22（1）：130－134.

［10］王宝龙，康凤举，方琦峰，等.三维随机海浪实时模拟方法研究［J］.计算机仿真，2008，25（9）：208－210.

［11］侯学隆，黄启来，沈培志.基于FFT的海浪实时仿真方法［J］.计算机工程，2009，35（22）：256－258.