非饱和渗流分析在FLAC3D中的实现和应用

周跃峰，谭国焕，甄伟文，樊少鹏，3

（1．长江科学院水利部岩土力学与工程重点实验室，武汉 430010；2．香港大学土木工程系，香港；3．长江勘测规划设计研究院枢纽设计处，武汉 430010）

非饱和渗流分析在FLAC3D中的实现和应用

周跃峰1，2，谭国焕2，甄伟文2，樊少鹏2，3

（1．长江科学院水利部岩土力学与工程重点实验室，武汉 430010；2．香港大学土木工程系，香港；3．长江勘测规划设计研究院枢纽设计处，武汉 430010）

基于FLAC3D内置的FISH语言，对其渗流模型进行了扩展。将实验室测得的原状黄土土水特征曲线，利用MATLAB实现了参数拟合。将拟合参数编写为子程序，在每步渗流分析中加以调用，从而实现非饱和土的渗流模拟。利用该方法与有限元法分别模拟3种边界条件下的一维入渗问题，并比较模拟结果。经验证，结果吻合。其结果对研究非饱和土理论及扩展FLAC3D在非饱和土数值计算方面的应用均具有一定的意义。

非饱和土；渗流；土水特征曲线；FLAC3D；二次开发

1 研究背景

渗流是指水或其他流体在岩土等孔隙或裂隙介质中的流动。非饱和渗流是岩土体中孔隙水的最普遍的一种渗流方式［1］。该问题广泛存在于边坡工程［2］、地基／路基工程［3］、隧道工程［4］中。渗流直接影响作为渗流骨架的岩土体力学性质，因而在岩土工程变形和稳定性分析中占有重要地位。通过非饱和渗流计算能够得到土中水的运动轨迹，并为流固耦合分析提供水分场的分布规律。

FLAC3D是美国ITASCA咨询公司开发的三维有限差分程序［5］。该程序采用显式拉格朗日算法和混合－离散分区技术进行积分计算，可求解地质材料的高度非线性、孔隙介质的应力－渗流耦合、热－力耦合以及动力学等问题。该程序依靠较快的运算速度、强大的前后处理、灵活的FISH语言，在目前的科研及工程领域具有广泛的应用。但是其内置的渗流模块，在进行非饱和渗流分析时并不够完善。由于缺少负孔隙水压力（或基质吸力）同含水量（或饱和度）的关联函数，FLAC3D中负孔隙水压力仅反映土体的剪胀变形［5］。因此，难以直接利用FLAC3D对非饱和土进行准确的渗流分析，一定程度上限制了FLAC3D的应用。李毅等［6］通过为非饱和区赋以很低的渗透系数，运用FLAC3D进行非饱和渗流模拟，提供了一个可供借鉴的方法。但该方法本质上并未考虑负孔隙水压力同含水量或饱和度之间的重要联系，影响求解域中孔压场的演化和进一步分析应力场的分布规律。为了解决以上不完善之处，本文介绍了非饱和渗流分析在FLAC3D中的实现方法。

2 饱和－非饱和渗流理论

国内外许多学者投入了大量的精力，逐渐建立起较为完备的土的入渗理论框架，如Richard［7］，Philip［8］，Lumb［9］，Fredlund［10］等。三维条件下，土体的渗流控制方程可以表示为下式（1）的形式，即

式中：kwx，kwy和kwz分别表示3个方向的渗透系数（m／s）；ρw表示水的密度（103kg／m3）；mw为土水特性曲线的斜率；uw表示土中的孔隙水压力（kPa）。

土的饱和－非饱和渗流问题，至少需要2个基本函数：土水特征曲线和渗透系数函数。其中，土水特征曲线描述了土的含水量随基质吸力或负孔隙水压力的变化；渗透系数函数则表示渗透系数随含水量或饱和度的变化。目前，有多个经验公式可用来描述土壤土水特征曲线，包括：Brooks－Corey模型、Garden模型、van Genuchten模型、Fredlund＆Xing模型等［11］。其中，van Genuchten模型作为较有代表性的公式被广泛使用，即

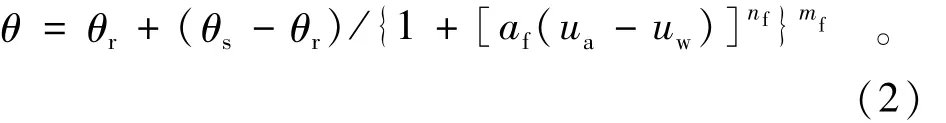
式中：θ，θr，θs分别表示体积含水量（满足θ＝ns；即孔隙率n和饱和度s的乘积）、残余含水量，以及最小吸力含水量；ua和uw分别表示孔隙气压力和孔隙水压力；af，nf，mf为拟合参数。

非饱和土的渗透系数函数大多描述了非饱和土渗透系数与饱和土渗透系数的关系。在数值模拟中较多采用的一个公式［4，12］，可表示为

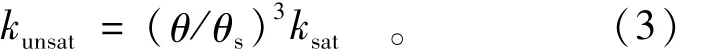
式中：ksat和kunsat分别为土的饱和渗透系数和非饱和渗透系数。

3 饱和－非饱和渗流分析在FLAC3D中的实现

3．1 曲线拟合

土水特征曲线的测试方法较多，包括：体积压力板法、盐溶液法、Tempe仪法、滤纸法、GDS四维应力路径法等［13］。实验室测量的结果通常都是基质吸力同含水量相对应的多个离散点。鉴于土水特征曲线的连续性，需要对由实验室试验测得的离散点作进一步分析，获取数值模拟所需的基本参数。实验室中测得的离散点可利用Matlab R2010写执行脚本作曲线拟合，步骤如下：

（1）创建一个新的M－文件，并输入van Genuchten公式，

function F＝fun（x，xdata）

F＝x（1）＋（x（2）－x（1））．／（1＋（x（3）*xdata）．＾x（4））．＾（1－1．／x（4））。

（2）在命令窗口分别输入试验测得的基质吸力和体积含水量，

xdata＝［x1 x2…xn］；

ydata＝［y1 y2…yn］。

（3）为迭代计算赋初值，

x0＝［0．1，0．1，0．1，1］。

（4）利用函数拟合试验数据，获取拟合参数，

［x，resnorm］＝lsqcurvefit（＠fun，x0，xdata，ydata）。

此时，可在工作区获得相应的拟合参数，亦可在工作区绘制出拟合图形。

3．2 算法的修正思路

非饱和土的渗流问题是一个非线性问题，渗透系数、孔隙压力、逸出面范围等只能在计算过程中迭代确定。渗透系数会受到颗粒级配、孔隙率、饱和度等因素的影响。对饱和土体，渗透系数通常简化为常数；而对非饱和土体，渗透系数可能因含水量的变化而变化很大。根据第2节所述，修正中需考虑负孔隙水压力及渗透系数随含水量的变化。需要注意的是有限差分程序中，渗透系数是单元变量，而孔隙水压力是节点变量（单元孔隙水压力为各节点值的映射）。

数值计算步骤如下：①设置求解域的边界条件和初始条件（如节点的孔隙水压力）；②在程序中指定土水特征曲线（按上述Matlab拟合结果）和渗透系数函数；③根据土水特征曲线，将节点的孔隙水压力转化为节点的饱和度；④计算一个渗流时步，按照质量平衡方程，各节点含水量在计算中发生变化；⑤根据土水特征曲线，将新的节点饱和度转化成为节点的孔隙水压力；⑥按照单元中的各节点的孔隙水压力和饱和度，映射得到该单元的孔隙水压力和饱和度；⑦按照该单元的饱和度，确定相应的非饱和渗透系数；⑧计算下一个渗流时步。

4 算例和程序验证

为了验证上述方法的正确性，本研究中，利用GEO－STUDIO软件中的有限元程序SEEP／W的计算结果与有线差分程序FLAC3D的计算结果进行对比。GEO－STUDIO是一个二维的岩土工程仿真分析软件，其渗流模块发展较为成熟，应用较广泛，但是，它只局限于二维渗流计算，不能进行三维分析并且在其与SIGMA／W进行耦合计算时常出现收敛不理想的情况。

图1 基于FLAC3D和SEEP／W的计算模型Fig．1 Num ericalmodel built in FLAC3D and SEEP／W

本研究中，分别利用FLAC3D和SEEP／W建立相同尺寸的一维模型。模型长度10 m，包括50个计算单元（图1）。程序验证中共模拟3组算例，分别比较了3种条件下2个程序的计算结果。

本文的土水特征曲线是在GDS公司生产的非饱和三轴仪上进行增湿试验，利用轴平移技术测得的原状黄土的基质吸力和含水量的关系。并按照第3．1节中所述方法，将实验室测试得到的土水特性离散点在Matlab程序中进行曲线拟合（图2）。黄土的饱和渗透系数通过现场双环注水试验测得。测试过程详见笔者的博士论文［14］，在此不作赘述，相关参数概括于表1。根据拟合结果，该黄土残余含水量为8．7%，饱和含水量为40．7%；由于采用增湿曲线，不对该黄土进气值进行分析。

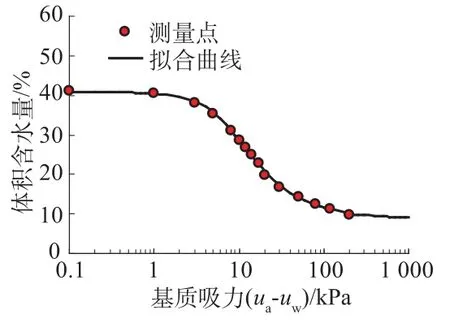
图2 测量及拟合的土水特征曲线Fig．2 Measured and fitted SWCC

表1 算例中采用的参数Table 1 Parameters adopted in the simu lated cases

3组算例中，底部边界均设为恒定孔隙水压力为－147 kPa（－15 m水头）。顶部边界设置为：①算恒定的压力边界条件为uw＝0 kPa（例1）；②恒定的流量边界条件为q＝0．75 ksat（例2）；③算恒定的流量边界条件为q＝2 ksat（例3）。

为了合理比较FLAC3D和SEEP／W的计算结果，数值模拟过程中还注意了以下条件：①相同的单元形状和尺寸；②相同的土水特征曲线和渗透系数函数；③相同的初始条件（各节点孔隙水压力均为－147 kPa，即－15 m水头）；④相同的时步（10 s）。每组算例中均模拟了4种不同时长，即：20 000，40 000，60 000，80 000 s。针对不同时长，分别比较了2个程序的计算结果。

图3—图5为利用FLAC3D和SEEP／W模拟的孔隙水压力和体积含水量（反映浸润范围）在不同的模拟时间下随深度的分布情况。可以看出：在不同的算例中，分别利用修正后FLAC3D和SEEP／W进行数值计算，在不同的计算时间下二者的模拟结果均较为相符。模拟结果表明运用本文方法对FLAC3D的渗流模型的修正合理，且导入的土水特征曲线有效。2个程序计算结果的微小差异可能是由于有限差分法和有限元法计算方法精度的不同所导致。

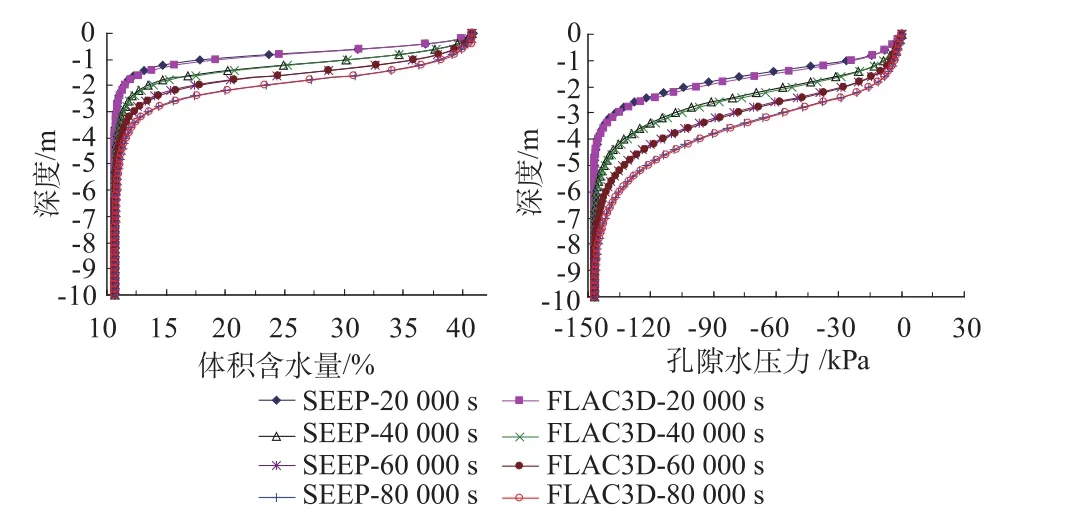
图3 uw为0条件下的体积含水量和孔隙水压力随深度的分布曲线Fig．3 Distributions of volumetric water content and pore-water pressure w ith depth（uw＝0 kPa）

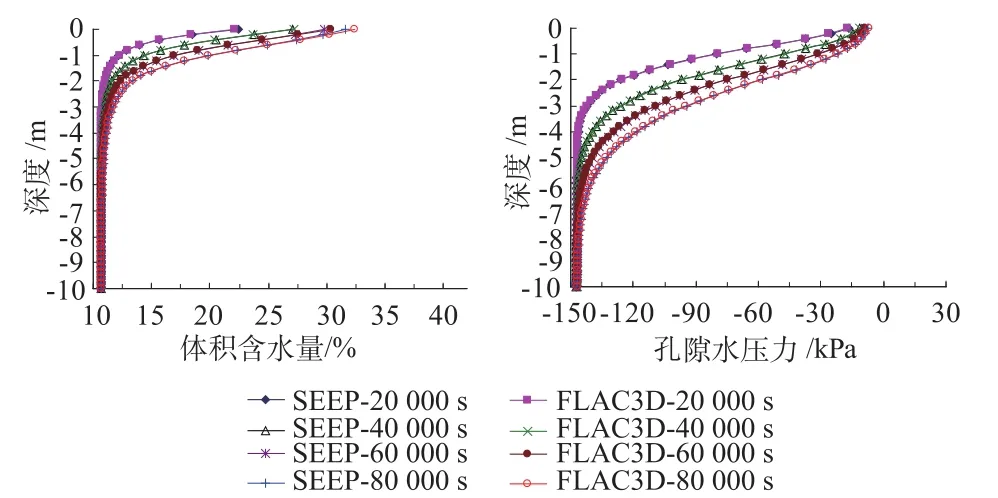
图4 q为0．75ksat条件下的体积含水量和孔隙水压力随深度的分布曲线Fig．4 Distributions of volumetric water content and pore-water pressure w ith depth（q＝0．75ksat）

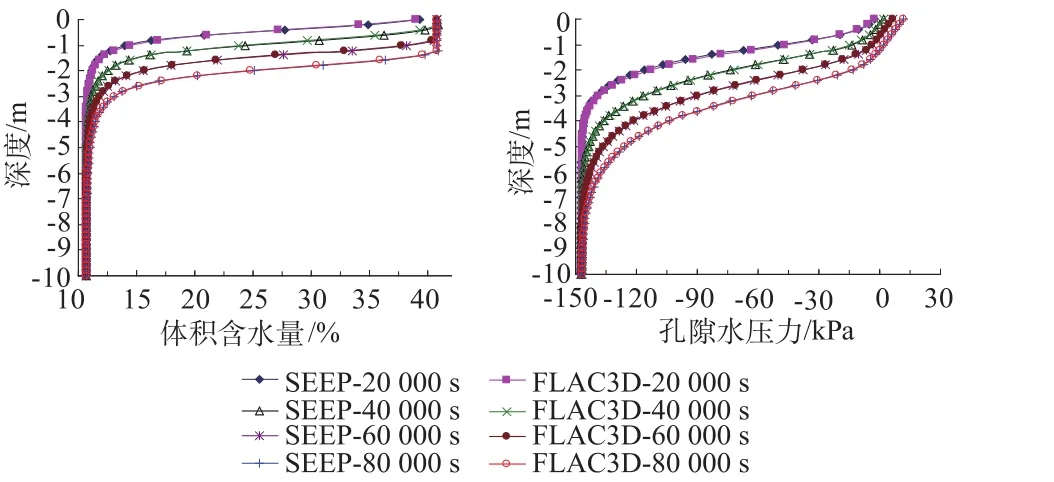
图5 q为2ksat条件下的体积含水量和孔隙水压力随深度的分布曲线Fig．5 Distributions of volumetric water content and pore-water pressure w ith depth（q＝2ksat）

模拟结果表明：

（1）饱和一维入渗条件下，在浸润前锋附近，土体含水量由近饱和状态迅速降低（图3）。数值模拟结果与Lumb［9］的现场观测和分析解呈现的规律一致。

表3 流固耦合计算中所用力学参数Table 3 Mechanical parameters adopted in the fluid-mechanical coupled analysis

（2）当入渗速度小于饱和渗透系数时，其浸润区仅损失部分负孔隙水压力。在浸润前锋，含水量亦迅速降低（图4）。

（3）如图5所示，在边界条件q＝2ksat下，2个程序的模拟结果也较为相符，孔隙水压力由正值平滑降为负值。该结果说明修正后该渗流模型从饱和到非饱和入渗过渡良好。

（4）体积含水量与孔隙水压力在浸润区前缘的降低速度受所采用的土水特征曲线和渗透系数曲线影响（图3—图5）。其影响程度应进一步参照试验数据进行深入研究。

5 扩展应用

在实现渗流计算的基础上，可进一步利用FLAC3D进行流固耦合分析。对于非饱和土，Bishop［15］将太沙基的饱和土有效应力公式做如下扩展，即

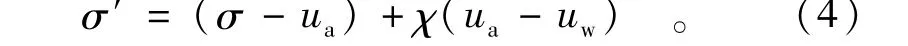
式中：χ为与饱和度s有关的参数（作为简化，可取χ＝s）；ua为孔隙气压力。

利用公式（4）修正FLAC3D中的总应力与有效应力的关系后，将可在程序中描述非饱和土的应力应变关系。需注意的是，孔隙气压力ua与孔隙水压力相关联，非饱和土ua＝0，饱和土ua＝uw。非饱和土的摩尔－库仑强度公式可表示［15］为

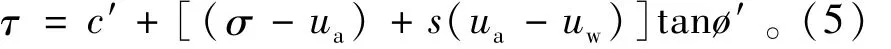
式中c′和ø′分别为有效黏聚力和有效内摩擦角。

结合前面对FLAC3D渗流模型的扩展，非饱和土有效应力公式（4），强度公式（5），以及比奥固结理论［16］，即可利用FLAC3D内置的耦合模型进行非饱和土流固耦合分析（弱耦合）。

运用该方法，笔者模拟了灌溉水沿黄土裂缝入渗导致的土体破坏过程［14］，包括裂缝中水位上升、维持、下降和消散的过程（表2）。限于篇幅，这里仅选取灌溉水完全沿裂缝入渗的典型算例简要介绍如下。计算网格见图6（a），所选渗流参数及力学参数见表1、表3。当裂缝中水位降低到裂缝底部后，其孔压场、位移场及塑性区的最终累计量如图6（b）和图6（c）所示（对称条件下仅取左部分）。可以看出：浸润区向深部发展，部分土体单元达到了塑性状态，且土体沿裂缝临空面向外移动。数值模拟结果反映了现场灌水时土体中渗流、变形破坏的趋势，取得了较好的应用效果。

表2 裂缝参数及灌溉模拟过程Table 2 The param eters of the crack and the simulated processes of irrigation

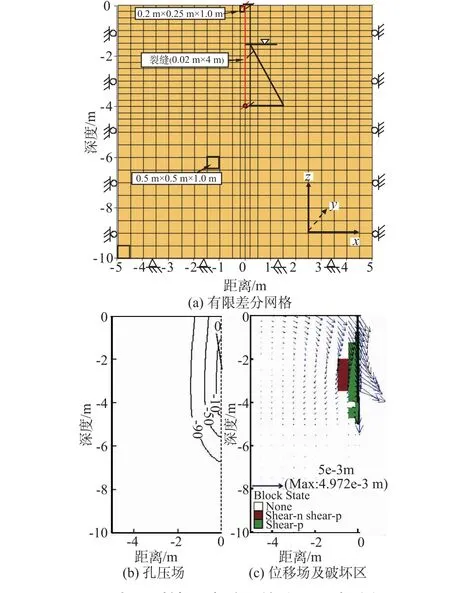
图6 水沿裂缝入渗过程的流固耦合分析图Fig．6 Fluid-mechanical coupled analysis of soil failure along the crack subjected to water infiltration

6 结 语

本文利用FLAC3D内置的FISH语言，对其渗流模型进行了扩展。文中所述内容概括如下：

（1）将实验室测得的原状黄土土水特征曲线，利用MATLAB实现了参数拟合。根据拟合结果，该黄土残余含水量为8．7%，饱和含水量为40．7%。

（2）在FLAC3D中，将拟合参数编写为子程序，并在渗流分析时迭代调用，可实现非饱和土的渗流模拟。运用该方法模拟了不同边界条件下的一维入渗过程。验证表明，该方法准确。

（3）模拟结果显示，在浸润前锋附近，土体含水量由近饱和状态迅速降低。模拟结果与前人的现场观测和分析解呈现的规律一致。

（4）基于以上非饱和渗流模型，FLAC3D的流固耦合模块可进一步扩展应用于非饱和土流固耦合分析。本文的研究成果对研究非饱和土理论，及扩展FLAC3D在非饱和土数值计算方面均具有一定意义。

［1］ 毛昶熙．渗流计算分析与控制［M］．北京：中国水利水电出版社，2003：1－2．（MAO Chang-xi．Seepage Computation and Analysis and Control［M］．Beijing：China Water Power Press，2003：1－2．（in Chinese））

［2］ NG CWW，SHIQ A．Numerical Investigation of the Stability of Unsaturated Soil Slopes Subjected to Transient Seepage［J］．Computers and Geotechnics，1998，22（1）：1－28．

［3］ 王铁行．非饱和黄土路基水分场的数值分析［J］．岩土工程学报，2008，30（1）：41－45．（WANG Tie-hang．Moisture Migration in Unsaturated Loess Subgrade［J］．Chinese Journal of Geotechnical Engineering，2008，30（1）：41－45．（in Chinese））

［4］ YOO C，KIM SB．Three-Dimensional Numerical Investigation of Multifaced Tunneling in Water-Bearing Soft Ground［J］．Canadian Geotechnical Journal，2008，45（10）：1467－1486．

［5］ ITASCA．FLAC 3D Version 2．61 User’s Guide［K］．Minneapolis，Minnesota，USA：ITASCA Inc．，2002．

［6］ 李 毅，伍 嘉，李 坤．基于FLAC3D的饱和-非饱和渗流分析［J］．岩土力学，2012，33（2）：617－622．（LIYi，WU Jia，LIKun．Saturated-Unsaturated Seepage Analysis Based on FLAC3D［J］．Rock and Soil Mechanics，2012，33（2）：617－622．（in Chinese））

［7］ RICHARDSR A．Capillary Conduction of Liquid Through Porous Mediums［J］．Physics，1931，1（5）：318－333．

［8］ PHILIP JR．The Theory of Infiltration 1：The Infiltration Equation and Its Solution［J］．Soil Science，1957，83（5）：345－358．

［9］ LUMB P．Effect of Rainstorms on Slope Stability［M］．Hong Kong：Hong Kong Joint Group of the Institutions of Civil，Mechanical and Electrical Engineers，1962．

［10］FREDLUND D G，RAHARDJO H．Soil Mechanics for Unsaturated Soil［M］．US：Wiley，1993．

［11］LEONG EC，RAHARDJO H．Review of Soil-Water Characteristic Curve Equations［J］．Journal of Geotechnical and Geoenvironmental Engineering，1997，123（12）：1106－1117．

［12］ZHOU Y D，CHEUK CY，THAM LG．NumericalModelling of Soil Nails in Loose Fill Slope under Surcharge Loading［J］．Computers and Geotechnics，2009，36：837－850．

［13］李志清，李 涛，胡瑞林，等．非饱和土土水特征曲线（SWCC）测试与预测［J］．工程地质学报，2007，15（5）：700－707．（LI Zhi-qing，LI Tao，HU Rui-lin，et al．Methods for Testing and Predicting of SWCC in Unsaturated Soil Mechanics［J］．Journal of Engineering Geology，2007，15（5）：700－707．（in Chinese））

［14］ZHOU Y F．Study on Landslide in Loess Slope Due to Infiltration［D］．Hong Kong：The University of Hong Kong，2012．

［15］BISHOP A W．The Principle of Effective Stress［J］．Teknisk Ukeblad，1959，106（39）：859－863．

［16］李广信．高等土力学［M］．北京：清华大学出版社，2006．（LIGuang-xin．Advanced SoilMechanics［M］．Beijing：Tsinghua University Press，2006．（in Chinese） ）

（编辑：姜小兰）

Imp lementation and Verification of Unsaturated Seepage Analysis in FLAC3D

ZHOU Yue-feng1，2，THAM L G2，YANW M2，FAN Shao-peng2，3
（1．Key Laboratory of Geotechnical Mechanics and Engineering of Ministry ofWater Resources，Yangtze River Scientific Research Institute，Wuhan 430010，China；2．Department of Civil Engineering，The University of Hong Kong，Hong Kong，China；3．Hydraulic Design Department，Changjiang Institute of Survey，Planning，Design and Research，Wuhan 430010，China）

The seepagemodel in FLAC3D was extended using its in-built programming language FISH．The SWCC（SoilWater Characteristic Curve）for seepage in unsaturated loess was best-fitted using MATLAB．The obtained parameterswere written as a subroutine and invoked in each step in the seepagemodel of FLAC3D to simulate the unsaturated loess．One-dimensional infiltration problem in three boundary conditionswasmodeled using both the finite differencemethod and the finite elementmethod to verify the extension in FLAC3D．The comparison results show that the abovemethod is appropriate．The findings of this paper aremeaningful in the investigation of the unsaturated soil theory and in the application of FLAC3D to simulate unsaturated soil problems．

unsaturated soil；seepage；SWCC；FLAC3D；redevelopment

TV139．1

A

1001－5485（2013）02－0057－05

10．3969／j．issn．1001－5485．2013．02．012

2012－10－11；

2012－11－22

香港研究资助局资助项目（HKU7140／08E）

周跃峰（1982－），男，山西侯马人，工程师，博士，主要从事黄土滑坡机理研究与岩土工程数值计算研究，（电话）13971606626（电子信箱）zhouyuefenghku＠gmail．com。