对自相似扩展（SSE）模型的改进和研究

王晶晶，罗冰显，刘四清，龚建村

1 中国科学院空间科学与应用研究中心，北京 100190

2 中国科学院空间天气学国家重点实验室，北京 100190

1 引 言

日冕物质抛射（Coronal Mass Ejection，CME）可能起源于太阳上的活动区域（Active Region，AR）和暗条爆发，有时还伴随着耀斑的发生［1－3］，在行星际空间中传播的一部分CME被认为是具有通量绳结构的磁云（Magnetic Cloud，MC），在磁云内部，磁场分量平滑地转变方向，磁压比气体压强高［4］.

SOHO（SOlar and Heliospheric Observation）［5］的日冕仪（Large Angle Spectrometric Coronagraph，LASCO）［6］观测了CME在30个太阳半径内的区域中传播的过程.被SOHO／LASCO观测到投影观测张角达到360°的是全晕（halo）CME，这类CME通常会以很高的速度传播到达地球、并引发较大的地磁暴［7－8］.锥模型［9－13］是目前在国际上应用很广泛的CME模型之一，不但可以应用于全晕CME、偏晕（partial halo）CME，也能应用于非全晕（non-halo）CME的分析.利用锥模型对SOHO／LASCO观测的CME图像进行拟合，尤其是对CME最明亮“前沿”的观测，可以得到CME的一些基本参数，如CME的源区、主传播方向、角宽度和传播速度等.这些CME参数对于预报CME是否能够到达地球、何时到达地球具有非常重要的参考意义.

CME的角宽度包括纬度方向的角宽度和经度方向的角宽度［8，14］.基于锥模型等 CME 模型和SOHO／LASCO等仪器对CME的图像观测，CME角宽度的分布特征已被多次研究过，如Michalek等使用锥模型研究了朝向地球传播的325个CME事件，这些CME在SOHO／LASCO图像观测可能呈现全晕和偏晕CME形态，得到CME的平均角宽度是85°［10］；Xue等使用冰淇淋模型研究了 2000—2002年共40个CME事件，这些CME角宽度的最大值和最小值分别是179°和36.8°，平均角宽度是114°，径向传播速度平均值是1104km·s－1［11］；St.Cyr等研究了SOHO／LASCO于1996至1998年观测到的、共841个CME事件的统计特征，这些CME角宽度的平均值和中位数分别是72°和50°，径向传播速度平均值是549km·s－1［12］；在这项研究的基础上，Yeh等使用锥模型矫正了观测CME的投影误差，得到的CME角宽度的平均值由72°减小为59°，径向传播速度的平均值由549km·s－1增大为792km·s－1［13］.

STEREO 卫 星 （Solar-TErrestrial RElations Observatory）［15］拓展了CME在行星际空间中传播的可观测区域.STEREO卫星包括STEREO-Ahead（STA）和STEREO-Behind（STB）两颗卫星，其搭载的行星际成像仪（Heliospheric Image，HI）［16］将对日地连线附近区域的遥感图像观测距离扩展到12～318个太阳半径的范围.在超过20个太阳半径之外，CME被认为是速度平缓地在行星际空间中传播，因此在HI观测范围内的CME可以被认为是速度平缓地在行星际空间中传播［17］.

由于视角和观测范围非常广阔，基于STEREO／HI的图像提取CME参数的方法与基于SOHO／LASCO图像的方法不同 .使 用J-map方 法［18－19］处理STEREO／HI的图像得到延伸角－时间图（elongation-time plot，J-map图像）后，就可以从J-map图上提取出随时间变化的CME的运动轨迹.基于单颗STEREO／HI图像提取CME参数的方法包括固定 Φ角拟合法（Fixed-Φ，FΦ）［20］和调和均值拟 合 法 （Harmonic-mean，HM）［21］，可 以 提 取 的CME参数包括CME的主传播方向和传播速度.其中，FΦ拟合法假设CME是固定方向传播的小质点，HM拟合法假设CME为一端固定于日心、沿径向向外传播的球形前沿的通量绳结构.此后，Lugaz等提出了自相似扩展拟合法（Self-Similar Expansion，SSE）［17，22－23］，假设 CME是具有恒定角宽度、沿径向向外传播的自相似球形前沿（如图1所示，半角宽度由λ表示），CME角宽度的取值范围被限制在FΦ（半角宽度为0°）和 HM（半角宽度为90°）模型之间，可以提取的CME参数包括CME的主传播方向、传播速度和角宽度，其中拟合角宽度可以用以区分在经度方向上角宽度差异明显的太阳风高速流和CME，但拟合的不确定性也随着模型未知参数自由度的增加而增大.

图1 延伸角和CME主传播方向示意图CME前沿由红色实线标出的半圆形表示，它是由黑色实线标出的CME前沿自相似扩展而成的.点O、A、B和E分别表示太阳、STA卫星、STB卫星和地球的位置，T为CME前沿中心点.αA和αB分别表示T相对STA、STB的延伸角；βA和βB分别表示OT与OA和OB的夹角，β0表示OT与OE的夹角，βA、βB和β0代表了在某一位置角上CME相对于STA、STB和地球的传播方向（逆时针方向为正）；TA和TB分别是STA和STB卫星相对CME前沿的切点位置；λ和ω分别代表了CME的半角宽度和半圆锥角.Fig.1 Illustration of elongation and propagation direction of the CMEIn this figure，the semicircle marked by red solid line is the CME front，which is developed by self-similar expansion from the semicircle marked by black solid line.The Sun，STA，STB and the Earth was noted as O，A，B and E，respectively.T is the center of the CME front.αAandαBare elongation angle of T observed by STA and STB，respectively.Propagation direction of CME observed by STA，STB and Earth areβA，βBandβ0，which are the separation between STA，STB，Earth and OT，respectively（positive number is in the direction of counterclockwise）.TAand TBare the tangent points of STA and STB relative to CME leading edge（the circle in Fig b）modeled by SSE.λis the half-angular width of the CME.ωis the half-cone angle.

由于HI的视野范围有限，而且从平面内任一点观测球形前沿，看到的最大展宽就是球形前沿的直径长度，所以本文只关注球形前沿的前半球.考虑到CME前沿形态和角宽度可能并不局限于FΦ和HM模型假设的范围之间，甚至可能会出现CME球形前沿的球心到太阳的距离小于球半径的情况，为了能描述更多种CME前沿的特征，本文在SSE模型的基础上作了修改，利用由日心出发的、圆锥截面过球心的圆锥来描述这种圆锥角恒定自相似扩展的半球形前沿，用半圆锥角ω代替半角宽度λ，取值范围是［0°，90°］，本文称为修改后的自相似扩展（Modified-SSE，MSSE）模型.

本文利用2010年STEREO卫星HI图像提取出的23个CME在太阳赤道平面上的运动轨迹，使用FΦ、HM、SSE和MSSE拟合法提取CME参数；也通过与STEREO和ACE卫星实测ICME参数的对比和统计，讨论了FΦ、HM、SSE和MSSE这四种CME参数提取方法用于CME事件预报的优劣.

2 CME事件选取和CME参数的提取方法

2.1 CME事件的选取

在2010年，太阳-STEREO卫星的连线与日地连线的夹角由65°逐渐增大至约90°，对于朝向地球传播的CME事件，STA和STB卫星正好能从侧面观测到，STA和STB卫星对CME的投影观测张角与CME的实际角宽度差异较小；对于朝向STA或STB卫星传播的CME事件，STA和STB卫星对CME的投影观测张角可能超过180°，与CME的实际角宽度差异较大.由于STEREO卫星和地球都在太阳赤道平面附近，我们根据位置角为90°的J-map图，提取出CME事件在行星际空间中的运动轨迹.

图2a是4月3—5日STA／HI观测到的在太阳赤道平面的J-map图像，图2b中三角符号代表从图2a中提取的朝向地球传播的、于04／05到达了ACE卫星的CME实测运动轨迹（time-elongation profile），实线代表的是使用MSSE拟合法拟合的运动轨迹.

为了能在超过1天的时间范围内分析CME在行星际空间中传播的特征，我们选出了2010年在STEREO／HI图像数据中被观测的延伸角（elongation）最大值超过30°的CME事件，并进一步分析这些CME事件在太阳赤道平面附近的CME参数，如主传播方向、传播速度和角宽度.

本文利用2010年ACE卫星对行星际磁场和太阳风等离子体的实测数据，找出到达地球的实测ICME事件，同时利用STEREO卫星的实测ICME事件列表（到达STEREO卫星的ICME列表来自http：∥www-ssc.igpp.ucla.edu／forms／stereo／stereo＿level＿3.html［2012-06-06］），结合 STEREO／HI观测到的CME事件，筛选出HI图像观测和实地ICME观测一一对应的CME事件进行深入分析.其中，STA／HI观测到的CME事件有13个，STB／HI观测到的CME事件有10个.

2.2 基于单颗卫星HI观测的CME参数提取方法

2.2.1 自相似扩展拟合法（SSE）

考虑到CME具有三维结构，当其在超过20个太阳半径的行星际空间中传播时，主传播方向和角宽度恒定，“前沿”中心点沿径向匀速传播.自相似扩展拟合法（SSE）假设CME具有恒定角宽度、沿径向向外传播的自相似球形前沿，这个前沿在图1中由圆心在C点的红色圆形标出，它是由前一时刻的黑色圆形前沿自相似扩展而来的，Lugaz利用由日心出发的、与这个球形前沿相切的圆锥，来描述这种圆锥角恒定自相似扩展的特征，此时，球形前沿的半径为圆锥的高h与半圆锥角（图1中所示的λ）的正弦函数的乘积 （h·sinλ），这个圆锥角（2λ）就是通常所说的CME角宽度.

SSE拟合法也假设CME前沿在HI观测范围内速度变化很小，可以看做是以恒定速度传播，而且卫星观测点到CME“前沿”上“被观测部分”的连线与这个球形“前沿”相切.Lugaz用CME的主传播方向βA、传播速度V和半角宽度λ作为SSE模型的三个未知参数，其中，主传播方向βA和传播速度V描述了球形前沿的传播朝向和位置，而恒定的半角宽度λ是与球形前沿相切的圆锥的基本参数，也制约了自相似扩展的球形前沿可能扫过的范围.

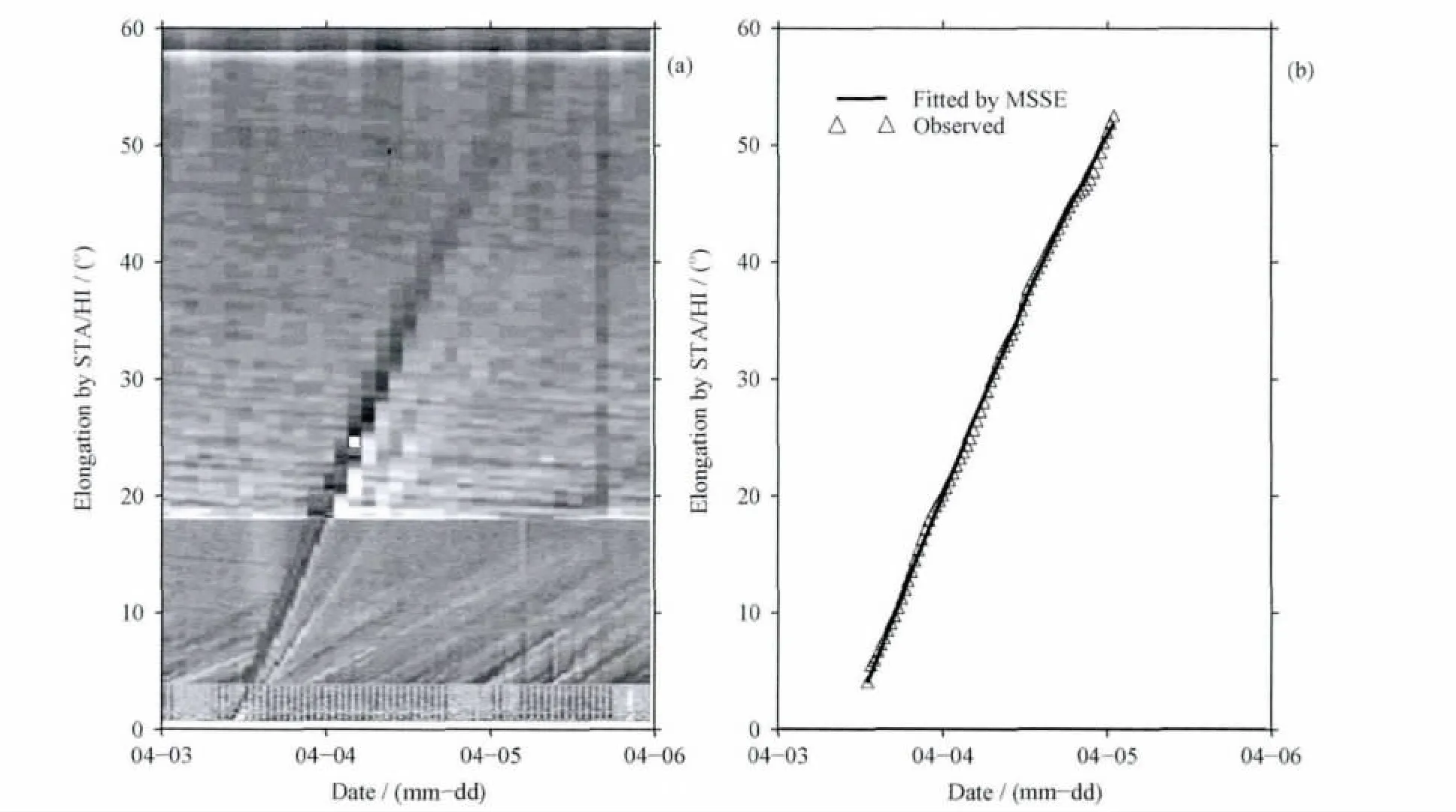
图2 04／05CME事件J-map图纵轴elongation是在太阳赤道平面上，STA／HI对CME的观测延伸角，横轴是日期.Fig.2 J-map of 04／05CMEIn this figure，the horizontal axis represents CME elongation observed by STA／HI in the solar equatorial plane.The vertical axis represents date.

图1是太阳赤道平面上SSE模型的示意图，C是CME前沿的圆心，T是CME主传播方向上的CME前沿中心点，STA和STB卫星对这个圆形前沿的实际观测点分别是TA和TB点，即卫星对CME前沿的观测视线与圆的切点，此时CME主传播方向上“真实前沿”T的日心距dT表达式如下：

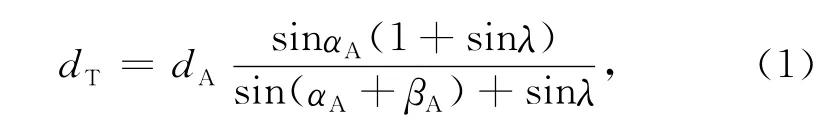
其中，αA是STA的观测延伸角，dA是STA的日心距，βA是STA到日心的连线与太阳到T的连线之间的夹角.后文中CME的主传播方向由CME主传播方向与日地连线（OE）的夹角β0表示，偏向东（图1中以太阳为圆心的逆时针方向）为正值，偏向西（图1中以太阳为圆心的顺时针方向）则为负值.

只使用单颗卫星的HI观测数据时，SSE拟合法基于公式（1）的假设，对某一时刻HI图像上的CME前沿观测延伸角αA的计算公式如下：

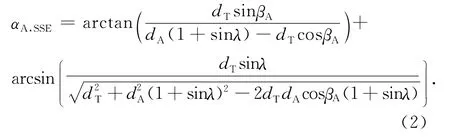
假设CME的半角宽度λ、主传播方向βA和在主传播方向上的传播速度V恒定，分别可能在区间［0°，90°］、区间［－80°，230°］和区间［200km·s－1，1600km·s－1］内以1°或1km·s－1为间隔取任意值，比较根据公式（2）计算的理论延伸角αtheoretical，SSE与实测延伸角αobserved，根据最小误差原则，将二者的绝对差异最小值σα＝min（σα）对应的CME参数作为最优拟合参数——半角宽度λ、主传播方向β0，SSE和传播速度VSSE，并将二者的绝对差异不超过2min（σα）的CME参数最大范围作为这个CME参数的拟合误差值.

Lugaz的SSE拟合法假设CME角宽度（2λ）是在［0°，180°］范围内取值的未知参数，当半角宽度λ取最小值0°时，CME可以看做是固定方向传播的小质点，也就是固定Φ角拟合法（FΦ）对CME前沿形态的假设；当半角宽度λ取最大值90°时，代表CME的球形前沿一端固定于日心、沿径向向外传播，也就是调和均值拟合法（HM）对CME前沿形态的假设；FΦ和HM模型分别是SSE模型的一种特殊情况，它们对CME前沿形态和角宽度的固定假设，在SSE模型中都能得到体现.

2.2.2 修改后的SSE模型（MSSE）

考虑到CME前沿形态和角宽度可能并不局限于FΦ和HM模型假设的范围之间，甚至可能会出现CME球形前沿的球心到太阳的距离小于球半径的情况，那么使用SSE拟合法时仍然将半角宽度λ放在［0°，90°］范围内取值，就可能会造成提取的CME参数与实际CME参数的较大误差.但在原SSE模型中，球形前沿的半径等于圆锥的高h与半圆锥角λ的正弦函数的乘积（h·sinλ），正弦函数存在周期性，当半圆锥角λ超过90°时，圆锥角超过180°圆锥的开口将反向.

由于HI的视野范围有限，而且从平面内任一点观测球形前沿，看到的最大展宽就是球形前沿的直径长度，所以本文只关注球形前沿的前半球.同时，也为了能让SSE模型描述更多种CME前沿的特征，本文将SSE模型的假设作了如下修改：

（1）CME的前沿是半球（如图1中由圆心在C点的红色实线半圆标出），由前一时刻的黑色实线半圆形前沿自相似扩展而来的.

（2）本文利用由日心出发的、圆锥截面过球心的圆锥（见图1中由蓝色虚线标出的圆锥），来描述这种圆锥角恒定自相似扩展的特征，此时，球形前沿的半径为圆锥的高h与半圆锥角（图1中所示的ω）的正切函数的乘积 （h·tanω）.

（3）修改后的SSE模型（Modified-SSE，MSSE）的三个未知参数中，用半圆锥角ω代替半角宽度λ，取值范围是［0°，90°］.

MSSE模型中，恒定的半圆锥角ω不但描述了半球形前沿自相似扩展的特征，也制约了半球形前沿可能扫过的范围，也就是这个CME半球形前沿的半角宽度，为了与SSE模型中的半角宽度λ区分，后文中使用半圆锥角ω指代半球形CME前沿的半角宽度.图3是SSE模型角宽度取值范围的变化示意图，图3a是Lugaz提出的SSE模型，半角宽度λ由0°逐渐增大至最大值90°，图3b是MSSE模型，半圆锥角ω由0°逐渐增大至最大值90°.

当 MSSE模型中半圆锥角ω在［0°，45°］范围内取值时，总能找到SSE模型中在［0°，90°］范围内取值的半角宽度λ与之一一对应，使得CME的前沿具有相同的球半径，满足sinλ＝tanω.例如，FΦ拟合法假设CME是固定方向传播的小质点，对应半角宽度λ和半圆锥角ω都取最小值0°的情况；HM拟合法假设CME的球形前沿一端固定于日心、沿径向向外传播，对应半角宽度λ和半圆锥角ω分别取90°和45°的情况（见图3）.可见，MSSE模型仍然能描述所有在SSE模型中能得到体现的CME前沿形态，但当球半径相同时，MSSE模型中半圆锥角ω显然比SSE模型中半角宽度要小.

图3 SSE模型角宽度取值范围的变化示意图（a）Lugaz提出的SSE模型，半角宽度λ由0°逐渐增大至最大值90°；（b）MSSE模型，半圆锥角ω由0°逐渐增大至最大值90°.Fig.3 Illustration of SSE model with the different ranges of the angular width（a）SSE model prompted by Lugaz，with half-angular width，λ，ranging from 0°to 90°；（b）MSSE model，with half-cone angle，ω，ranging from 0°to 90°.

当 MSSE模型中半圆锥角ω 在［45°，90°］范围内取值时，MSSE模型所描述的CME前沿形态，在SSE模型中是体现不出来的.例如，当半圆锥角ω取最大值90°时，CME可以看做是球心在日心、沿径向向外传播的半球形（见图3b）.本文将SSE模型中球形前沿的假设修改为半球形前沿，能够避免一部分前沿背向主传播方向传播的情况出现.

由于MSSE模型将CME的主传播方向βA、传播速度V和半圆锥角ω作为未知参数，CME主传播方向上“真实前沿”T的日心距dT表达式（1）和观测延伸角的计算公式（2）也应作出对应的修改，如下：

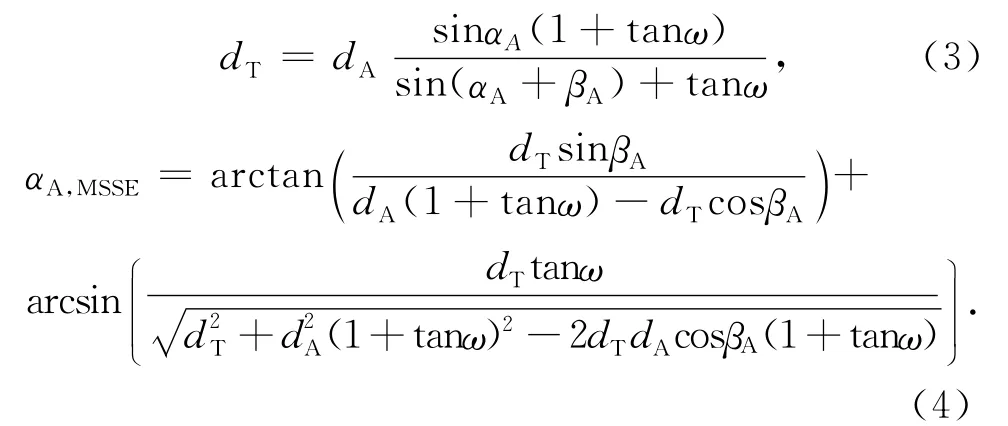
利用MSSE拟合法，本文将半圆锥角ω作为判断CME是否能够到达、何时到达某颗卫星（本文中分析了STA、STB和ACE三颗卫星）的重要参数.除了MSSE拟合法，本文也使用了FΦ、HM、SSE拟合法提取CME参数，并将半角宽度λ作为判断CME是否能够到达、何时到达某颗卫星的重要参数.

对比根据这四种方法提取的CME参数预报CME的差异，以ACE卫星为例，当使用FΦ和HM拟合法时，如果半角宽度λ分别为40°和90°的CME前沿能够扫过ACE卫星（CME主传播方向与太阳－ACE卫星连线的夹角分别不超过40°和90°），就认为这个CME有可能到达ACE卫星，并将计算得到的CME前沿扫过ACE卫星的时间作为预计到达时间Tarrival，FΦ和Tarrival，HM；当使用 MSSE 拟合法时，如果半圆锥角为ω的CME前沿能够扫过ACE卫星（CME主传播方向与太阳-ACE卫星连线的夹角≤ω），就认为这个CME有可能到达ACE卫星，并将计算得到CME前沿扫过ACE卫星的时间作为预计到达时间Tarrival，MSSE.

当使用SSE拟合法拟合得到的CME球形前沿与使用MSSE拟合法拟合得到的CME半球形前沿部分重合时，利用SSE拟合法预报CME事件可能扫过［β0－λ，β0＋λ］的角宽度范围，而利用 MSSE拟合法预报CME事件只可能扫过［β0－ω，β0＋ω］的角宽度范围，考虑到ω＜λ，MSSE模型将CME前沿假设为半球形，当一颗卫星位于［β0－λ，β0－ω］或［β0＋ω，β0＋λ］的角宽度范围内，相比SSE拟合法对CME是否能扫过这颗卫星的预报结果，MSSE拟合法会造成预报结果被低估.

2.2.3 MSSE模型的特点

图4是基于MSSE模型，以恒定的速度500km·s－1传播的、主传播方向与HI观测卫星之间的夹角自－30°至210°以30°为间隔变化时CME前沿在J－map上的运动轨迹，七条不同的曲线分别代表了半圆锥角ω自0°至90°以15°为间隔变化时CME前沿在J－map上的运动轨迹.可以看出，对于主传播方向和传播速度相同的CME，半圆锥角ω越大，在J－map上传播得越快；当主传播方向与HI观测卫星之间的夹角在30°至90°之间变化时，不相同的半圆锥角ω对应的CME前沿运动轨迹在观测延伸角不超过30°的范围内差异都很小.可是当观测延伸角比较大时对CME前沿的观测数据并不容易得到，这种情况限制了MSSE拟合法的应用范围，也可能出现在CME的主传播方向与HI观测卫星之间的夹角在30°至90°之间变化时，使用MSSE拟合法得到的CME拟合参数与实际CME参数差异较大的现象.

图5是基于MSSE模型，以恒定的速度500km·s－1传播的、半圆锥角ω自0°至90°以15°为间隔变化时CME前沿在J－map上的运动轨迹，七条不同的曲线分别代表了主传播方向与HI观测卫星之间的夹角自0°至180°以30°为间隔变化时CME前沿在J－map上的运动轨迹.可以看出，对于角宽度和传播速度相同的CME，刚开始传播时，由实线代表的CME的主传播方向与HI观测卫星之间的夹角为90°的CME在J－map上传播得最快，但在这之后逐渐被夹角更小的CME超过；当半圆锥角ω超过75°时，主传播方向与HI观测卫星之间的夹角并不相同的CME前沿运动轨迹差异很小.因此，当使用MSSE拟合法提取的CME拟合角宽度参数超过75°时，可能出现拟合参数与实际CME参数差异较大的现象.

结合图4和图5，我们认为半圆锥角ω的取值范围［0°，90°］能够更全面地描述 MSSE模型参数对J－map上CME前沿运动轨迹的变化特点.当CME符合MSSE模型的假设时，我们认为当半圆锥角ω不超过75°、且主传播方向与HI观测卫星之间的夹角小于30°或大于90°时，使用MSSE拟合法可以得到与实际CME参数符合较好的拟合参数值.上文介绍了提取CME参数的FΦ、HM、SSE和MSSE拟合法.下文将对MSSE拟合法提取的CME参数作进一步的统计分析，并将其与ICME事例的实测参数进行对比，讨论模型中CME前沿形态的假设对CME事件预报的影响.

图4 MSSE模型下在J-map上随着主传播方向变化的CME前沿的运动轨迹CME以恒定速度500km·s－1传播，主传播方向与HI观测卫星之间的夹角βA自－30°至210°以30°为间隔变化，分别对应图中在时间轴上的起点间隔50h的9组曲线，固定主传播方向的每组曲线包含半圆锥角ω自0°至90°以15°为间隔变化的7条曲线.Fig.4 Profiles of leading edge on J-map for MSSE model corresponding to CME propagation directionIn this figure，CME propagates at a constant radial speed of 500km·s－1.Each pair of 9pairs of profiles corresponds to separation angles between propagation direction and line of sight for HI，βA，ranging from －30°to 210°in increments of 30°.Each pair of profiles is offset from the previous one by 50hour for clarity.Each set of 7profiles inside pairs of profiles corresponds to half-cone angle，ω，ranging from 0°to 90°in increments of 15°.

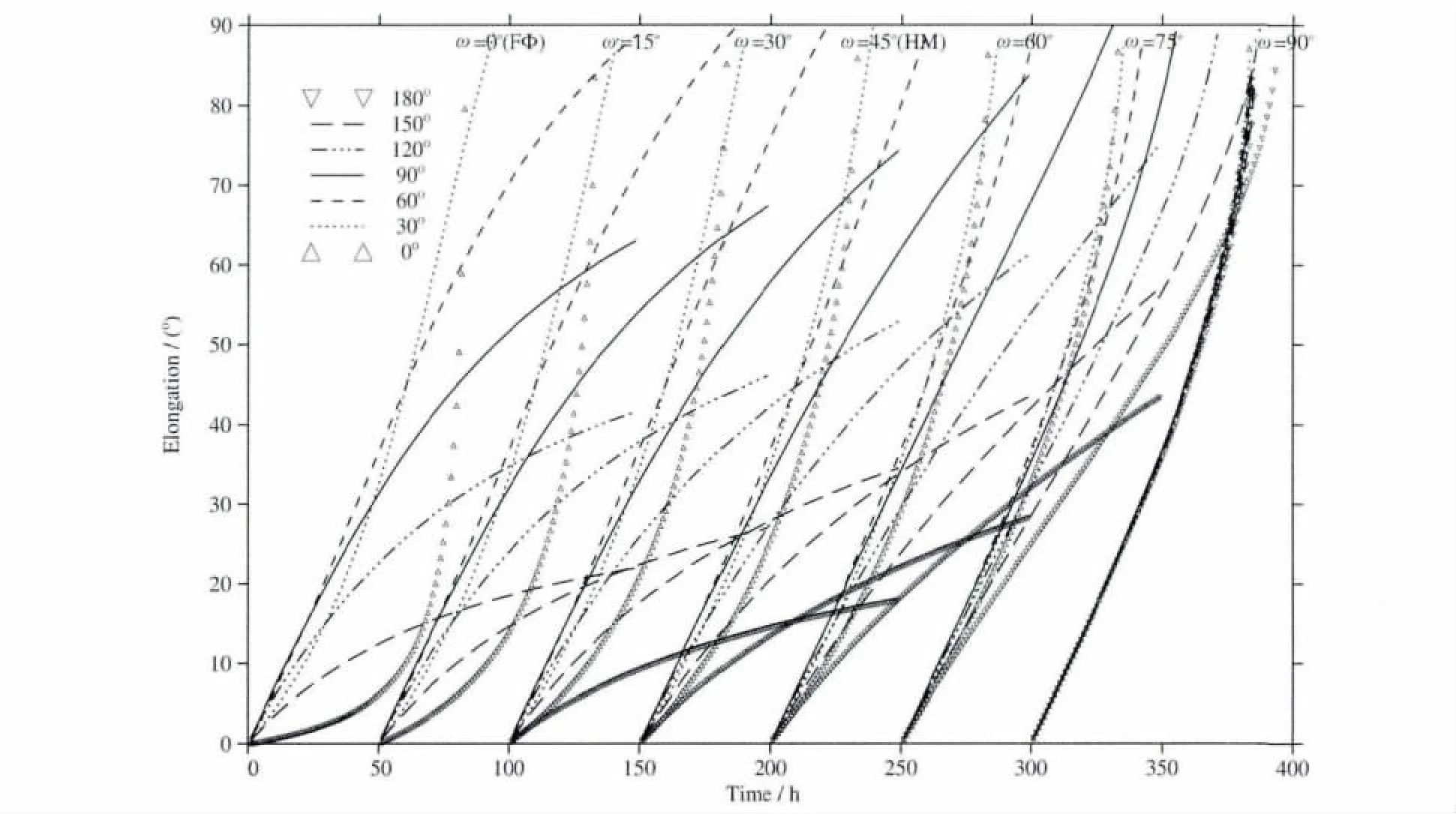
图5 MSSE模型下在J-map上随着半圆锥角变化的CME前沿的运动轨迹CME以恒定速度500km·s－1传播，半圆锥角ω自0°至90°以15°为间隔变化，分别对应图中在时间轴上的起点间隔50小时的7组曲线，半圆锥角ω相同的每组曲线包含主传播方向与HI观测卫星之间的夹角βA自0°至180°以30°为间隔变化的7条曲线.Fig.5 Profiles of leading edge on J-map for MSSE model corresponding to CME angular widthIn this figure，CME propagates at a constant radial speed of 500km·s－1.Each pair of 7pairs of profiles corresponds to half-cone angle，ω，ranging from 0°to 90°in increments of 15°.Each pair of profiles is offset from the previous one by 50hour for clarity.Each set of 7 profiles inside pairs of profiles corresponds to separation angles between propagation direction and line of sight for HI，βA，ranging from 0°to 180°in increments of 30°.

3 CME参数提取结果的对比分析

3.1 预报误差统计分析

本文使用FΦ、HM、SSE和MSSE拟合法分析了STA／HI观测到的13个CME事件和STB／HI观测到的10个CME事件.需要注意的是，当使用MSSE拟合法提取的CME半圆锥角超过45°时，使用SSE拟合法提取的CME半角宽度达到最大值90°，也就是说，在这些事件中，SSE拟合法提取的CME参数与HM拟合法提取的CME参数相同；而在其他事件中，使用MSSE和SSE拟合法提取的CME主传播方向和传播速度是相同的.

图6是这23个CME事件使用FΦ、HM和MSSE拟合法提取CME参数的统计分析图.观察图6（a—c），可见MSSE拟合法得到的CME主传播方向分布范围最大、最分散，FΦ拟合法得到的CME主传播方向分布范围最小、最集中；观察图6（d—e）可以看到，使用FΦ和HM拟合法提取CME主传播方向线性相关性很强，除了STA／HI和STB／HI分别观测到的3个、1个CME事件外，HM和MSSE拟合法提取CME主传播方向线性相关性也很强；观察图6（f—g）可以看到，使用FΦ和HM拟合法、使用HM和MSSE拟合法提取CME主传播方向上的传播速度的线性相关性分别较强和较弱.

表1列出了本文研究的23个CME事件的实测到达时间、HI图像和实测ICME的观测卫星，以及根据这四种方法提取的CME参数分析的预报结果与实测ICME的误差.其中，｜ΔβSC｜是CME主传播方向与太阳－实测ICME的卫星连线之间的夹角，｜ΔTarrival｜是预计到达时间误差.其中，预计到达时间误差是预计到达时间和实测ICME起始时间（通量绳结构出现的时间）之间的差异.编号10—15的事件使用FΦ拟合法分析的预计到达卫星与实测ICME事件的卫星不符合，所以在表格中对应的预计到达时间误差未填入数据；编号11—13、15的事件使用HM和SSE拟合法分析的预计到达卫星与实测ICME事件的卫星符合，但预计到达时间误差太大（数据用黑斜体标记），所以在计算预计到达时间误差的平均值时未列入计算.

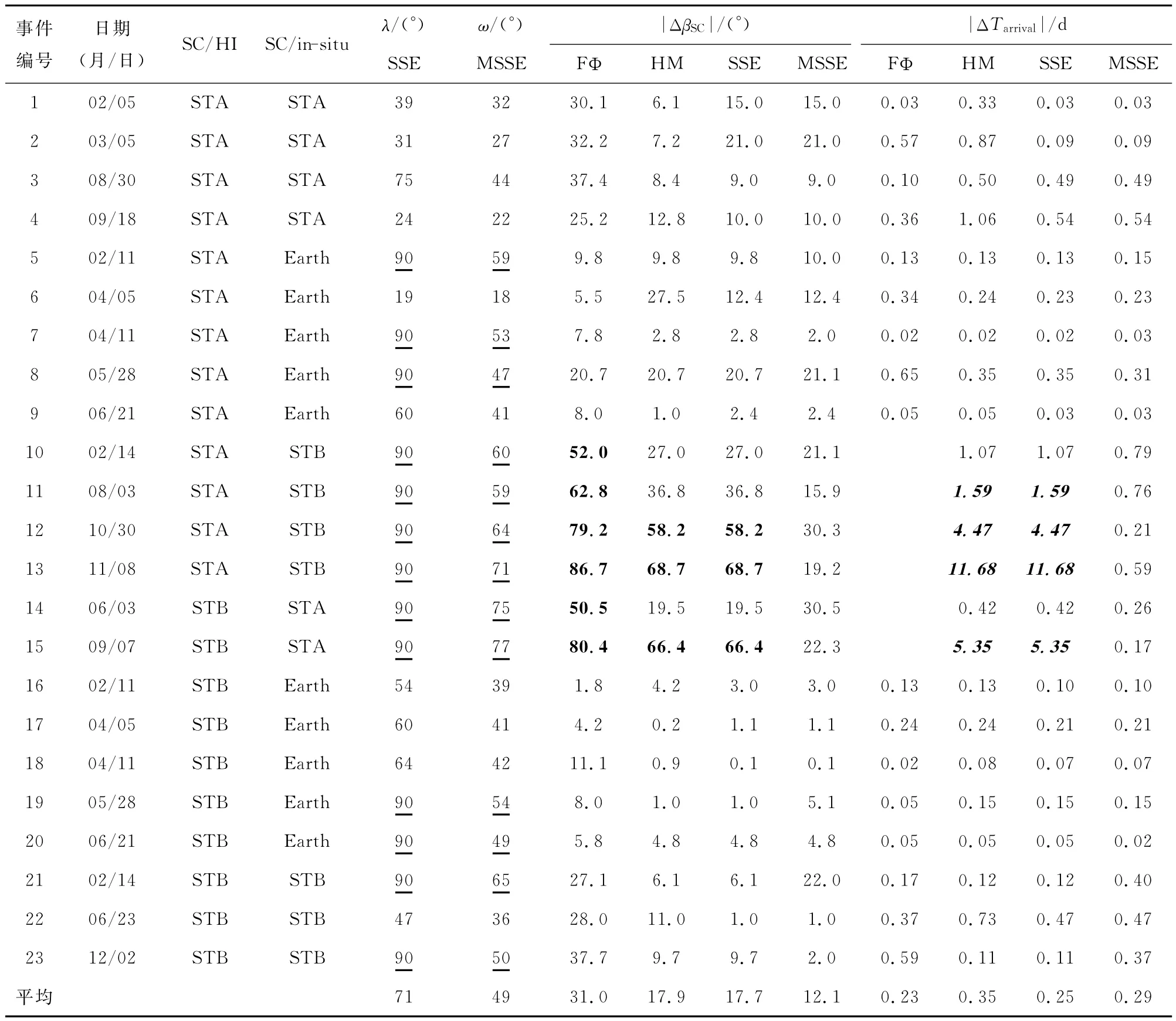
表1 CME事件列表Table 1 List of CME events

将提取的CME参数作为CME是否到达某颗卫星的预报参考时，使用FΦ、HM、SSE和MSSE拟合法的预报结果与ICME实测相符合的事件数分别是17、23、23和23个.

与HM拟合法相比，13个CME事件使用MSSE拟合法得到的主传播方向与实测ICME的卫星夹角｜ΔβSC｜减小，4个事件分析的预计到达时间误差增大，5个CME事件变化不超过0.01天，18个CME事件减小.与SSE拟合法相比，13个CME事件使用MSSE拟合法得到的主传播方向与实测ICME的卫星夹角减小，5个事件分析的预计到达时间误差增大，7个CME事件减小.在表1中用黑体标出｜ΔβSC｜超过40°的CME事件，与其他三种方法不同的是，使用MSSE拟合法提取的都不超过40°.

所有CME事件使用HM、SSE和MSSE拟合法得到的主传播方向与实测卫星之间的夹角的平均值分别是17.9°、17.7°和12.1°.13个CME事件（在表1中由下划线标出）使用MSSE拟合法提取的半圆锥角超过45°，也就是说，这些事件使用SSE拟合法提取的CME参数与使用HM拟合法提取的CME参数相同.所有CME事件使用MSSE拟合法提取的平均半圆锥角为49°，最大值和最小值分别为77°和18°.

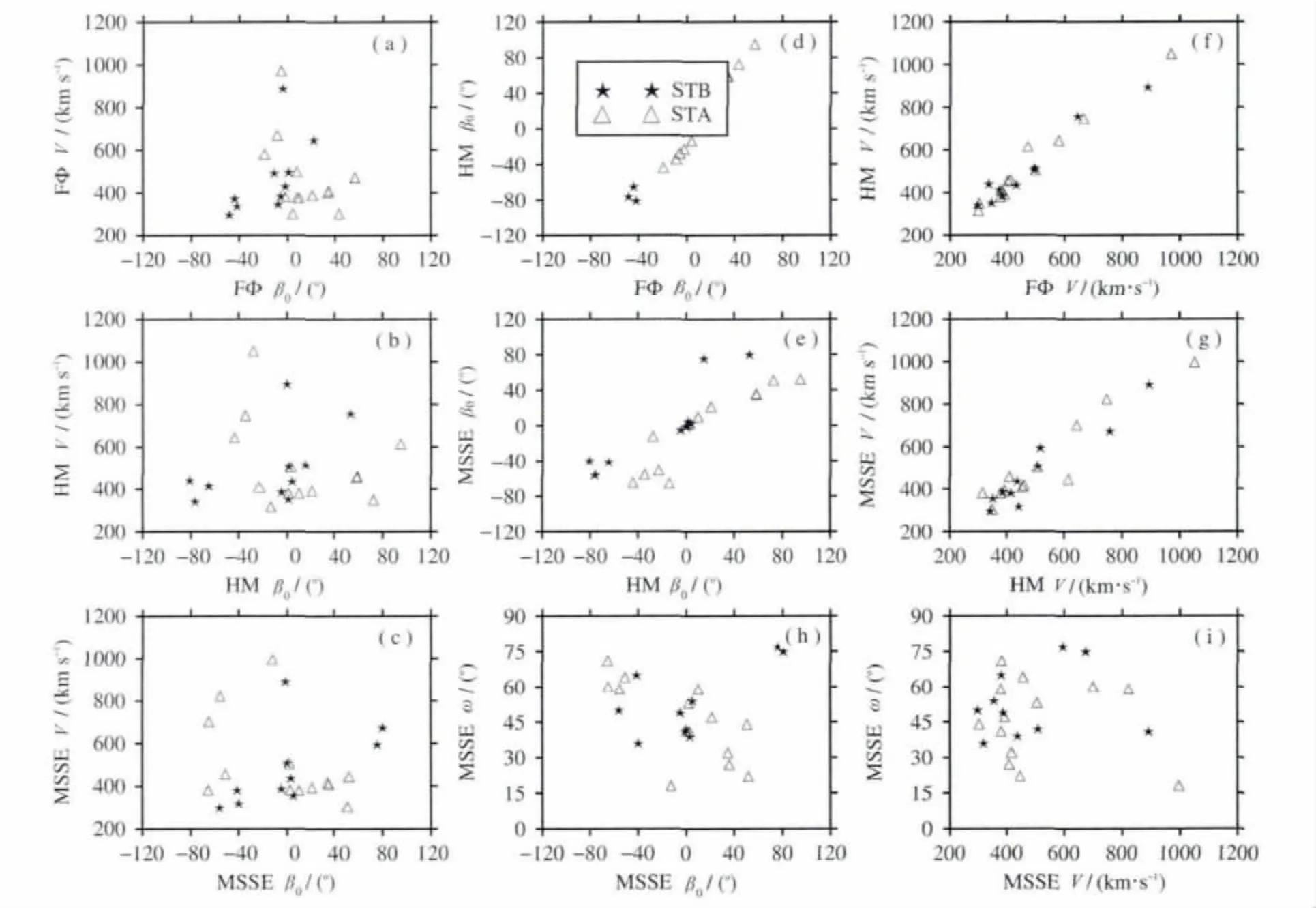
图6 三种方法提取CME参数的统计分析β0、V和ω分别表示三种方法提取的CME主传播方向、传播速度和半圆锥角，三角和星形分别表示STA／HI和STB／HI观测的CME事件.Fig.6 Statistical analysis of CME parameters derived by 3different methodsIn this figure，β0，Vandωrepresent CME direction of propagation，transit speed，and half-cone angle extracted by three methods，respectively.The triangles and stars represent CME events observed by STA／HI and STB／HI，respectively.

23个CME事件使用MSSE拟合法、19个CME事件使用HM和SSE拟合法得到的预计到达时间的平均误差分别是0.29、0.35和0.25天.

图7是根据这四种方法提取的CME参数分析的预报结果与实测ICME参数的误差直方图，第一幅图中1刻度表示能否到达某颗卫星的预报结果与这颗卫星的实测ICME结果相符合，0刻度表示预报结果与实测结果不符合；第二、三幅图分析的是预报结果与实测结果符合的事件；第二幅图是CME扫过这颗卫星的速度与实测ICME速度最大值的相对误差直方图；第三幅图是CME预计到达这颗卫星的时间与实测ICME起始时间的绝对误差直方图.

观察图7，我们发现：将提取的CME参数作为CME是否到达某颗卫星的预报参考时，使用HM、SSE和MSSE拟合法的预报结果比使用FΦ拟合法的预报结果好；预报CME扫过这颗卫星的速度和预计到达时间时，使用MSSE拟合法的预报结果最好，其次分别是SSE和HM拟合法.

3.2 进一步分析

在2.2.2节中已经介绍了本文中使用提取的CME参数分析CME事件是否能够到达某颗卫星时，是将对CME前沿的角宽度假设作为判断的重要参考，而使用MSSE拟合法时，是将对CME前沿的拟合圆锥角作为判断的重要参考.由MSSE拟合法拟合得到的圆锥角，相比FΦ、HM拟合法假设为定值的角宽度，更能体现CME参数与HI对CME前沿观测的依赖性.这三种方法假设CME前沿具有不同的形态，也使得本文利用这三种方法分析的CME预报结果差异很大.当CME的角宽度和拟合圆锥角较大时，很可能会先后或同时扫过多颗卫星.

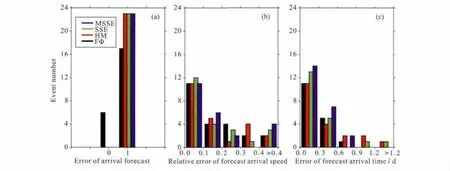
图7 预报误差直方图图中所示的是根据提取的CME参数分析的预报结果与实测ICME参数的误差直方图，第一幅图中1刻度表示能否到达某颗卫星的预报结果与这颗卫星的ICME实测结果相符合，0刻度表示预报结果与实测结果不符合；第二、三幅图分析的是预报结果与实测结果符合的事件；第二幅图是CME扫过这颗卫星的速度与实测ICME速度最大值的相对误差直方图；第三幅图是CME预计到达这颗卫星的时间与实测ICME起始时间的绝对误差直方图.Fig.7 Histogram of prediction errorIn this figure，histograms of error of prediction results extracted from fitted parameters of the CMEs，and in-situ observations of ICME.Left：whether the arrival forecast result is consist with in-situ observations or not（1as yes，0as no）.Middle：relative error of arrival speed of the CMEs and the maximum speed of the ICMEs.Right：error of arrival time of the CMEs with ICME start time.

图8 SECCHI／COR2（下）和LASCO／C2（上）观测到的三个CME事件从左至右分别是于10／30（左一）和11／08（左二）到达了STB卫星的2个CME事件，以及于09／07（右一）到达了STA卫星的1个CME事件.Fig.8 Observations of 3CMEs by SECCHI／COR2（down）and LASCO／C2（up）In this figure，the left images belong to CME arrived STB on Oct.30.The middle images belong to CME arrived STB on Nov.8.The right images belong to CME arrived STA on Sep.7.

利用HM拟合法提取的CME参数预报是否能够到达某颗卫星时，只有表1中编号4的事件预报结果是只可能到达STA卫星，编号1—3、8、14的5个事件预报结果是可能到达STA和ACE卫星，编号6、10—13、21—23的8个事件预报结果是可能到达ACE和STB卫星，编号5、7、9、15—20的9个事件预报结果是可能到达STA、ACE和STB卫星，但本文研究的23个事件中，都只在一颗卫星实地观测到对应的ICME事件.在10个ACE卫星被观测到ICME事件中，有8个事件使用HM拟合法分析的预报结果是可能先后或同时到达三颗卫星，这种预报结果的误差说明使用HM模型假设的角宽度180°作为预报的参考并没有收到很好的效果.

利用SSE拟合法提取的CME参数预报是否能够到达某颗卫星时，表1中编号1—2、4的3个事件预报结果是只可能到达STA卫星，编号6、9、16—18的5个事件预报结果是只可能到达ACE卫星，编号22的1个事件预报结果是只可能到达STB卫星，编号3、8、14的3个事件预报结果是可能到达STA和ACE卫星，编号10—13、21、23的6个事件预报结果是可能到达ACE和STB卫星，编号5、7、15、19—20的5个事件预报结果是可能到达STA、ACE和STB卫星.这说明SSE拟合法用于预报CME是否能够到达某颗卫星时，比HM拟合法更准确.

利用MSSE拟合法提取的CME参数预报是否能够到达某颗卫星时，表1中编号1—4、14—15的6个事件预报结果是只可能到达STA卫星，编号6—9、16—20的9个事件预报结果是只可能到达ACE卫星，编号13、21—23的4个事件预报结果是只可能到达STB卫星，编号5的事件预报结果是可能到达STA和ACE卫星，编号10—12的3个事件预报结果是可能到达ACE和STB卫星.利用MSSE拟合法提取的圆锥角作为预报参考时，只有8个事件的预报结果出现了可能先后或同时到达多颗卫星的情况，远少于利用HM和SSE拟合法假设的角宽度作为预报参考时出现同样情况的22和14个.因此，MSSE拟合法利用拟合圆锥角作为预报CME是否能够到达某颗卫星的参考，比HM和SSE拟合法更准确.这是由于在2.2.2节中提到的一个MSSE拟合法的特点：相比SSE拟合法对CME是否能扫过这颗卫星的预报结果，MSSE拟合法会造成预报结果被低估.

当利用多种方法的预报结果都是可能到达某颗卫星时，本文用预计到达时间的误差进一步比较这些方法用于预报的优劣.本文以编号12、13、15的3个事件为例，它们分别是由STA／HI观测到、分别于10／30和11／08到达了STB卫星的CME事件，以及由STB／HI观测到、于09／07到达了STA卫星的CME事件，图8是它们分别被SECCHI／COR2观测（图8下，来自http：∥stereo.gsfc.nasa.gov／cgi－bin／images［2012－06－06］）和LASCO／C2观测（图8上，来自http：∥sohodata.nascom.nasa.gov／cgi－bin／data＿query［2012－06－06］）.

这三个事件使用HM、SSE和MSSE拟合法分析的预计到达卫星都与实测ICME事件的卫星符合，但使用HM和SSE拟合法提取的CME参数分析的预计到达时间误差太大，甚至超过4天，很明显是不合理的，而使用MSSE拟合法提取的CME参数分析的预计到达时间误差却不超过0.6天，拟合半圆锥角分别是64°、71°和77°.这是由于 HM拟合法假设CME前沿是球形，当实测ICME事件的卫星与CME拟合主传播方向的夹角为θ时，卫星所在方向上CME前沿的传播速度就等于拟合主传播方向上CME前沿的传播速度与cosθ的乘积，而这三个事件使用SSE拟合法提取的CME参数与HM拟合法相同，所以，当θ不超过90°却很大时，卫星所在方向上CME前沿的传播速度就与拟合主传播方向上CME前沿的传播速度差异很大（前者是后者的0～1倍），从而造成预计到达时间误差的巨大差异.

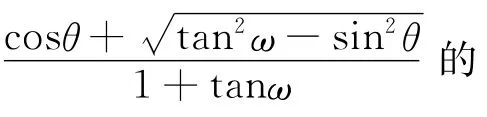
因此，利用MSSE拟合法提取的CME参数作为预报CME半球形前沿何时到达某颗卫星的参考，得到的预计到达时间误差的范围较小，明显小于HM和SSE拟合法得到的预计到达时间误差的范围.

综上所述，MSSE拟合法相比FΦ、HM和SSE拟合法，在用于预报CME事件是否能到达某颗卫星、何时到达时，不但可以更准确地拟合CME主传播方向和传播速度，也可以缩小预计到达时间和到达速度的误差.

4 结 论

自相似扩展拟合法（SSE）假设CME具有恒定角宽度、沿径向向外传播的自相似扩展的球形前沿，由日心出发的、与这个球形前沿相切的圆锥的圆锥角就是通常所说的CME角宽度，半角宽度取值范围是［0°，90°］，固定 Φ 角拟合法（Fixed－Φ，FΦ）和调和均值拟合法（Harmonic－mean，HM）分别对应SSE模型的半角宽度为0°和90°的特殊情况.

本文中修改后的自相似扩展拟合法（MSSE）假设CME具有自相似扩展的半球形前沿，能够提取的CME参数包括由日心出发的、圆锥截面过球心的圆锥的半圆锥角和CME的主传播方向、传播速度，半圆锥角取值范围是［0°，90°］，FΦ和 HM 分别对应MSSE模型的半圆锥角为0°和45°的特殊情况.MSSE拟合法扩大了SSE模型对CME前沿形态的描述范围，MSSE模型的半圆锥角为90°时，CME前沿是以日心为圆心的半圆.本文将MSSE模型的三个参数作为判断CME是否能够到达、何时到达某颗卫星的重要参数.

本文利用2010年STEREO卫星HI图像提取的、23个CME在太阳赤道平面上的运动轨迹，通过与STEREO和ACE卫星实测ICME参数的对比和统计，讨论了用于提取CME参数的FΦ、HM、SSE和MSSE拟合法的优劣.结果发现：在用于预报CME事件是否能到达某颗卫星、何时到达时，MSSE拟合法相比FΦ、HM和SSE拟合法，不但可以更准确地拟合CME主传播方向和传播速度，也可以缩小预计到达时间和到达速度的误差.

（References）

［1］Bewsher D，Harrison R A，Brown D S.The relationship between EUV dimming and coronal mass ejections.Astron.Astrophys.，2008，478（3）：897－906.

［2］Lippiello E，de Arcangelis L，Godano C.Different triggering mechanisms for solar flares and coronal mass ejections.Astron.Astrophys.，2008，488（2）：L29－L32.

［3］Wang Y M，Zhou G P，Ye P Z，et al.Orientation and geoeffectiveness of magnetic clouds as consequences of filament eruptions.∥Dere K P，Wang J，Yan Y，eds.Coronal and Stellar Mass Ejections，Proceedings of IAU symposium No.226.Beijing，China，2005：448－453.

［4］Burlaga L F E.Magnetic clouds.∥ Schwenn R，Marsch E eds.Physics of the Inner HeliosphereⅡ.Particles，Waves and Turbulence.Berlin：Springer，1991.

［5］Domingo V，Fleck B，Poland A I.The SOHO mission：an overview.Solar Physics，1995，162（1－2）：1－37.

［6］Brueckner G E，Howard R A，Koomen M J，et al.The large angle spectroscopic coronagraph （LASCO）.Solar Physics，1995，162（1－2）：357－402.

［7］Schwenn R，dal Lago A，Huttunen E，et al.The association of coronal mass ejections with their effects near the Earth.Ann.Geophys，2005，23（3）：1033－1059.

［8］Gosling J T.Coronal mass ejections and magnetic flux ropes in interplanetary space.∥ AGU Geophys.Monogr.Ser.Washington D.C.：American Geophysical Union，1990：18937－18949.

［9］Xie H，Ofman L，Lawrence G.Cone model for halo CMEs：application to space weather forecasting.J.Geophys.Res.，2004，109（A3），doi：10.1029／2003JA010226.

［10］Michalek G.An asymmetric cone model for halo coronal mass ejections.Solar Physics，2006，237（1）：101－118.

［11］Xue X H，Wang C B，Dou X K.An ice－cream cone model for coronal mass ejections.J.Geophys.Res.，2005，110（A8）：A08103，doi：10.1029／2004JA010698.

［12］St Cyr O C，Howard R A，Sheeley N R Jr，et al.Properties of coronal mass ejections：SOHO LASCO observations from January 1996to June 1998.J.Geophys.Res.，2000，105（A8）：18169－18185.

［13］Yeh C T，Ding M D，Chen P F.Kinetic properties of CMEs corrected for the projection effect.Solar Physics，2005，229（2）：313－322.

［14］Thernisien A F R，Howard R A，Vourlidas A.Modeling of flux rope coronal mass ejections.Astrophysical Journal，2006，652（1）：763.

［15］Kaiser M L，Kucera T A，Davila J M，et al.The STEREO mission：an introduction.Space Sci.Res.，2008，136（1－4）：5－16.

［16］Eyles C J，Harrison R A，Davis C J，et al.The heliospheric imagers onboard the STEREO mission.Solar Physics，2009，254（2）：387－445.

［17］Lugaz N，Hernandez－Charpak J N，Roussev I I，et al.Determining the Azimuthal Properties of Coronal Mass Ejections from Multi－Spacecraft Remote－Sensing Observations with STEREO SECCHI.The Astrophys.J.，2010，715：493－499.

［18］Sheeley N R Jr，Walters J H，Wang Y M，et al.Continuous tracking of coronal outflows：two kinds of coronal mass ejections.J.Geophys.Res.，1999，104（A11）：24739－24767.

［19］Davies J A，Harrison R A，Rouillard A P，et al.A synoptic view of solar transient evolution in the inner heliosphere using the Heliospheric Imagers on STEREO.Geophys.Res.Lett.，2009，36（2）：L02102，doi：10.1029／2008GL036182.

［20］Kahler S W，Webb D F.V arc interplanetary coronal mass ejections observed with the solar mass ejection imager.J.Geophys.Res.，2007，112（A9），doi：10.1029／2007JA012358.

［21］Lugaz N，Vourlidas A，Roussev I I.Deriving the radial distances of wide coronal mass ejections from elongation measurements in the heliosphere－application to CME－CME interaction.Ann.Geophys.，2009，27（9）：3479－3488.

［22］Davies J A，Harrison R A，Perry C H，et al.A self－similar expansion model for use in solar wind transient propagation studies.Astrophys.J.，2012，750（1）：23.

［23］Möstl C，Davies J A.Speeds and arrival times of solar transients approximated by self－similar expanding circular fronts.Solar Physics，2013，285（1－2）：411－423.