适用于MMC多端高压直流系统的精确电压裕度控制
胡静,赵成勇,翟晓萌
(新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
0 引言
基于电压源换流器的柔性直流输电(voltage source converter based high voltage direct current,VSCHVDC)系统,由于其有功与无功独立可控、可向无源网供电等优点,在风力发电并网、孤岛供电、大城市供电网络等领域得到了广泛应用[1-2]。随着经济发展和电网的大规模建设,必然要求电网能够实现多电源供电以及多落点受电[3-5]。同时,VSC-HVDC在潮流反转时电压极性不变的特点非常有利于构成并联型多端柔性直流输电系统(VSC based multi-terminal DC transmission system,VSC-MTDC)。基于VSC-MTDC系统能充分发挥VSC的技术优势,是MTDC系统的发展趋势。
目前,VSC-HVDC的换流器拓扑主要有两电平、三电平和模块化多电平换流器(modular multilevel converter,MMC)结构。由德国学者于2002年提出的MMC结构,采用子模块串联构成换流阀,与两电平VSC相比,具有输出电压更接近理想正弦波形、开关频率低、损耗小、故障穿越能力强等特点[6-9],已成为优选的拓扑。基于MMC的多端直流输电(MMC based multi-terminal DC transmission system,MMC-MTDC)技术,比两电平VSC多端系统输出特性更优,应对直流侧故障的故障穿越能力更强,兼具经济性和可靠性优势,具有广泛的应用前景[10]。
多端直流技术的核心也是难点就是多端协调控制保护策略。早期的研究采用的是单点直流电压控制法(也称为主从控制[11-12]),多端系统中只有一端负责控制直流电压,其余端各自控制电流或功率。这种控制策略的缺陷是当控制直流电压的端遭受交直流侧故障时,或退出运行,或改为定直流电流(定功率)控制,整个多端系统失去调节直流电压的能力。因此,对于并联型多端系统,必须要实现多点直流电压控制,即系统中要有大于等于2个端具备控制直流电压的能力。目前,针对于并联型VSC-MTDC系统的多点直流电压控制主要有带电压下降特性的控制法[13-15](也称为分散协调控制)和电压裕度控制法[16-19](也称为改进主从控制法)2类。前者控制灵活简单,但在功率发生大扰动时,直流电压偏离较大;后者将主站与从站的电压定值拉开一定裕度,控制特性良好,受到大功率扰动时仍可实现控制方式自主快速切换。
多端直流系统中的直流电压与交流系统中的频率概念相似,定电压控制实质上是对直流系统的有功功率进行平衡。然而,与交流系统有统一的频率不同,由于直流线路电阻的存在,导致不同端的直流电压存在微小差别。随着输电距离的不断增长,线路电压降落和线路损耗对电压裕度控制的影响不可忽略不见。本文在分析线路电压降与线路损耗对电压裕度控制带来的影响的基础上,提出精确电压裕度控制方法,得出电压裕度计算公式,并设计出精确电压裕度控制器。
1 MMC-MTDC系统模型
1.1 MMC系统结构
MMC由6个桥臂组成,其中每个桥臂由若干个相互连接且结构相同的子模块(sub-module,SM)与1个电抗器串联组成[20-21]。图1所示为MMC的主电路和每个SM的拓扑结构图。如图1(b)所示,MMC的每个子模块都可是视作1个二端口网络,由1个作为开关单元的绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)半桥(包括T1和T22个IGBT以及D1和D22个反并联二极管)和1个直流储能电容构成。

图1 MMC拓扑结构Fig.1 Topological structure of MMC
当全控型器件T1导通,T2关断时,子模块输出电压为直流电容电压u0;当T1关断,T2导通时,子模块输出电压为0。桥臂电压为桥臂上所有串联的子模块输出电压之和,而直流电压udc为同一相上、下桥臂电压之和。
由于MMC的桥臂电压是由桥臂上子模块开通子模块个数决定,因此可以将MMC的桥臂电压等效为可控电压源,则单端MMC-HVDC的等效主电路拓扑如图2所示。
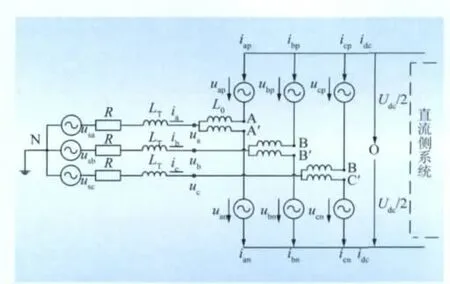
图2 MMC-HVDC等效电路图Fig.2 Equivalent circuit diagram of MMC-HVDC
图2省略了换流变压器。图中:usi(i=a,b,c)为三相交流系统的电压值;R为表示线路和变压器损耗的等效电阻;LT为换流变压器的漏抗;ui为MMC三相的出口电压值;ii为交流系统的三相交流电流值;uip和iip为MMC三相上桥臂电压和电流;uin和iin为MMC三相下桥臂电压和电流;idc为直流电流;Udc为直流电压;N点为交流系统中性点,O点为直流侧的等效零电位点,两者必有一点接地;A点与A'点为等电位点,三相等位点电压为uei。
1.2 MMC-MTDC的dq坐标模型
为了得到多端柔性直流输电系统的数学模型,本文选择基于MMC的三端柔性直流输电系统(如图3所示)为例进行数学模型推导。该系统由3个基于MMC拓扑结构的电压源型换流器构成,其直流侧通过直流网络并联连接。3个换流器分别与各自独立的交流系统相连,均具有功率的双向传输能力。
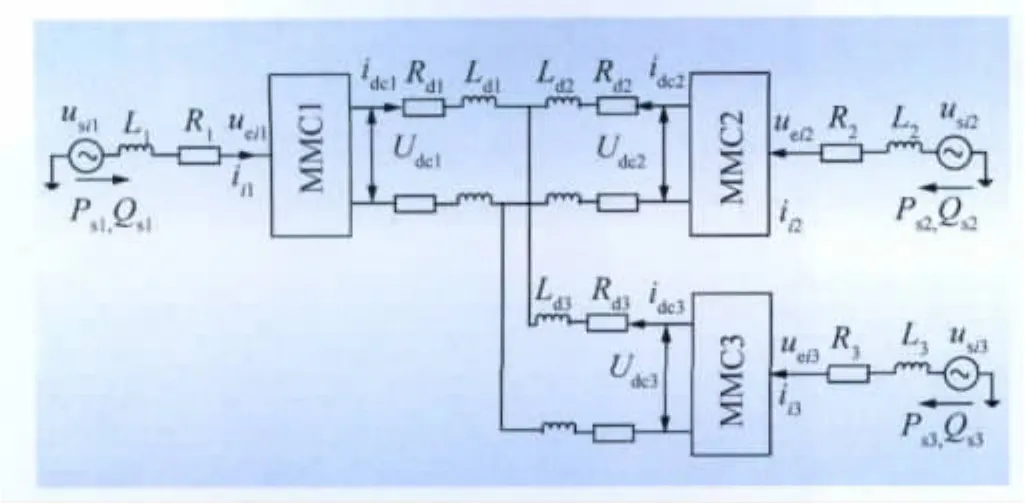
图3 三端MMC系统结构示意图Fig.3 Structure of 3-terminal MMC system
图3中:Lm(m=1,2,3,表示端数)为变压器漏抗和桥臂电抗串联后的等效电抗,其表达式为

根据基尔霍夫电路定律,可得三端柔性直流输电系统换流站交流侧方程组为

其中:Km表示直流电压利用系数;δm表示换流站输出电压与系统电压的夹角。
将式(2)转换到dq坐标,得到
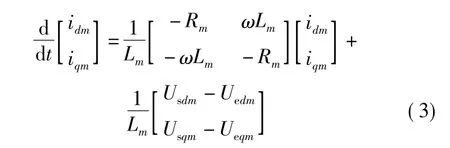
三端MMC-HVDC系统直流侧电压、电流的表达式为

式中:Vm为三端直流系统直流线路并联连接点的等电位电压值。由于直流电流波动较小,可认为≈0。
换流器交流侧注入换流器的有功功率和无功功率分别为
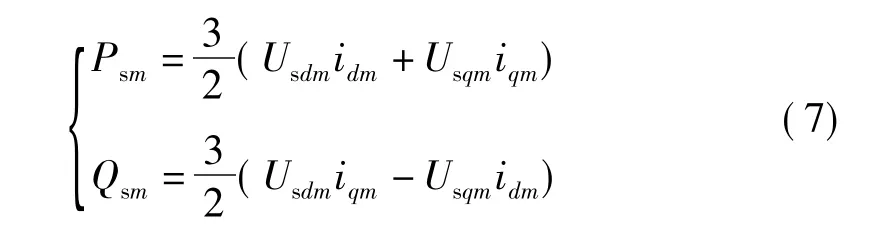
在三相电网电压平衡条件下,取电网电压矢量方向为d轴方向,有Usdm=Us,Usqm=0,则上式可简化为
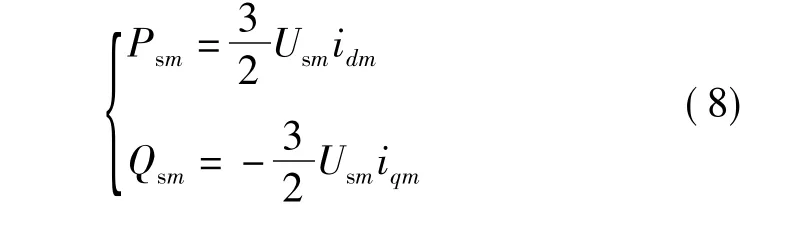
三端柔性直流输电系统直流侧功率为

忽略R和换流器损耗,则注入换流站的有功功率应该等于换流站输出到直流输电线路的功率,则有
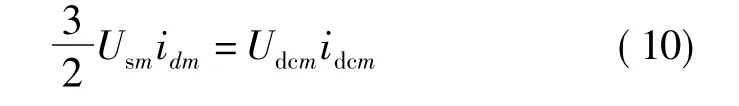
式(3)—(6)和(10)即为三端柔性直流输电在dq坐标系下的数学模型。当柔性直流系统多于三端时,可以推导出类似的数学模型。从上述数学模型可知,多端系统中的各端均可采用矢量控制,但要协调好各端外环的电压定值和功率定值,保证直流侧的功率平衡。
2 精确电压裕度控制
2.1 电压裕度控制
直流电压恒定是多端柔性直流输电系统稳定运行的前提,用于多端系统的电压裕度控制法通过各端直流电压定值的配合,对直流电压调节和功率控制性能都具有良好的刚性。电压裕度控制又分为单裕度和双裕度控制,双裕度控制应用范围更宽泛,适用于工况复杂多变的多端系统。
采用双电压裕度控制方式的系统电压-功率运行特性如图4所示。图中虚线矩形框表示各端的交流有功功率输出上、下限(Pmax和Pmin)与直流电压的安全运行上、下限(Udmax和Udmin)。各换流站的运行点都应位于虚线框内部。换流站Ⅰ为主站,一般与较强的交流系统相连,功率调节范围很宽。换流站Ⅱ为从换流站,采用电压裕度控制,与主换流站的电压参考值相差2个电压裕度,分别为正电压裕度和负电压裕度。电压裕度值由上层控制器确定,具体数值的选择并没有准确的依据,一般按照经验可选择5% ~10%。换流站Ⅲ为定功率控制,功率输出稳定在功率参考值。如果换流站Ⅲ接无源系统,仅采用定交流电压控制,其控制特性同定功率类似,不过功率参考值的竖线会随负荷变动而左右平移。

图4 双电压裕度法控制特性Fig.4 Control characteristics of double voltage margin method
如图4所示,三端系统在正常工作状态下,换流站Ⅰ采用定直流电压控制,换流站Ⅱ、III采用定有功功率控制,系统稳定运行于工作点A,此时换流站Ⅰ向换流站Ⅱ、Ⅲ供电(以换流站向直流网络输送功率为正方向)。当换流站Ⅲ的有功功率需求增加后(如虚线所示),换流站Ⅰ通过增大输出功率来维持系统功率平衡,当换流站Ⅰ输出功率达到极限时,系统的运行点到达B,换流站Ⅰ将无法调节直流电压。若运行点B的功率仍然无法平衡则系统将不能稳定,直流电压下降,此时需要其他换流站代替换流站Ⅰ来承担调节直流电压的任务并分担功率,因此换流站Ⅱ由原来的定功率控制转换为定直流电压控制,系统的运行点从B移至C,换流站Ⅰ由原来的定直流电压控制方式转换为定有功功率控制模式。当换流站Ⅰ由于故障等原因退运时,换流站Ⅱ可以由定功率控制转化为定电压控制,系统运行点从A移到D点。
同样,如果换流站Ⅲ的有功功率需求突然减少,甚至功率反送,或换流站Ⅰ在退运前处于逆变方式,则有可能使得换流站Ⅱ的运行点向上移动到达电压正裕度UdrefH。
2.2 精确电压裕度控制
上述电压裕度控制忽略了直流电流电阻,认为多端系统中各端的直流电压相等,都等于定直流电压端电压定值。然而,当直流线路到达一定长度时,线路电阻Rd不可忽略。由式(4)、(5)可知,Rd引起的线路电压降落RdIdc,使各端的直流电压产生较大偏差。图5为考虑直流电压降落和线路功率损耗后的电压裕度控制特性。

图5 精确电压裕度控制特性Fig.5 Control characteristics of precise voltage margin method
如图5所示,不考虑线路阻抗影响的理想电压裕度控制下的系统运行点为A点。设3端的直流母线电压值分别为Udc1、Udc2和Udc3,交流侧有功功率(除去换流器损耗)分别为P1、P2和P3,参照图3所示系统结构图,可以得出
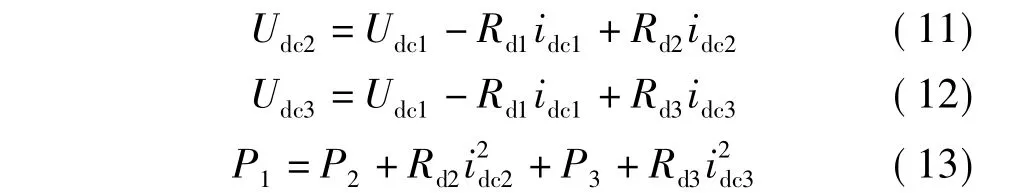
式中:Udc1=Ud1ref=C1,P2=P2ref=C2,P3=P3ref=C3,C1、C2、C3为常数。
因此,系统的实际运行点如图5中B点所示,换流站Ⅱ、Ⅲ的直流电压均低于换流站Ⅰ的直流电压参考值,而换流站Ⅰ的发送功率实际高于其余2站吸收功率之和。当换流站Ⅱ的电压参考值低于换流站Ⅱ实际运行点电压时,系统能够维持稳定,直流电压由换流站Ⅰ控制。但如果换流站Ⅱ的电压裕度取值较小,使其电压参考值高于实际运行电压,则换流站Ⅰ和换流站Ⅱ都处于定直流电压方式,换流站Ⅱ失去功率控制能力,系统运行于图中C点,此时系统稳定性较差。
3 电压裕度值选取
电压裕度值的选取很关键,裕度差选小会导致同时多个点定直流电压,系统功率紊乱,选取过大又会使扰动后的系统直流电压过低或过高,且直流电流波动过大。考虑到线路电压降对电压裕度的影响以及直流电压的运行范围,可得到电压裕度值ΔU的选取公式为

式中:rj为直流架空线或电缆的单位长度电阻;lj为线路长度;j表示欲求电压裕度的两端之间的不同型号的导线段;Udcref为主换流站的直流电压参考值;Udrop表示从站与主站之间的直流线路电压降落,与线路长度及直流电流(或该端有功功率)密切相关;Δ为控制偏差,正比于主站电压参考值,取值为定值,一般数值较小,包括忽略线路电容产生的电压降部分以及为避免运行点频繁转换的裕度电压参考值与实际运行点之间的分隔差值;k为百分比系数,可取1% ~5%,直流线路为电缆时k的取值比架空线稍大。
因此,从站的裕度电压值的上、下限为
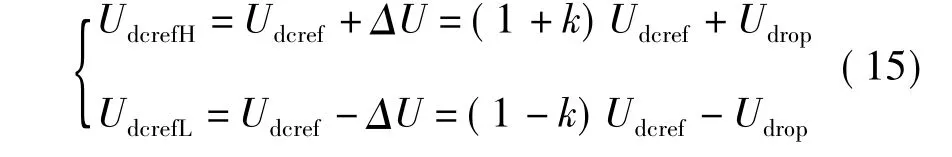
根据电压裕度的公式,可以对电压裕度控制器进行改进,优化系统控制性能。基于精确电压裕度控制的控制器结构如图6所示。

图6 精确电压裕度控制器结构Fig.6 Structure of precise voltage margin controller
Udrop的初始值可以由BPA等机电暂态程序软件通过潮流程序快速算出,之后,Udrop可根据系统中的直流电流测量值的变化适当调整,从而对电压裕度进行优化。
4 仿真分析
为了对本文提出的精确电压裕度控制理论以及所设计的精确电压裕度控制器进行验证,在PSCAD/EMTDC仿真环境下搭建了三端21电平MMC-HVDC模型,系统结构如图3所示。3个换流站采用3段100 km长的双极电缆模型并联连接,电缆单位电阻为0.08 Ω/km。各站的主要参数和初始控制参考值如表1所示。

表1 仿真模型系统参数Tab.1 System parameters of simulation model
4.1 验证裕度取值对系统控制特性的影响
三端MMC系统按照表1中的参考值后,可由潮流程序计算出各端运行点功率电压值如表2所示。

表2 初始值潮流计算结果Tab.2 Initial value results from load flow calculation
由表2可看出:换流站Ⅱ、III的直流电压都与换流站Ⅰ设定的参考值有很大偏差,而换流站Ⅰ所输送的功率值也高出逆变站吸收功率之和。
若按照以往的经验值将电压裕度值选为主站直流电压参考值的5%,则换流站Ⅱ的电压参考值下限设置为380 kV,在2.5 s时,将换流站Ⅱ的UdcrefL从370 kV改为380 kV,其余控制量不变,仿真结果如图7所示。
由图7可看出:当电压裕度设置不合理时,换流站Ⅱ在系统没有受到扰动的情况下,改变了控制方式,并和主站同时控制直流电压,系统运行稳定性降低。因此,对电压裕度的精确控制是十分必要的。
4.2 验证精确电压裕度控制法的效果
换流站Ⅱ采用图6所示的精确电压裕度控制器,k取4%,换流站Ⅱ的UdcrefL初始值为370 kV,1.5 s后导入式(15)进行实时计算。在2.5 s后,将换流站Ⅲ功率定值由-150MW改为-300MW。其他控制参量均按照表1进行设定。仿真结果如图8所示


图8(a)、(b)分别为各端的有功功率和直流电压变化曲线,图8(c)为换流站Ⅱ电压定值下限变化波形。如图所示,1.5 s后,UdcrefL从370 kV上升为372.3 kV,且各端的直流电压和功率保持不变,说明电压裕度的优化调整并没有给系统稳定性带来影响。当2.5 s后换流站Ⅲ的功率定值发生阶跃,换流站Ⅰ达到功率输出极限,由定电压转换为定功率,换流站Ⅱ随之从定功率控制转变为定电压控制,定值为优化后的UdcrefL,整个转化过程快速平稳。换流站Ⅱ电压定值由于换流站Ⅲ直流电流的剧增发生瞬间的波动,但对整个系统的直流电压与功率没有造成影响。
5 结论
本文首先推导了MMC-MTDC系统的数学模型,然后从理论和仿真2个方面分析了长距离线路电压降落与线路损耗对电压裕度控制带来的影响,提出精确电压裕度控制的理论,并给出了精确电压裕度值选取公式,同时相应设计了精确电压裕度控制器。以多端MMC系统为模型进行了电磁暂态仿真,仿真验证表明,该方法能够实现对多端系统的精确控制,可以实时优化电压裕度值的选取。当系统遭遇功率扰动时,控制器能够进行控制模式的自主切换,平衡功率波动,维持MMC-MTDC系统稳定运行。
[1]汤广福.基于电压源换流器的高压直流输电技术[M].北京:中国电力出版社,2009:2-13.
[2]赵成勇,李金丰,李广凯.基于有功和无功独立调节的VSC-HVDC控制策略[J].电力系统自动化,2005,29(9):20-24.
[3]张文亮,汤涌,曾南超.多端高压直流输电技术及应用前景[J].电网技术,2010,34(09):1-6.
[4]Kundur P.Power system stability and control[M].New York:McGraw Hill,1994:538-544.
[5]赵畹君.高压直流输电工程技术[M].北京:中国电力出版社,2004:459-464.
[6]Lesnicar A,Marquardt R.An innovative modular multilevel converter topology suitable for a wide power range[C]//2003 IEEE Bologna Power Tech Conference,Bologna,Italy:IEEE/PES,2003:1-6.
[7]Lesnicar A,Marquardt R.A new modular voltage source inverter topology[C]//10th European Conference on Power Electronics and Applications,Toulouse,France:European Power Electronics and Drives,2003:1-5.
[8]Dorn J,Huang H,Retzmann D.A new multilevel voltage-sourced converter topology for HVDC applications[C]//CIGRE session 42,Paris,France:CIGRE,2008:19-21.
[9]Ding G J,Tang G F,He Z Y,et al.New technologies of voltage source converter(VSC)for HVDC transmission system based on VSC[C]//2008 IEEE Power and Energy Society General Meeting,Pittsburgh,USA:IEEE/PES,2008:1-8.
[10]Adam G P,Anaya-Lara O,Burt G.Multi-terminal DC transmission system based on modular multilevelconverter[C]//2009 Proceedings of the 44th International Universities Power Engineering Conference(UPEC),Glasgow,United Kingdom:IEEE,2009:1-5.
[11]Jiang H B,Ekstrom A.Muliterminal HVDC in urban area of large cities[J].IEEE Trans on Power Delivery,1998,13(4):1278-1284.
[12]Sakamoto K,Yaijima M.Development of a control system for a high performance self-commutated AC/DC converter[J].IEEE Trans on Power Delivery,1998,13(1):225-232.
[13]Xu L,Williams B W,Yao L Z.Muti-terminal DC transmission system for connecting large offshore wind farm[C]//2008 IEEE Power and Energy Society General Meeting,Pittsburgh,USA:IEEE,2008:1-7.
[14]Prieto-Araujo E,Bianchi F D,Junyent-Ferre A,et al.Methodology for droop control dynamic analysis of multi-terminal VSC-HVDC grids for offshore[J].IEEE Trans on Wind Farms Power Delivery,2011,26(4):2476-2485.
[15]陈谦,唐国庆,潘诗锋.采用多点直流电压控制方式的VSC多端直流输电系统[J].电力自动化设备,2004,24(5):10-14.
[16]Seki N.Filed testing of 53 MVA three-terminal DC link between power system using GTO converters[C]//IEEE Power Engineering Society Winter Meeting,Las Vegas,USA:IEEE,2000:2504-2508.
[17]Nakajima T,Irokawa S.A control system for HVDC transmission by voltage sourced converters[C]//IEEE Power Engineering Society Summer Meeting,Edmonton,Canada:IEEE,1999:1113-1119.
[18]陈海荣,徐政.适用于 VSC-MTDC系统的直流电压控制策略[J].电力系统自动化,2006,30(19):28-33.
[19]Haileselassie T M,Molinas M,Undeland T.Multi-terminal VSCHVDC system for integration of offshore wind farms and green electrification of platforms in the North Sea[C]//Nordic Workshop on Power and Industrial Electronics,Espoo,Finland,2008:1-8.
[20]屠卿瑞,徐政,郑翔.模块化多电平换流器型直流输电内部环流机理分析[J].高电压技术,2010,36(2):547-552.
[21]王姗姗,周孝信,汤广福.模块化多电平电压源换流器的数学模型[J].中国电机工程学报,2011,31(24):1-8.

