疏散规划的一种优化算法

尹大朏，方裕

（1.清华大学地球系统科学中心，北京 100871；2.北京大学遥感应用研究所，北京 100871）

0 引言

随着全球气候变化的加剧，大规模极端自然灾害的发生频率越来越高，地震、火山爆发、泥石流、海啸、台风、洪水等突发性自然灾害直接危害着居民安全；与此同时，人为造成的灾难事故如油气泄漏、火灾、恐怖袭击等对社会经济的影响也越来越大。这些灾害发生突然，影响范围极大，需要疏散的群众众多，如果缺乏有效的疏散策略和最佳的避险路径，极有可能在逃逸过程中造成不必要的拥堵，甚至造成二次伤害。为此有必要快速生成疏散规划（Evacuation Planning），尽快为处于危险地点的人群指派合理的路径，最大限度地利用路网的容量，同时尽可能减少拥堵，使居民尽早抵达安全地点。

疏散规划不仅需要为每个待疏散者找到快速抵达安全目的地的路径，还要保证这些路径不相互冲突。疏散规划方案的实质在于处理大量疏散人群和有限路网容量之间的矛盾，而疏散算法的难点在于如何尽快地得到合理的疏散规划方案。因为疏散算法需要从多个源点、多个时间点出发的路径组合中寻找最优，而且疏散算法允许逃生者在任意节点停留任意时间，这样问题寻优搜索的空间极大。

前人的探讨集中在疏散规划问题最优解的算法，其主要思路是将疏散规划问题转换为时变路网上的线性规划或者最小代价流问题求解［1，2］，最好的算法其时间复杂度为O（N6（T＋1）6）［3］。由于最优化解法需要在时间片上对路网进行复制，占用大量内存，导致算法很难扩展到大路网上，近年来许多研究者转向计算速度较快的次优解的研究。目前已知求解速度最快的次优解算法是由Shekhar研究组提出的启发式算法CCRP（Capacity Constrained Route Planning），其时间复杂度为O（P（E＋N）logN）［4－6］。然而，文献［7］使用小型城镇的路网对CCRP进行测试，发现计算时间超过1天，这显然无法达到应急指挥的要求。为此本文提出一种新型的启发式算法CCRP＋＋，进一步加速计算。其主要原理是引入一个双优先队列（Double Priority Queue），保存历史迭代计算的中间结果并启发当次迭代的搜索，以便删减CCRP中大量不必要的最短路径计算，达到大幅加速疏散规划计算的目的。虽然还有不少文献［8－20］对相关的问题进行了探讨，但至今还没有适用于大规模路网的高效算法。

1 问题定义与假设

在本文的算法探讨中，把问题抽象到一个时变的容量受限图G（N，E，S，D，P，T）中进行讨论。其中，N表示图节点（Node）的集合，E表示边（Edge）集合，S表示源点（Source）的集合，D 表示目标点（Destination）集合，P 表示疏散者（evacuees）的集合，T表示疏散过程经历的时间（Time）。每个源点表示危险地点，里面有数量不等的待疏散者，需要将其疏散到若干安全的目标点。路网由边及节点构成：边有通过时间（Travel Time）和边容限（Edge Capacity）两个属性，分别表示通过此边的时间和同时进入某一个边的最大人数；节点有节点容限（Node Capacity），表示同时刻不能有更多的人进入该节点。在疏散过程中，会有一定的人流（flow）通过特定的路径从某源点出发到达目标节点。

如图1的疏散网络示例中，3个源节点N1、N2、N8分别有10人、5人、15人，需要将这些人通过如下的网络尽快疏散到N13和N14。对应的疏散方案之一是表1展示的A－I共9组疏散流。以A组为例，在T0时刻从源点N8出发，经过（N8，N10）边于T3时刻到达N10，不做停留继续沿（N10，N13）边于T4到达安全目标点N13。疏散规划的目的是对网络中的路径进行合理配置（表1），分批次将人流疏导到不同目的地。

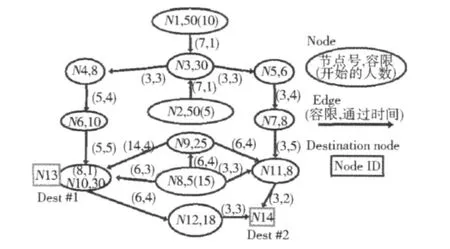
图1 疏散网络示例Fig.1 Evacuation network example

表1 疏散路径示例Table 1 Example of evacuation route

问题的定义如下：

给定：拥有如下性质的交通路网G（N，E，S，D，P，T），包含：1）1个源点（Sources）集合S，每个源点上有若干待疏散人；2）1个目标点（Destination）集合D；3）每条边的长度（Length）是其通过时间（Travel time）；4）边和节点都有其最大容限（Capacity）。

输出：1个“疏散流”集合，每个疏散流包括流量大小、通过的路网节点、从每个路网节点开始的出发时间（Depart Time）和抵达时间（Arrival Time）。

约束：主要的约束有：1）路网的容限限制，即同时进入一条边的人数不能超过路网的最大容限Capacity；2）先入先出准则FIFO，即进入同一条路段的人流，先进入该路段首节点的人抵达该路段末节点的时间必定不慢于后进入的人。

目标：优化的目标主要取决于：最小化总体逃逸时间（Egress Time）和最小化疏散规划生成所需的计算时间（Computational Time）。

值得注意的是，两个目标是对问题两个方面的优化目标。一般而言，无法同时达到最优，即在缩短的计算时间和求得问题的最优解之间存在一个制衡（Tradeoff）。在解决实际问题中，如果求得最优解的运行时间太长，可以选择计算速度较快的启发式算法求得问题的次优解（sub－optimal solution）。

2 疏散问题的CCRP算法

CCRP算法的核心思想是将疏散问题从网络流问题转换为迭代最短路径的计算问题。如图2所示，它添加一个虚拟的超级源点，每次计算当前系统中的一条“最早抵达路径”，即所有源点的最短路径的最小者，并将该路径上相应时刻的边容限预留给通过的人流。其主要计算思路可以概括为：如果在任一源节点上还有人，那么循环执行如下步骤：1）计算“最早抵达路径”（Earliest Arrival Path）；2）确定最早抵达路径上的流量（flow）；3）预约（Reserve）最短路径上面的边，转步骤1继续。

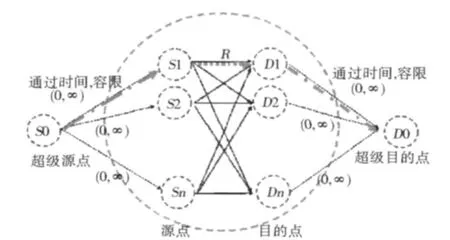
图2 CCRP将疏散问题转化为最短路径计算Fig.2 Converting the evacuation to shortest path calculation by CCRP

CCRP算法的时间复杂性：算法需要在每次迭代中为每个源节点计算一次最短路径，然后进行预留；寻找流量flow和reserve分别需要O（E）的时间，主要的时间消耗在最短路径搜索上。如果加入一个超级节点S0，可以把多源的最短路径转换为从S0出发的单源最短路径，则采用Dijkstra算法计算单源最短路径的时间复杂性为O（（E＋N）logN）；而在最坏情况下，每次迭代只能疏散一个人。所有源点的疏散者总和为P，因此CCRP算法的时间复杂性为O（P（E＋N）logN）。

其中，第一步使用Dijkstra算法对所有S个源点分别求解其到任意一个目标点的最短路径，取其中最短的一条作为“最早抵达路径”；在实现中，还可以加入一个超级源点（Super Source）来降低搜索的复杂性。第二步确定路径流量，需要比较最早抵达路径对应的源点中剩余疏散者人数和路径中各个路段的最小可用容限（Available Capacity），取较小者作为flow值；第三步预约（Reserve）路径，对找到的“最早抵达路径”的每个节点和每条路段的“边／节点可用容限表”的相应时刻减去flow值。

3 新型算法CCRP＋＋

3.1 CCRP算法的缺陷

CCRP算法的一个主要问题是为了获得当前的“最短的最短路径”需要在每次迭代中重复对所有源点求解其最短路径，计算的时间复杂性为O（P（E＋N）logN）。值得注意的是，CCRP采用了图2所示的一般图论模型进行分析，然而它忽略了路网的空间邻近性和迭代计算间的时间相关性。事实上，道路网络中的节点，无论是源点、目标点还是中间节点，都有其空间位置属性。CCRP采用适用于一般网的模型研究路网问题，而没有考虑路网的空间特性和疏散问题的时间特性。

如果对相邻两次迭代间源点的扩张过程进行“空间分析”，就可以更加直观地发现这些没有结束的“冗余扩张”较多（S－1个），以至于占据了单次迭代中大部分的运算时间（有用的扩张只有一个）；而且这些没有完成的扩张还会不断地重复，直到其中的某一个变成有用的扩张为止。在此把这些看似无用的最短路径计算称为“冗余重复”扩张。在图3所示的网络中有3个源点S1、S2、S3和3个目的节点D1、D2、D3。第一次迭代中，只有S1－D1（源－目标）节点对完成了扩张，第二次迭代中只有S2－D2完成了扩张。两次相邻迭代中，S3的扩张是冗余且重复的。

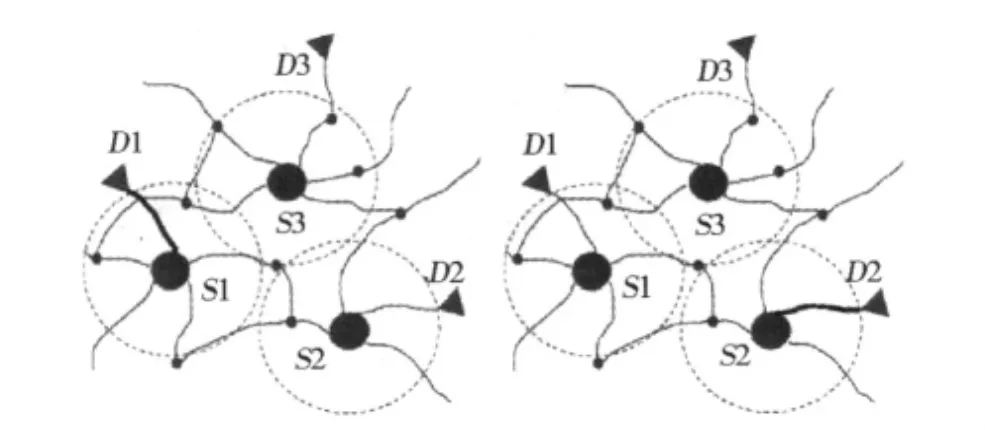
图3 两次相邻迭代 “冗余重复”扩张Fig.3 The redundant expansion in adjacent iterations

倘若能够消除这些冗余重复扩张，将大大提升算法效率，但是难点在于：虽然在所有的S个源点的最短路径搜索扩张中，有用的扩张只有一个，可是如果不对所有的源点进行最短路径计算，则无法知道哪一个是有用的扩张。虽然无法在每次迭代中不经过计算就确定当前迭代的有效扩张源点，但是通过观察多次迭代的扩张过程，可以获得一部分各源点距离其较近的目标节点的路径长度信息，利用这些历史迭代累计信息有望减少未来迭代中冗余扩张的次数。

3.2 CCRP＋＋ 算法

根据以上观察和分析，本文给出一种新的启发式算法CCRP＋＋。算法的核心思想与CCRP略有不同，使用历史上计算的最短路径长度启发搜索当前迭代中有可能是“最短的最短路径”的源点。为了保存历史上的最短路径信息，算法采用一种排序数据结构——优先队列（Priority Queue），保存每个源节点已经预留的路径长度，即从该源点到达最近目标点的最早抵达时间Earliest Arrival Time（缩写为EA）。每次迭代，只需提取优先队列最顶端的源点并进行最短路径计算，然后再放回队列中。

在实现中，首先对所有源点进行最短路径计算，以＜源点号，路径长度＞作为优先队列的＜Key，Value＞。为了保证每个源点在放入优先队列之前，不会因为其他节点的路径预订使得自身的最短路径失效，算法采用了双优先队列（Double Queue）设计，设置PreRQ（Pre－enter Reserved Queue）和 RQ（Reserved Queue）两个队列，将尚未进入正式预订队列RQ的源点，依照其“可用”路径的长度置于PreRQ中。每次迭代中，算法同时取出PreRQ和RQ的顶端源点，比较其路径长度。如果PreRQ顶端源点的路径长度较小，说明此时其为“最短的最短路径”，将其路径“预留”并置入RQ中；若RQ顶端源点的路径长度较小，则说明其为当前“最短的最短路径”，对其路径进行“Update”更新操作，将更新后的路径重新置入RQ中。这种通过取PreRQ和RQ的顶端元素进行比较的方法，可以迅速找到需要进行单源最短路径计算的源点，避免了每次迭代进行冗余重复的最短路径计算，大大提高了运算速度。算法的伪代码如下：

3.3 算法的复杂性分析

相对于CCRP，CCRP＋＋算法每次迭代只进行一次最短路径计算，但是多了两个从PreRQ和RQ取顶端源点和放回的操作，其复杂性分别为O（1）和O（logS），所以CCRP＋＋的复杂性为O（P（E＋N）logNlogS）。由于一般路网为稀疏图，E是N 的常数，复杂性可以简化为O（PNlogNlogS）。考虑到实际路网上从单个源点出发的最短路径的扩张是围绕源点的小网络，CCRP＋＋ 单次迭代的时间远小于CCRP。假设源点均匀分布在网络中，每个源点周围有N／S个节点，则CCRP的复杂性为O（PS（N／S）log（N／S）），即O（PNlog（N／S）），而 CCRP＋＋的复杂性为O（P（N／S）log（N／S）log（S）），即理论上CCRP＋＋是CCRP运算时间的log（S）／S。

4 实验分析

对算法CCRP＋＋和CCRP使用不同规模的路网数据进行测试。实验平台操作系统使用Windows XP 32bit SP3，配置CPU：Intel Core Duo T5500＠1.66GHz，内存1.5GB，编程语言使用C⧺。实验采用了3组规模不同的路网数据：第一组是由CCRP项目参与者Dr.Sangho Kim提供的CCRP实验数据SM，第二、三组数据是USGS发布的两个城市Oldenburg（OL）和San Joaquin（TG）的路网数据。根据网络规模，随机生成了疏散者人数、源点和目标点数。测试数据的属性如表2。

表2 不同网络下的测试数据Table 2 Test data in different network

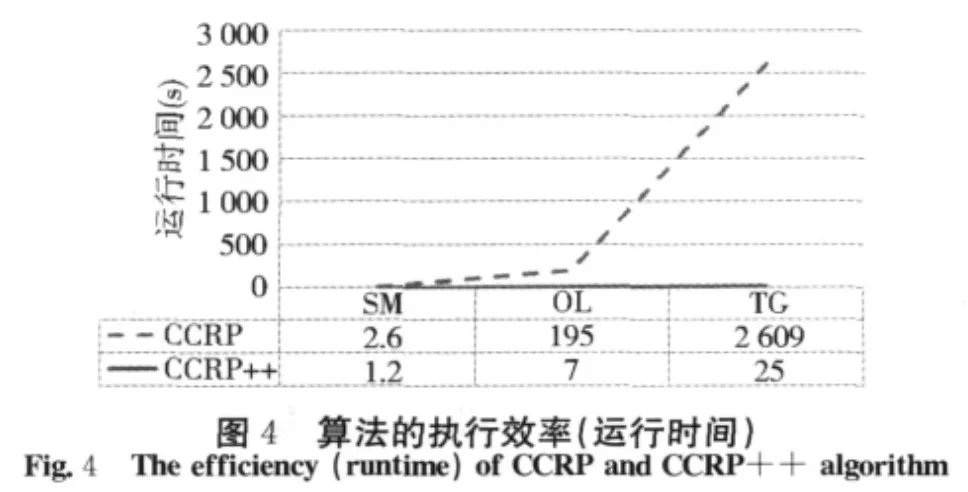
实验主要检测两种算法的效率和随网络规模的可扩展性。以整体运算时间和单次迭代运算时间进行测算。在整体运算时间上，CCRP＋＋相对于CCRP分别取得了2、28、100倍的加速（图4）；对比两种算法的单次迭代运算时间，CCRP的运算时间随网络规模增大、源节点数量的增多而明显增加，而CCRP＋＋的单次迭代运算时间几乎没有增长（图5）。这是因为无论有多少源点，每次都只进行一个源点的最短路径计算，少许的增量来自于进出两个优先队列PreRQ和RQ的代价，大小为O（logS）（S为源点数量）。实验表明CCRP＋＋在效率和可扩展性方面都优于CCRP。

5 结语

针对传统疏散算法CCRP的不足，提出了一种新型的启发式疏散算法CCRP＋＋，采用双优先队列结构，每次只更新一个源点的最短路径树，避免了CCRP每次迭代时进行所有源点的最短路径树更新，显著降低了算法的时间复杂度。真实路网的模拟实验表明，CCRP＋＋ 相比CCRP在算法效率和可扩展性上都有明显提升，这一改进有助于疏散算法在实际应急指挥系统的应用。

［1］ BAUMANN N，SKUTELLA M.Solving evacuation problems efficiently－earliest arrival flows with multiple sources［A］.47th Annual IEEE Symposium on Foundations of Computer Science［C］.2006.FOCS＇06.399－410.

［2］ HAMACHER H W，TJANDRA S A.Mathematical Modeling of E－vacuation Problems：A State of the Art［R］.Reports of the Fraunhofer Institute for Technological and Industrial Mathe－matics（ITWM Report），2002，24，227－266.

［3］ HPPPE B，TARDOS E.Polynomial time algorithms for some evacuation problems［A］.5th Annual ACM－SIAM Symposium on Discrete Algorithms［C］.Arlington，VA，1994.433－441.

［4］ LU Q，HUANG Y，SHEKHAR S.Evacuation planning：A capacity constrained routing approach［J］.Intelligence and Security Informatics，2003，2665：111－125.

［5］ LU Q，GEORGY B，SHEKHAR S.Capacity constrained routing algorithms for evacuation planning：A summary of results［A］.Proc.of 9th International Symposium on Spatial and Temporal Databases［C］.2005.291－307.

［6］ SANGHO K，GEORGE B，SHEKHAR S.Evacuation route planning：Scalable heuristics［A］.15th ACM International Symposium on Advances in Geographic Information Systems［C］.Seattle，WA，2007.1－8.

［7］ AHUJA R K，MAGNANTI T L，ORLIN J B.Network Flows：Theory，Algorithms，and Applications［M］.Prentice Hall，1993.

［8］ CAI X，KLOKS T，WONG C K.Time－varying shortest path problems with constraints［J］.Networks，1997，29（3）：141－149.

［9］ CHABINI I.Discrete dynamic shortest path problems in transportation applications：Complexity and algorithms with optimal run time［J］.Transportation Research Record，1998，1645（1）：170－175.

［10］ CHALMET L，FRANCIS R，SAUNDERS P.Network models for building evacuation［J］.Fire Technology，1982，18：90－113.

［11］ CHEN Y.Evacuation model and algorithms for emergency management system［A］.International Conference on Transportation Engineering［C］.2007.3171－3177.

［12］ KISKO T，FRANCIS R.Evacnet＋：A computer program to determine optimal building evacuation plans［J］.Fire Safety，1985，9（2）：211－222.

［13］ 尹大朏，方裕.应用于大规模灾害发生时进行人员疏散的快速疏散方法［P］.专利授权号ZL 2010 1 0279504.3.

［14］ 方裕，周成虎，景贵飞，等.第四代GIS软件研究［J］.中国图象图形学报，2001（6）：817－823.

［15］ 姜云昭，朱万红，邱国庆.地震次生灾害影响条件下人员疏散问题的研究［J］.中国安全生产科学技术，2008（1）：38－41.

［16］ 孔祥春.考虑交叉口延误的交通紧急疏散研究［D］.天津大学，2007.

［17］ 潘忠.基于几何的人员疏散仿真研究［D］.同济大学，2007.

［18］ 谢旭阳，任爱珠，周心权.高层建筑火灾最佳疏散路线的确定［J］.自然灾害学报，2003，12（3）：75－80.

［19］ 张江华，曹悦，朱道立，等.危险化学品事故应急疏散决策系统设计［J］.科技导报，2005，25（7）：47－51.

［20］ 何淑华，冯敏，陈伟玲.城市地震应急疏散规划编制研究——以《淄博市中心区地震应急疏散规划》为例［J］.城市规划，2008（11）：1－4.