变电站噪声预测和仿真分析
李永明 ,王玉强 ,徐禄文,沈婕
(1.输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆市 400044;2.重庆市电力科学试验研究院,重庆市 401123;3.重庆市电力公司市区供电局,重庆市 400014)
0 引言
随着我国电网建设的快速发展及人民生活水平的提高,城区用电负荷激增,越来越多的变电装置不可避免地进入城市。与此同时,一些偏远地区的变电站也开始被新城区所包围[1],变电站在运行过程中会产生不同程度的噪声,当噪声超过一定限制标准就会影响到人们正常的生活和工作,因此,变电站的噪声成为了人们日益关注的焦点。变电站内的噪声包含变压器本体的电磁噪声、冷却风机的机械噪声、变压器油冷却系统的液体流动动力噪声、设备运行中由电磁变化和机械运动产生的振动噪声等[2-4]。故变电站内的主要噪声是中低频噪声,人耳对其较为敏感,因此受到了越来越多居民的投诉。为了研究变电站的环境噪声影响问题,本文首先利用声级计对变电站站界及变压器周围进行了噪声测量,然后利用灰色理论的GM(1,1)模型对1个月内的噪声进行了预测;并利用径向基函数(radical basis function,RBF)神经网络预测了随温度、距离变化的噪声值,然后对不同温度和变压器负荷时的噪声进行了预测。
1 变电站的噪声源及其特点
变电站噪声源主要包括变压器、电抗器、电容器和配电装置的电磁噪声、进出线的电磁噪声和放电噪声[5]。影响变电站站内环境和站界噪声的主要噪声源是变压器[6]。当声源本身的长度远小于声源到受声点(敏感点)的距离,即声源至受声点的距离大于声源长度的3倍时,可以将声源看作一个点声源[7]。变电站的噪声以变电器铁心噪声为主,铁心噪声的频谱通常为100~500Hz。对于不同容量的电力变压器,铁心噪声频谱有所不同,额定功率越大,基频所占比例越大,谐频分量越小。
变压器噪声属于低频噪声,而且频率单一,易引起人的反感,从噪声控制的技术角度看,噪声频率越低,距离衰减率越低,吸收率越低,其治理难度越大[8]。
2 灰色预测模型
2.1 基本GM(1,1)模型
基本GM(1,1)模型[9]的建模步骤如下。
(1)设原始数据数列为

(2)对原始的数据作一次累加生成,生成新的数据列x(1):
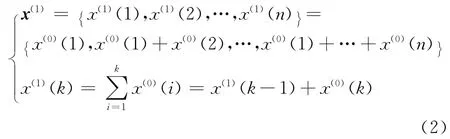
(3)GM(1,1)模型相应的微分方程为
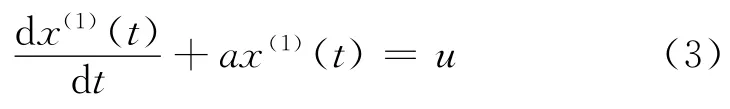
式中:a为发展灰数;u为内生控制系数。
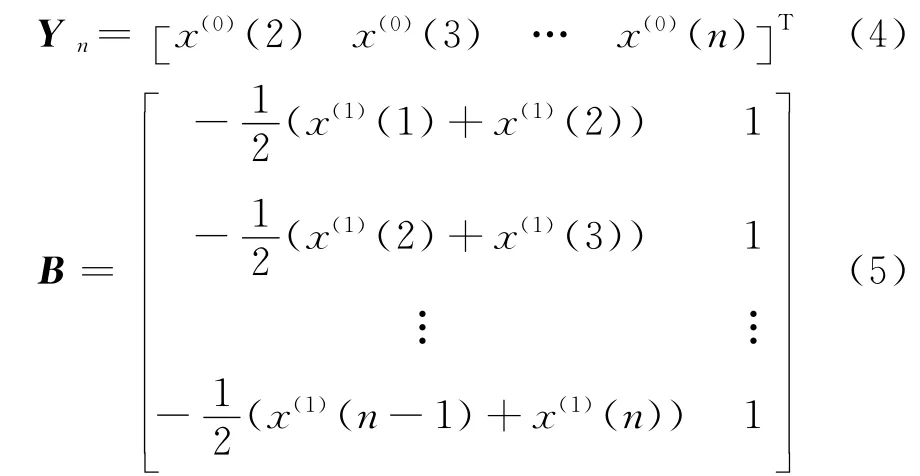
(5)利用最小二乘法求解系数:

(6)求解GM(1,1)方程,得到其对应的时间响应函数,即为GM(1,1)白化预测模型解:
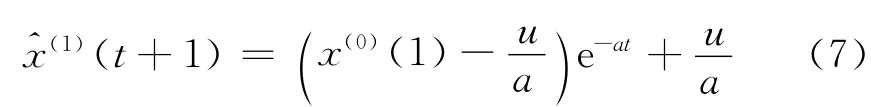
(7)对一次累加生成数列的预测值进行一次累减生成,得到原始数据的还原预测值,即
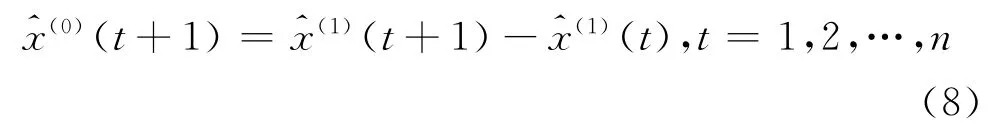
2.2 无偏的GM(1,1)模型

(1)设原始序列为
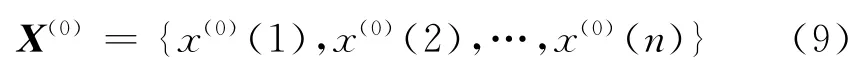
(2)累加生成:对X(0)作一次累加生成序列
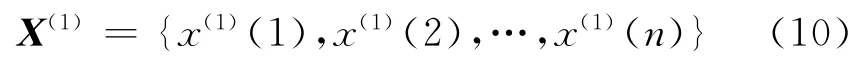
(3)求背景值:

(4)确定数据矩阵B、Y:对a*=[a,b]T进行最小二乘估计a*=[a,b]T=(BTB)-1BTY,其中:

(5)求无偏GM(1,1)模型参数:

(6)建立原始数据序列模型:

3 RBF神经网络预测模型
RBF神经网络是一种3层前向网络[10-11]:首先利用径向基函数作为隐含层节点的“基”构成隐含层空间,对输入矢量进行一次变换,将低维模式的输入数据映射到高维空间内,然后通过对隐含层结点输出的线性加权求和得到输出,即通过线性函数将隐含层节点的输出映射到输出层节点空间,这就是RBF网络的基本思想。
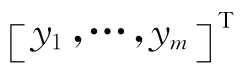
4 变电站可听噪声预测分析
4.1 可听噪声数据样本

图1 RBF神经网络结构模型Fig.1 RBF neural network model
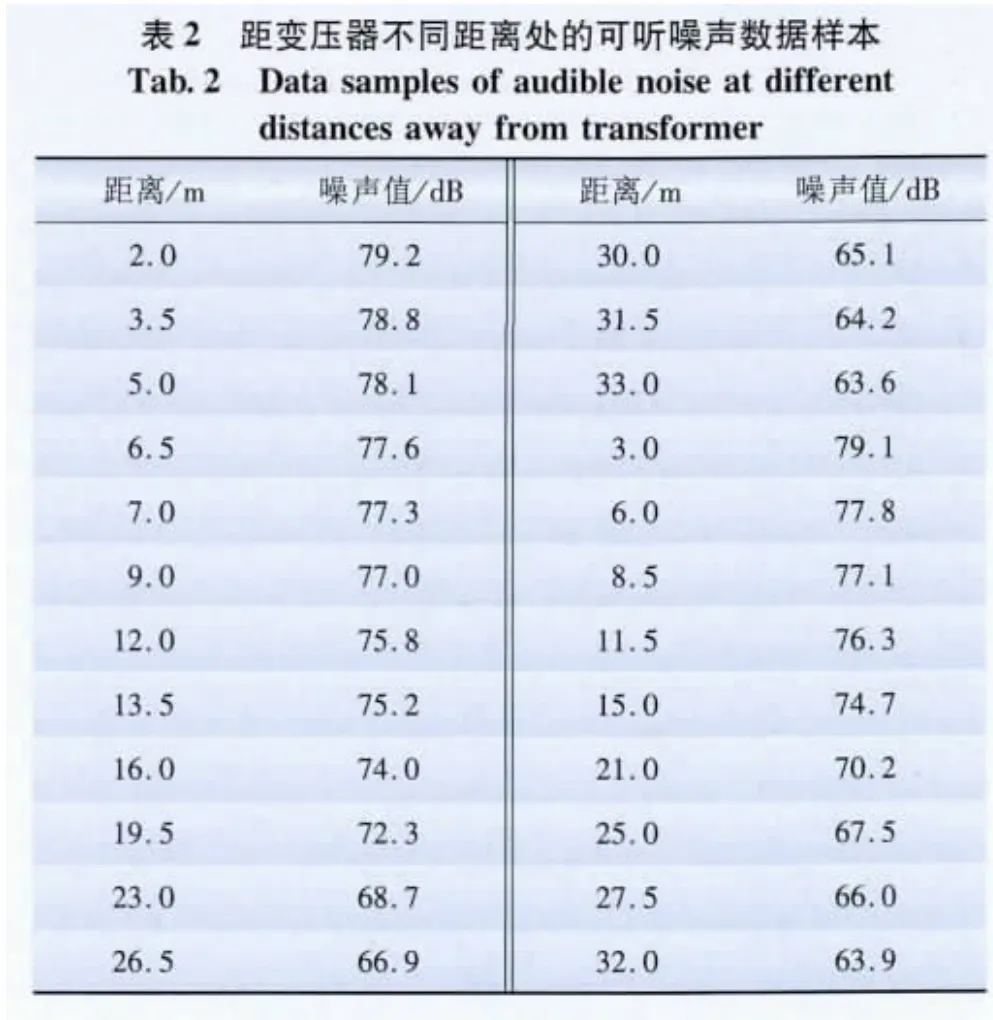
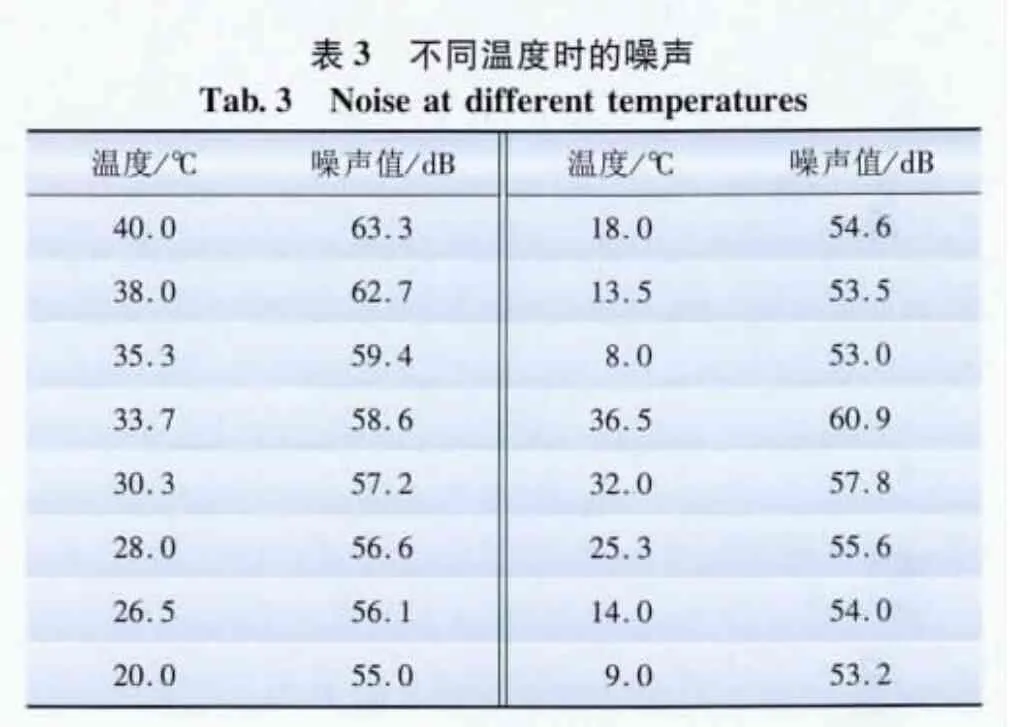
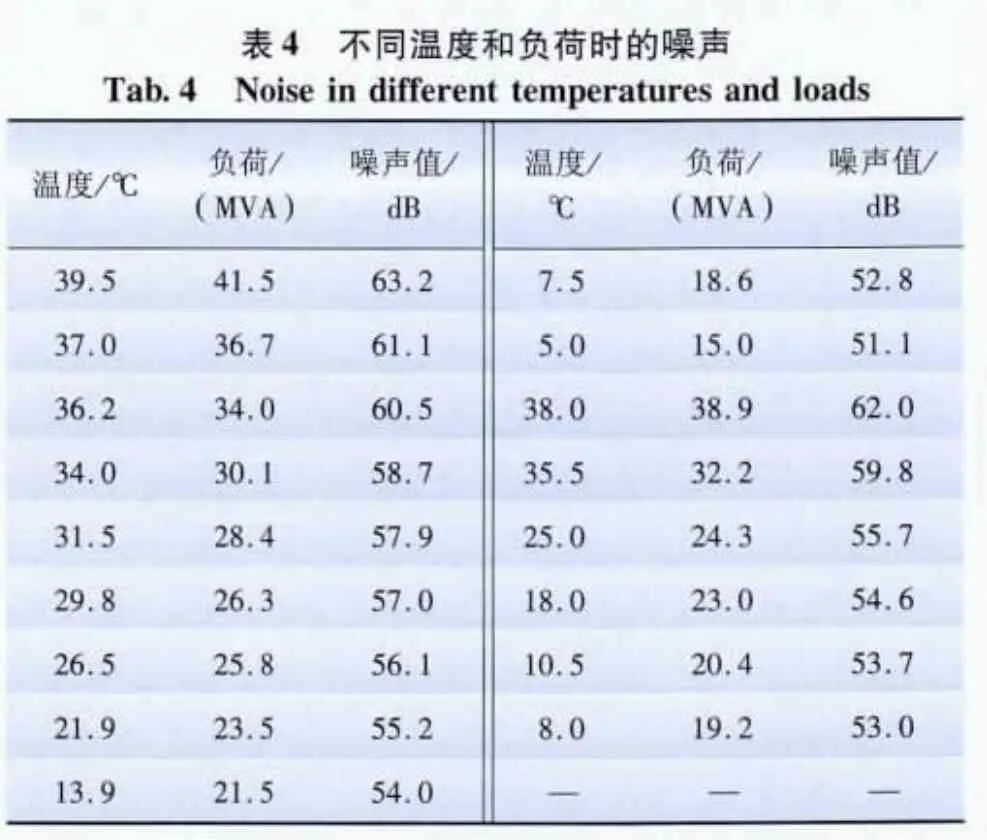
本文对重庆和尚山110kV 变电站进行了全时段、宽频带噪声监测,表1为11月份晚上12点的噪声数据,选定该月份的噪声数据主要是因为11月份环境条件比较稳定,温度大约都是15℃左右,变压器的运行负荷相差不大。表2为测量的距变压器不同距离时的噪声值,不同温度下的噪声如表3所示,不同温度和负荷时的噪声如表4所示。
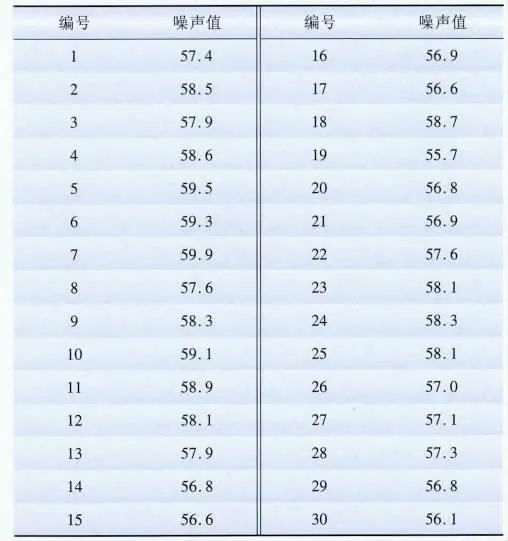
表1 变电站可听噪声数据样本Tab.1 Data samples of substation's audible noise dB
4.2 变电站可听噪声的预测分析
4.2.1 噪声预测分析
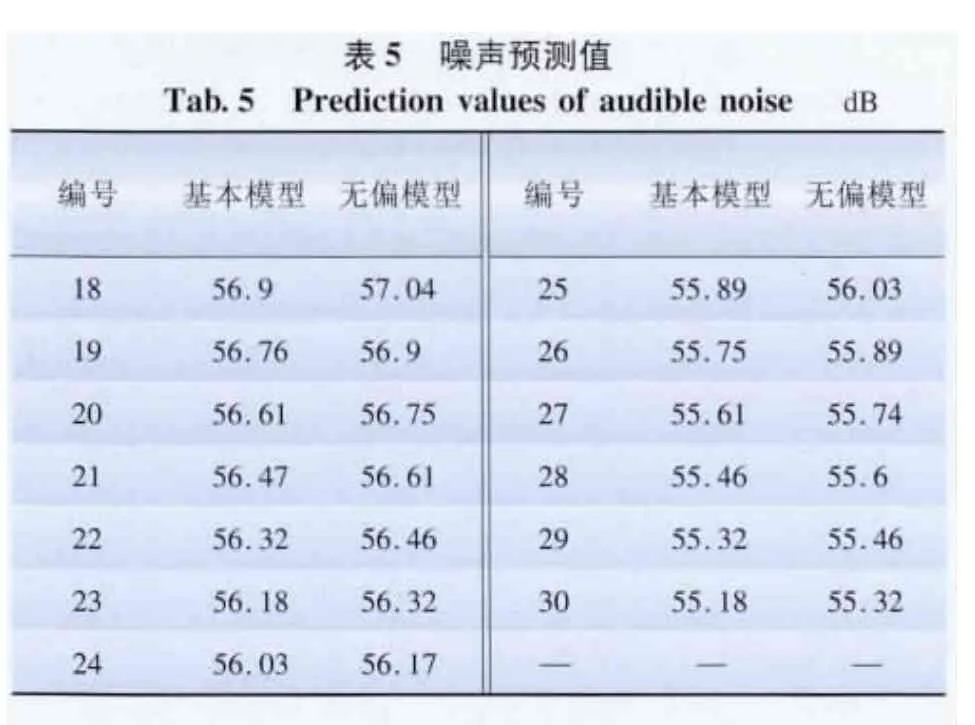
本文利用表1中数据样本的前17组数据进行训练,后13组数据进行检验。其预测结果如表5所示。
图2所示为预测值的相对误差,从图2 可以看出,预测模型的误差都很小,基本GM(1,1)模型预测的最大相对误差为3.894%,其平均相对误差为2.426%;无偏GM(1,1)模型预测的最大相对误差为3.654%,平均相对误差为2.221%。故GM(1,1)模型可以用来对变电站的噪声进行预测。因为噪声的大小和负荷、温度有关系,预测时应根据实际情况进行分类,最好对每个月的噪声情况分别进行预测,之后建立典型的噪声数据库,为以后建立变电站提供参考。

4.2.2 噪声随影响因素变化的计算分析
利用RBF神经网络中的工具箱函数newrbe(P,T,spread)方法对表2中的前15组数据进行训练,后9组数据进行验证分析,其预测结果如图3 所示,预测误差见表6。同样的方法对表3中的前11组数据进行训练,其预测结果如表7。同样对表4中的前11组数据进行训练,后6组数据进行检验,其预测结果如图4所示。
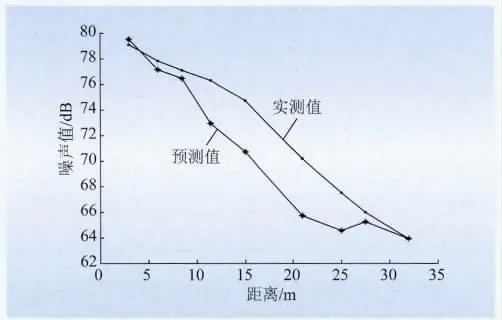
图3 距变压器不同位置处的噪声预测值Fig.3 Prediction results of audible noise at different positions away from transformer



图3为距变压器不同位置处的噪声预测值,从图3可以看出其预测效果很好,从表6可以看出,其最大平均误差为5.368%,可以用来进行预测分析,并且通过计算可以得到变电站内的噪声分布。图4为变压器不同运行负荷条件下的噪声分布情况,其预测结果很好,其中,newrbe()方法的噪声预测结果更好,其最大相对误差为0.398 7%。从表7也可以看出,对不同温度的噪声预测比较准确,最大相对误差是2.52%。因此,通过预测分析可以得知噪声随季节温度的变化情况,为相应时期的噪声控制提供参考。
5 结论
(1)通过无偏的GM(1,1)模型可以优化预测结果,利用该模型对实例的噪声进行了预测,其最大相对误差为3.654%,平均相对误差为2.221%。可以用来对变电站的噪声进行预测,针对不同月份的噪声分别进行预测分析,然后建立典型的噪声数据库,为以后建立变电站提供借鉴。
(2)利用RBF神经网络对不同温度、负荷和距离时的噪声进行了预测,预测结果很好,可以用来进行预测分析,进而得到噪声的分布情况。
[1]叶建斌,陈雁.变电站环境噪声现场测试与讨论[J].广东电力,2005(10):53-56.
[2]李冰,胡国清.降低变压器噪声的措施初探[J].变压器,2004(8):40-42.
[3]周贤士.中小型变压器噪声(上)[J].变压器,2006(11):1-9.
[4]肖冰,徐迪.750kV 变电站噪声预测及防治[J].电力建设,2012,33(6):30-33.
[5]侯婷.绿色变电站的电气设计[J].电力建设,2012,33(5):45-48.
[6]郭天兰.220kV 变电站噪声水平分析及控制措施[J].山西电力,2011,4(2):7-10.
[7]国家环境保护总局.HJ/T 90—2004声屏障声学设计和测量规范[S].北京:中国环境科学出版社,2004.
[8]刘嘉林,王毅.城区箱式变压器环保监测分析与安装建议[J].城市管理与科技,2005,7(5):198-199.
[9]罗晓玲,周建新,王玉兰.基于GM(1,1)模型在高等学校招生人数预测中的应用研究:以四川省普通高校为例[J].贵州大学学报:自然科学版,2008,25(4):342-345.
[10]陈以,万梅芳.RBF神经网络在物流系统中的应用[J].计算机仿真,2010,27(4):159-162.
[11]魏海坤.神经网络结构设计的理论与方法[M].北京:国防工业出版社,2005:40-41.

