电梯永磁同步门机速度环的H∞控制器
曹 歆,忻 谊
(上海三菱电梯有限公司,上海 200245)
0 引言
据统计,电梯的门机故障占电梯所有故障的70%左右,因此,提高门机的稳定性和可靠性是提高电梯性能的重要手段之一。根据不同需求,门机有许多规格,其控制系统的内部参数存在一定的变化范围。门机在运行过程中也受到外界扰动,如导轨变形、异物阻塞等情况产生的阻力。这些因素都将影响门机的动态性能和稳定性。在设计门机控制系统时,通过基于鲁棒的设计可以提高门机运行的稳定性和可靠性。
1 系统建模
永磁同步电机已经十分广泛的运用于电梯的门机系统中,其电气控制系统一般采用id=0 的双闭环矢量控制方法,系统框图如图1所示。
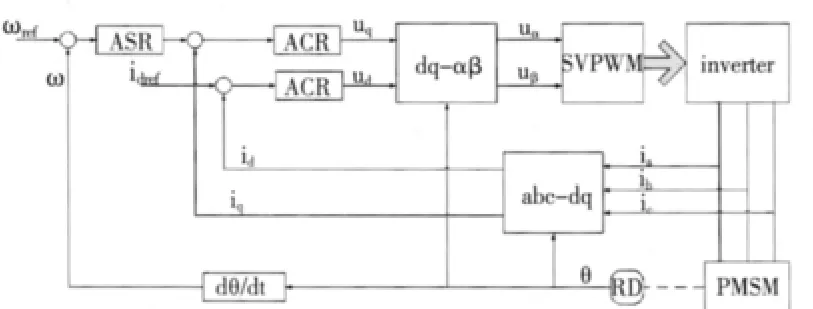
图1 永磁同步门机电气控制系统框图
该控制系统由速度环控制器、d 轴和q 轴的电流环控制器、坐标变换、脉宽调制、逆变装置、永磁同步电机、速度和位置反馈模块组成。
根据一款电梯门机控制器的参数,在Matlab 中建立其模型。其中速度环控制器(ASR)为PI 控制器,参数设定为:Integral=7,Proportional=0.52。d 轴和q 轴的电流环控制器(ACR)也为PI 控制器,两个控制器的参数都设定为:Integral=5875,Proportional=4.5。
在系统框图中有2 个坐标变换过程,分别是(d-q)至(α-β)和(a-b-c)至(d-q)。永磁同步电机的模型的输出端可以直接引出id和iq,(d-q)至(α-β)的变化模块可由一个简单的函数定义。脉宽调制选用SVPWM 空间矢量脉宽调制方法。逆变器模型可将Universal Bridge 模块和DC Voltage Source 模块联接起来。永磁同步电机的模型可以直接调用,参数如下:
定子电阻(折算至d-q 坐标系)R=31.86Ω,定子电感(折算至d-q 坐标系)L=20.1mH,转子转动惯量J=3.35×10-4kgm2,极对数p=8,转子磁通Φf=0.4083Wb。
根据系统图选取转子转速ω,转子位置θ,d 轴电流id和q 轴电流iq作为输出量,同时选取电磁转矩Te连接示波器,可直观的了解电机的运行情况。不考虑门倾斜时的水平分量,在开门过程中:

式中:Fm—电机的驱动力;m—层门和轿门的总质量;f—估算的摩擦力;Fzc—层门重锤的强迫关门力;r—输出轴轮槽半径。按常用规格,m=220kg,Fzc=49N,f=4.9N,r=0.0218m。根据式(1)作出门扇负载的模型。
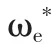

图2 转速、电磁力矩、Id、Iq曲线图
2 门机运行的混合灵敏度问题
在电梯门机的运行过程中,有许多影响控制系统正常运行的扰动量。大体有:联动装置间隙过大产生的振动;门导靴在地坎或门滑轮在导轨上受到的摩擦力或阻力;同步带或钢丝绳张紧力下降导致松弛下垂;门扇变形,在运行过程中与轿厢前壁发生摩擦;各个层站层门的材质或高度可能各不相同,导致门扇质量有所不同。
由于导轨变形、门扇变形、地坎阻塞等因素导致摩擦力和阻力突然增加,这些不确定负荷是加载在电机控制系统输出端的外部干扰。电机模型是在许多假设条件下建立的,与实际值有一定的误差;不同规格的门扇重量使得整个系统的内部惯量有所变化;同步带、钢丝绳的张力松弛导致传动效率降低,这些因素使控制系统内部在实际运行时存在参数摄动。根据上述情况,可将控制器的设计转化为混合灵敏度问题,运用H∞控制的标准问题的方法加以求解。
3 速度环H∞控制器的设计
3.1 永磁同步门机系统的数学模型
表面式永磁同步电机在id=0 控制方法时的(d-q)坐标系下的电压、磁转矩和运动方程如下:
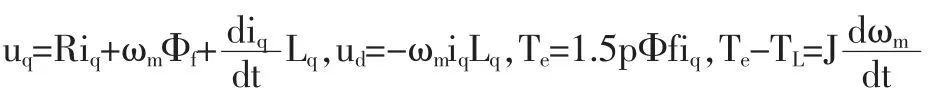
式中,ud、uq—定子电压d、q 轴分量;iq—定子电流q 轴分量;Lq分别为q 轴电感分量;Φf—永磁体的等效磁通,ωm 为转子电角速度,R 为定子绕组的电阻,p为极对数。
设:KT—转矩系数:KT=1.5pΦf;Kω—电势系数:Kω=pΦf;Ki—电流反馈系数,取Ki=R;KACR为电流环控制器的增益,KACR=4.5。得出其动态结构框图如图3所示。
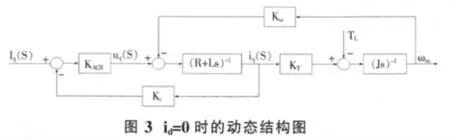
其传递函数G(s)为:
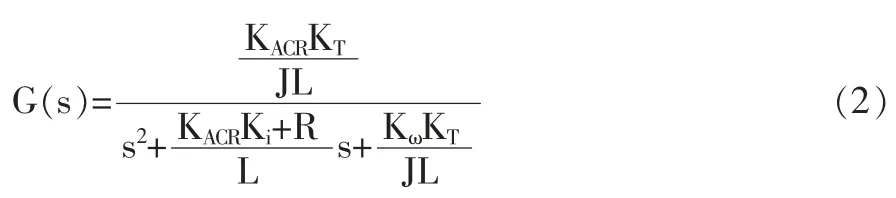
按照永磁同步电机的参数值,代入式(2):
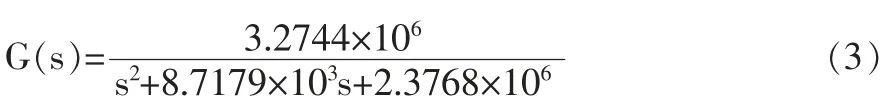
3.2 在Matlab 中设计H∞控制器
(1)设G 为标称对象,根据G 的传递函数,设置参数num 和den,并用tf 函数生成其模型:G=tf(num,den)。
(2)用tf2ss 函数将传递函数转换为状态空间模型:[a,b,c,d]=tf2ss(num,den)。
(3)用mksys 函数将状态空间模型转换为单独的S模型变量:S=mksys(a,b,c,d)。
(4) 赋值加权函数W1、W2、W3。
(5)用augtf 函数生成广义对象P=augtf(S,W1,W2,W3)。
(6)设F(s)为H∞控制器,用函数hinf () 设计H∞控制器。调用格式为:[ss_f,ss_cl]=hinf(P)。其中,P 为广义对象。返回变量中,ss_f 为H∞控制器F(s)的树变量形式,ss_cl 为F(s)作用下的闭环系统状态方程的树变量形式。
在求解前,Matlab 首先验证H∞控制器存在的所有前提条件是否满足:①控制器Riccati 方程的解X 为正定矩阵;②观测器Riccati 方程的解Y 为正定矩阵;③两个Riccati 方程的积矩阵的所有的特征值均小于γ2,即λmax(XY)<γ2。若不满足前提条件,则需要重新调整加权函数W1、W3,如此循环,直至所有条件满足,则将设计出一个H∞控制器。
(7)当满足上一步后,用hinfopt () 函数来求得最优H∞控制器。该函数使用了二分算法来实现迭代过程,调用格式为:[g,ss_f,ss_cl]=hinfopt(P)。其中,g 为最优的γ 值,其它变量同hinf () 函数。
(8)用branch 函数提取求得的H∞控制器树变量中的组成变量:[af,bf,cf,df]=branch(ss_f)。
(9) 用ss 函数将H∞控制器转换成状态空间:F=ss(af,bf,cf,df)。
(10) 用tf 函数将H∞控制器转换成传递函数形式:F_t=tf(F)。或用zpk 函数转换成零极点形式:F_z=zpk(F)。
在H∞优化设计中,加权函数的选择是十分重要的一步,直接反映了系统的各种性能指标要求。按照选择加权函数的原则,同时满足H∞控制器存在的所有条件,经多次调整后选取:

3.3 H∞控制器时的永磁同步门机系统仿真
将计算出的H∞控制器F(s)的分子上增加一个极小的微分环节(0.000001s+1),在不影响特性的基础上,使F(s)的分子与分母同阶,即:F'(s)=(0.000001s+1)F(s),用F'(s)模块代替模型中的速度环PI 控制器,然后进行仿真。
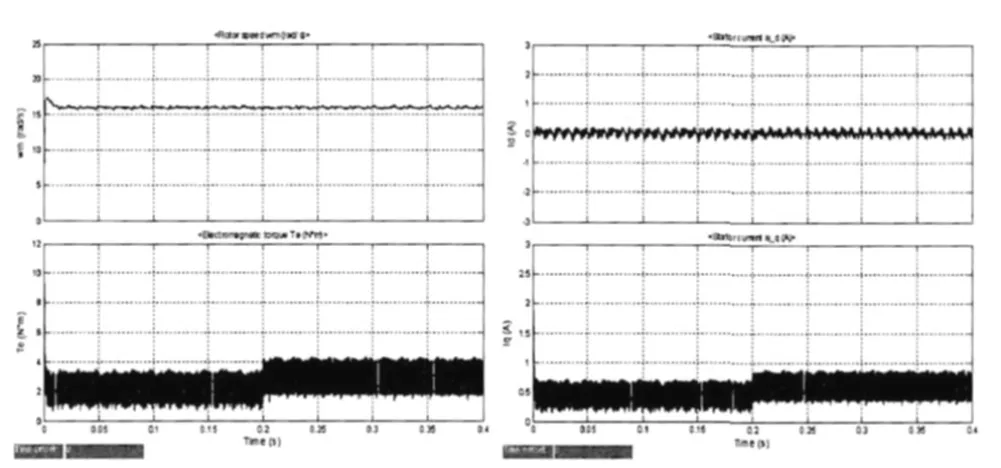
图4 H∞控制时,转速、电磁力矩、Id、Iq曲线图
仿真试验的条件与PI 控制器时相同,结果如图4所示。对照速度环为PI 控制器时的仿真结果,可以得出:H∞控制时,启动时的转速ωm响应比PI 控制时快,但有微小的超调。负载突增时,H∞控制的转速ωm没有下降迹象,说明系统具有很强的抗扰性。
将系统的参数:转子转动惯量J、定子电阻R、定子电感L 和磁通Φ 各增减15%左右,模拟系统参数的摄动。经过仿真实验,三种情况下的门机系统输出的转速ωm基本上重合在一起,没有明显偏离和变化,表明该H∞控制器对参数摄动也有很强的鲁棒性。
4 总结
将H∞控制器代替门机控制系统速度环的PI 控制器,对负载扰动和参数摄动两方面情况下的系统进行了仿真实验。仿真结果表明:在H∞控制器作用下,负载突增和在参数摄动时,转速基本没有明显变化,该控制系统具有较强的抗扰性。
[1]刘鸿皓,等.永磁同步电动机速度控制方案[J].电气传动,2006,2.
[2]黄曼磊.鲁棒控制理论及应用[M].哈尔滨:哈尔滨工业大学出版社,2007.
[3]张静.MATLAB 在控制系统中的应用[M].北京:电子工业出版社,2007.
[4]翁旦.电梯门机系统的实验研究和性能分析[D].上海:上海交通大学,2008.
[5]GB7588-2003.电梯制造与安装安全规范[S].

