低温条件下冷却猪肉中假单胞菌生长模型的比较分析

牛会敏，李苗云*，赵改名，张秋会，田 玮，黄现青，柳艳霞，张建威，高晓平，孙灵霞

(河南省肉制品加工与质量安全控制重点实验室，河南农业大学食品科学技术学院，河南 郑州 450002)

近年来，冷却猪肉逐渐发展成为我国生鲜肉消费的主流，国内外关于冷却猪肉中假单胞菌生长预测模型已经做了大量研究[1-4]。在预测微生物学领域，修正的Gompertz、Baranyi、Logistic及Huang等初级模型常被用来描述微生物数量随时间的变化关系，在已有的研究中，大都选用单一的模型来描述假单胞菌数量随时间变化的函数关系。尽管很多不同的非线性方程被当做模型用来预测微生物的生长，但并不能确定哪一种模型可以在本质上更优于其他模型[5]。在模型选择上很多学者做出了相当多得努力，一些比较研究文献也有报道[6-9]，然而有必要直接采用以实际食品为培氧基质而培养的微生物数据来评价常用初级模型的统计拟合能力。

本实验选择3种常用的初级模型来拟合由冷却猪肉复杂微生物体系中直接测定的假单胞菌生长数据，用残差值分布图及残差平方和(residual sum of squares，RSS)，残差标准误(residual standard error，RSE)及赤池信息量准则(akaike information criterion，AIC)等统计指标来综合比较分析3种模型拟合托盘包装冷却猪肉中假单胞菌生长的情况，为冷却猪肉假单胞菌预测预报体系模型选择提供理论指导。

1 材料与方法

1.1 材料与试剂

冷却猪肉猪背最长肌 河南漯河双汇集团。

假单胞菌琼脂(CM0559、SR0103E，PE真空包装袋) 英国Oxoid公司。

1.2 仪器与设备

HVE-50压力蒸汽灭菌锅 日本Hirayama公司；SPX-1505H-Ⅱ生化培养箱 上海新苗医疗器械公司；SW-CJ-2F洁净工作台 苏州安泰空气技术有限公司；MIR-254 低温恒温培养箱 日本Sanyo公司；VORTEX-2 GENIE 涡旋振荡器 美国Scientific Industries公司。

1.3 方法

1.3.1 取样及贮藏

从双汇集团分割生产线随即采取猪背最长肌，用保鲜膜包裹，放置装有冰袋的保温箱中，迅速转运至实验室。修去筋腱后，将肉无菌切成小块，按质量称取每袋220g左右进行真空包装，在0、5、10℃条件下贮藏。贮藏在0℃条件下的冷却猪肉，每隔48h取样测定假单胞菌；5℃贮藏的样品每隔24h取样测定；10℃贮藏的样品每隔12h取样测定。

1.3.2 冷却猪肉中假单胞菌的计数方法

无菌操作称取25g样品，用剪刀剪碎后置于装有225mL的8.5%灭菌生理盐水的锥形瓶中，充分振摇，取100μL按1：10进行倍比稀释，之后按照修改的6×6点样法[10]进行微生物测定。每组样品做5次平行。

1.3.3 微生物生长动力学模型

在预测微生物学领域，预测模型是按数学模型进行分类的，初级模型表征的就是在一定生长环境和条件下微生物数量随时间变化的关系。选择3种常用的初级模型来拟合低温条件下冷却猪肉中假单胞菌的生长数据。

修正的Gompertz模型是经验模型，最初不是设计用来描述微生物生长，只是模型中的参数被赋予了物理含义来解释微生物的生长参数，而这些参数在建立和解释模型时都发挥了重要作用，此模型因使用简单而被广泛应用于预测微生物的生长。为了直接与另外两个生物学基础的模型进行比较，本实验用自然对数值取代常用对数值，修正的Gompertz模型直接表述为：

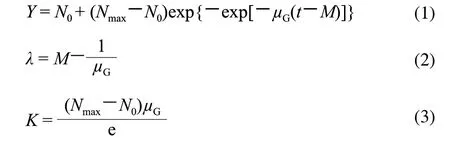
式中：Y是t时微生物的自然对数值(ln(CFU/g))；Nmax和N0分别是Y的初始值、最大值；μG是在时间M时的相对最大生长速率；M是达到相对最大生长速率所需要的时间。恒温条件下迟滞期λ和生长速率K可根据公式(2)、(3)计算。

由Baranyi等[11]在1994年提出的Baranyi模型得到了越来越广泛的应用，其最大的优点就是拟合性较高，并且使用方便；动态环境也可以使用；适合多种情况；模型中的参数都具有生理学意义，是真正意义上的动力学模型。其方程描述如下。

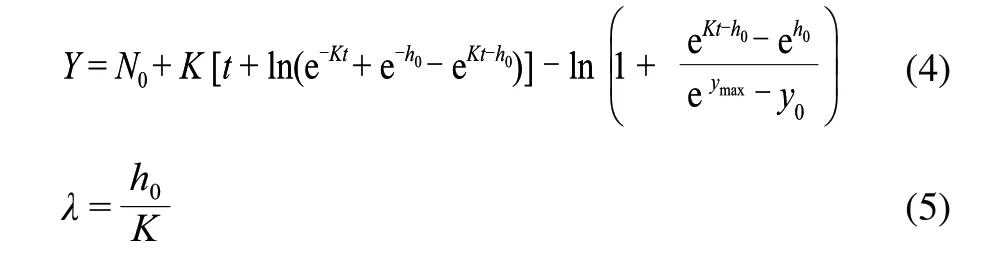
式中：N0和ymax分别是Y的初始值、最大值；K是生长速率。

迟滞期的计算根据公式(5)，参数h0只是使曲线拟合更适宜的原始数据的一个中间转换[12]。

最后选择的是Huang模型[13]，该模型来源于恒温条件下微生物生长情况的3个阶段(迟滞期、对数期、稳定期)，公式可以描述为式(6)、(7)。

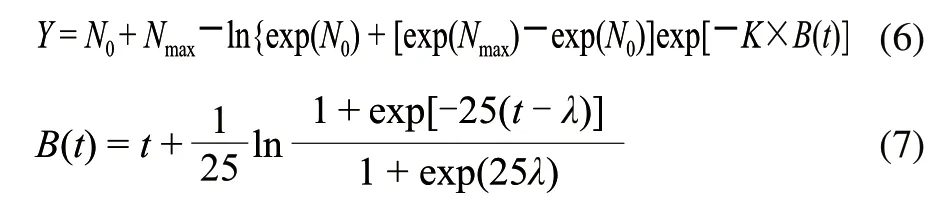
公式中参数的生物学意义同Baranyi模型。

1.4 数据分析

采用Excel分别计算每个样品假单胞菌数取对数值后的平均值[平均lg()][14]，每个样品假单胞菌取平均值后的对数值(N)，假单胞菌平均值的估计值(lgA)。

式中：k为lg菌落数；s为标准差。

采用SAS的统计软件对假单胞菌的生长数据进行非线性回归拟合。目前，并没有一个单独并简单的统计方法来评价非线性模型之间的异同及如何优先选择一个模型这个问题。一般情况下，主要选择残差分析和拟合度等统计标准来评价不同非线性模型之间的比较，从而综合评价模型的整体拟合能力[15]。本实验用残差分析、RSS、RSE及AIC来整体评价3种模型的拟合能力。RSS和RSE值越小，模型拟合效果越好。采用Excel软件对拟合的生长曲线进行绘图。

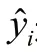
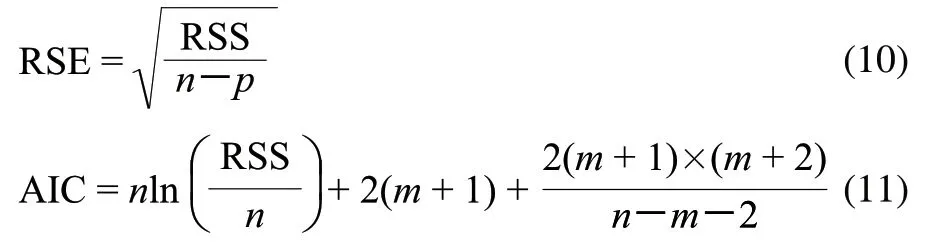
式中：n为实验数据的总数；p为模型中参数的个数；RSS为残差平方和；n为数据的总数；m为模型中参数的个数。AIC是衡量统计模型拟合优良性的一种标准，在不同的温度条件下对实验数据进行拟合，AIC值最小的模型是最准确的[16]。

2 结果与分析

2.1 低温条件下冷却猪肉中假单胞菌的生长特点

假单胞菌属是嗜冷菌，一直被认为是在有氧条件下引起冷却肉腐败的主导作用菌[17-18]。由图1可知，3组温度下假单胞菌的初始菌值分别是11.81(ln(CFU/g))、8.65(ln(CFU/g))和9.25(ln(CFU/g))，从迟滞期的细节图2可以明显看出，托盘包装冷却猪肉中假单胞菌在低温条件下(0、5、10℃)出现明显的菌数下降趋势，随后呈现典型“S”形生长。可能是样品经历了从企业到实验室的温度波动历程后，低温贮藏抑制了假单胞菌的生长，导致假单胞菌数量的下降。另外，假单胞菌是冷却猪肉屠宰过程中污染的微生物，在猪肉这种新环境适应过程中，细胞由于不适应新环境生长导致了死亡速率大于生长速率，从而出现了初始假单胞菌数量下降的趋势[19]。

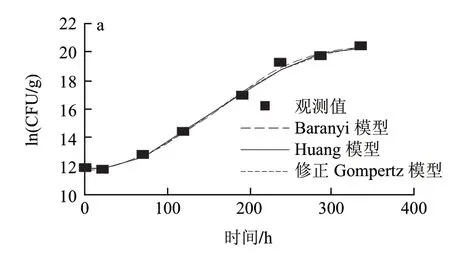
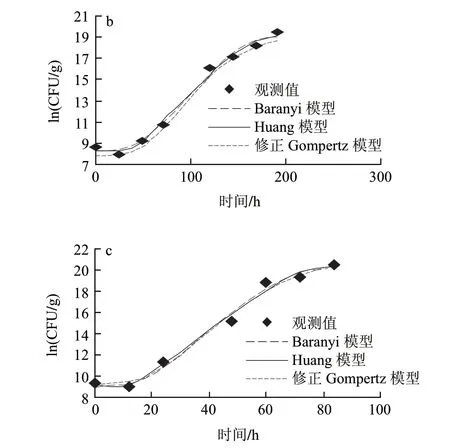
图 1 0(a)、5(b)、10℃(c)条件下冷却猪肉中假单胞菌观测值及拟合曲线Fig.1 Growth fitting curves of Pseudomonas in chilled pork at 0(a), 5 ℃(b) and 10 ℃(c)

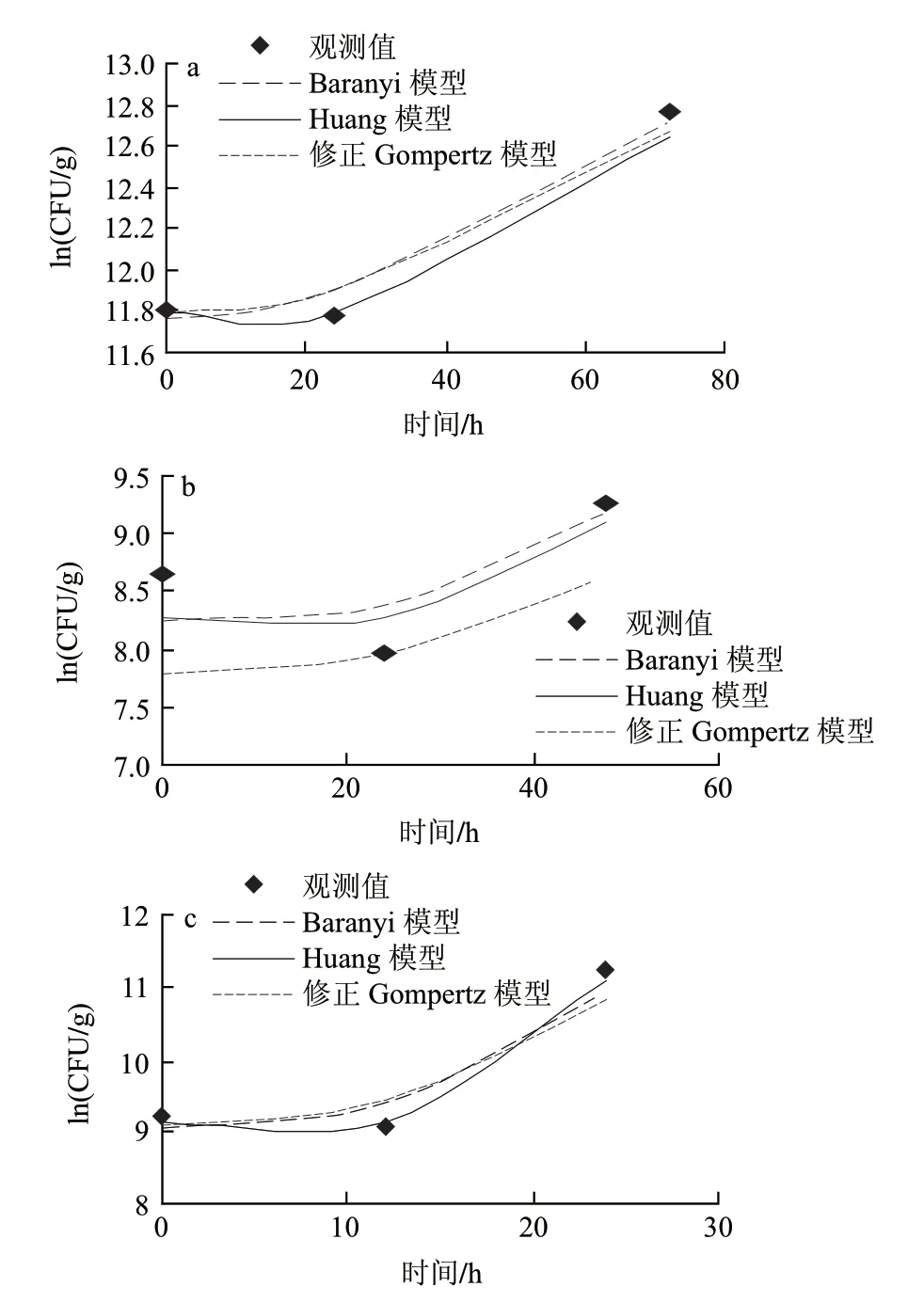
图 2 0(a)、5(b)、10℃(c)条件下冷却猪肉中假单胞菌迟滞期细节图Fig.2 lg phase of Pseudomonas in chilled pork at 0(a), 5 ℃(b) and 10 ℃(c)

2.2 3种模型统计指标的比较分析

2.2.1 残差分布的分析

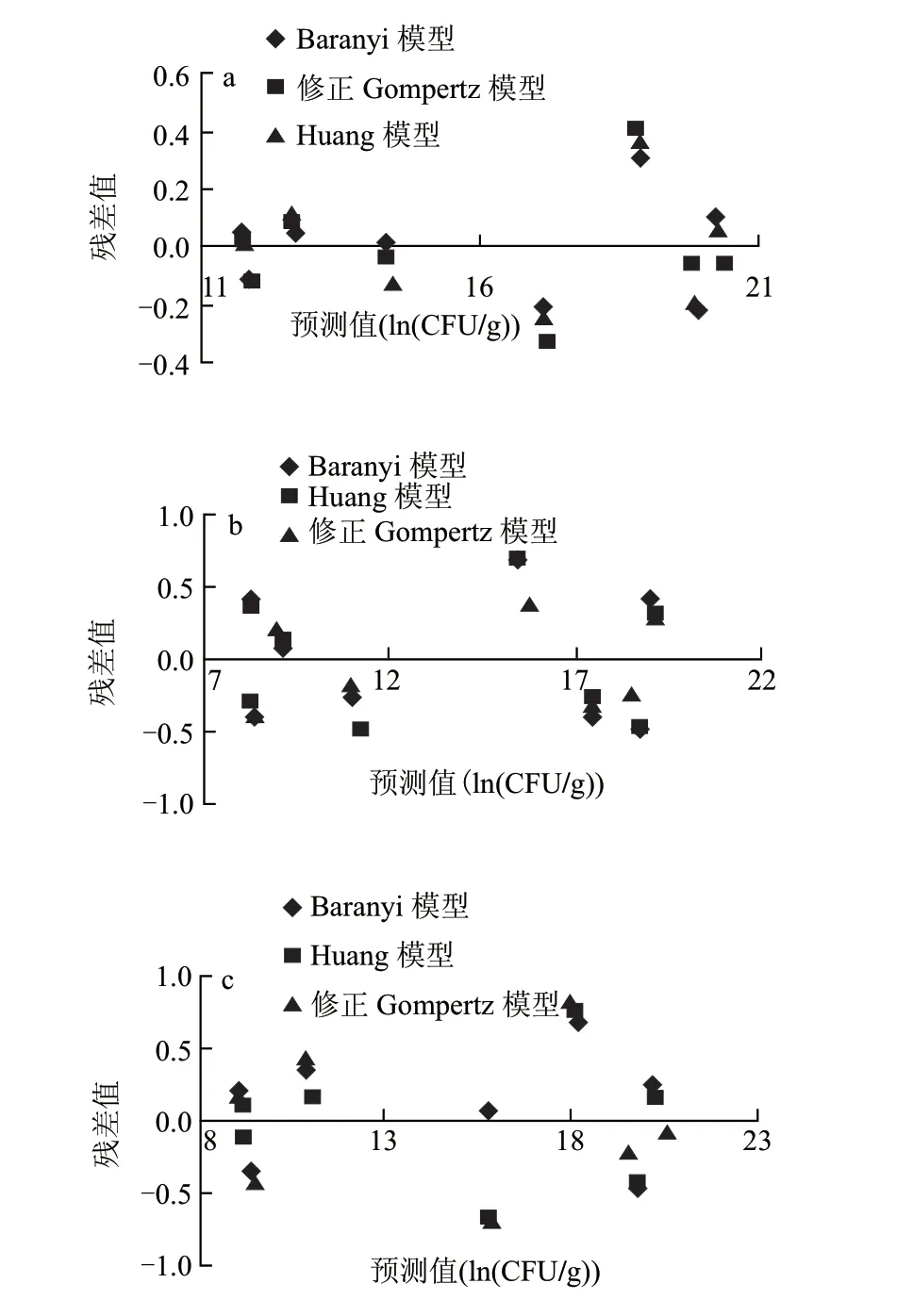
图 3 0(a)、5(b)、10℃(c)条件下3种模型拟合的冷却猪肉中假单胞菌数据的相对残差值分布图Fig.3 Distribution of relative residuals for three kinetics models for Pseudomonas growth in chilled pork at 0(a), 5 ℃(b) and 10 ℃(c)

由图3可知，在0℃条件下，3种模型的残差值均围绕残差等于零的直线上下随即分布，这说明回归曲线对原观测值的拟合情况良好。而相对于修正的Gompertz和Huang模型来说，Baranyi模型拟合的残差值分布更集中，在±0.3的范围内波动，说明在0℃条件下，Baranyi模型能更准确地预测冷却猪肉中假单胞菌的生长状况。在5℃条件下，修正的Gompertz模型拟合的残差值分布相对集中，在残差值等于零的直线上下随即分布，范围波动在±0.4以内，说明在此温度下，修正的Gompertz模型能更准确的预测冷却猪肉中假单胞菌的生长情况。同样的分析在10℃条件下，Huang模型是预测假单胞菌生长最准确的选择。

2.2.2 拟合度统计指标的分析

表1反映的是低温条件下3种模型拟合的统计指标的比较分析。可以看出，在0℃条件下，Baranyi模型拟合的RSS、AIC和RSE值是最小的，5℃条件下修正的Gompertz模型拟合的RSS、AIC和RSE值是最小的，而10℃条件下，拟合出最小RSS、AIC和RSE值的却是Huang模型，3种模型中的任何一个模型都不能同时对所有温度下的实验数据表现出最佳的拟合能力。Baty等[20]在5～42℃范围内的不同条件下，比较了修正的Gompertz、Baranyi和Lag-exponential模型对15个数据库里关于混合大肠杆菌O157：H7菌株生长数据的拟合情况，得出没有一个模型可以对所有的数据表现出持续的最佳拟合能力。

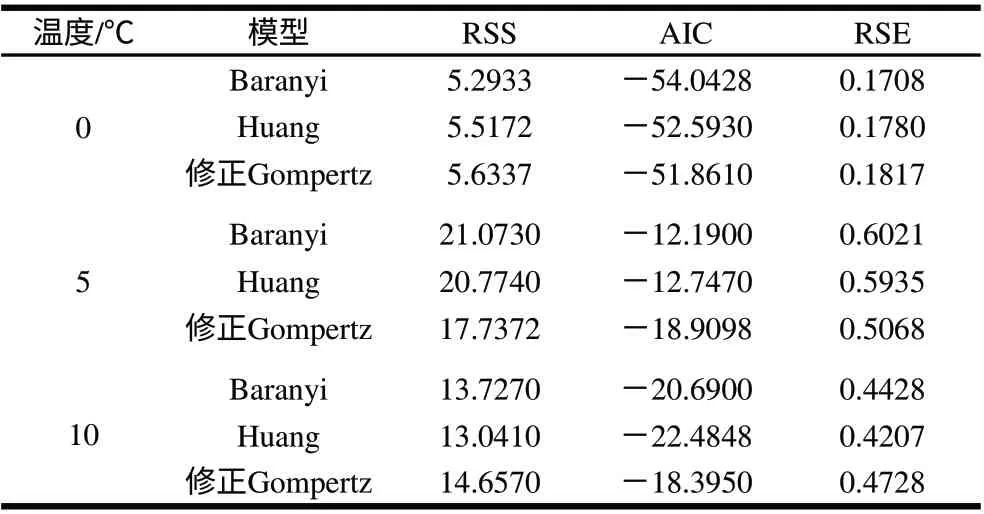
表 1 3种模型拟合的各项统计指标的比较分析Table 1 Comparative analysis of statistical parameters obtained from three growth models

目前国内外报道的研究中大多是采用单一的某一个模型对微生物进行预测，如杨红菊[21]、何帆[22]等均选用修正的Gompertz函数对不同包装方式冷却猪肉中的假单胞菌建立了动力学生长预测模型；Sivila[23]、Radovan[24]等使用Baranyi模型分别建立了有氧条件下生鲜禽肉中假单胞菌的生长预测模型。Koutsoumanis等[25]结合温度和pH值的影响使用Baranyi分别建立了猪肉和牛肉中假单胞菌的生长预测模型。

对于建立微生物预测模型的数据收集来说，用液体培养基培养与实际肉品不同，肉汤培养基体系稳定，不考虑原料组织对微生物的影响，大都采用确定的某一个模型进行建模；而实际肉品中微生物生长体系复杂，通过自然污染的原料肉直接测定的数据考虑了肉中复杂的微生物生长环境，能更真实的反映微生物的生长情况，因此有必要研究此环境下的微生物生长预测模型。

目前肉中假单胞菌的生长大都单独采用单一的模型进行预测，对于冷却猪肉来说，不同温度下哪种模型更适用于预测假单胞菌的生长并不清楚。本实验直接以托盘包装的冷却猪肉作为研究对象，假单胞菌出现初始菌值下降趋势的特点；选用不同的模型对数据进行拟合，找出了不同温度下预测假单胞菌生长的最适模型，Baranyi模型是0℃最适的，而5℃和10℃条件下的最适模型分别是修正的Gompertz和Huang模型。因此，通过以上分析和讨论可知，对于复杂的肉品体系而言，不同的温度条件下应该选择最适合的模型而不是单一的模型来预测假单胞菌的生长，这也为冷却猪肉实际生产中建立假单胞菌的预测预报体系提供了理论依据。

3 结 论

低温条件下，托盘包装冷却猪肉中假单胞菌数量在迟滞期出现初始菌值下降的趋势。在0、5、10℃条件下拟合冷却猪肉中假单胞菌生长的最适模型分别是Baranyi、修正的Gompertz和Huang模型。在对冷却猪肉中假单胞菌进行预测时，不同的温度条件下应该选择最适合的模型而不是单一的模型来预测假单胞菌的生长。

[1] 姜英杰, 邹晓葵, 吴菊清. 假单胞菌在猪肉上生长预测模型的建立与验证[J]. 贵州农业科学, 2010, 38(8)： 141-145.

[2] 李苗云. 冷却猪肉中微生物生态分析及货架期预测模型的研究[D]. 南京： 南京农业大学, 2006.

[3] 姜英杰. 假单胞菌和大肠杆菌在冷却猪肉中生长预测模型的建立[D]. 南京： 南京农业大学, 2008.

[4] LIU Fang, YANG Runqing, LI Yunfei. Correlation between growth parameter of spoilage microorganisms and shelf-life of pork stored under air and modified atmosphere at－2, 4 and 10 ℃[J]. Food Microbiology, 2006, 23： 578-583.

[5] LÓPEZ S, PRIETO M, DIJKSTRA J, et al. Statistical evaluation of mathematical models for microbial growth[J]. International Journal of Food Microbiology, 2004, 96： 289-300.

[6] ZWIETERING M H, JONGENBURGER I, ROMBOUTS F M, et al. Modeling of the bacterial growth curve[J]. Applied and Environment Microbiology, 1990, 56： 1875-1881.

[7] BUCHANAN R L, WHITING R C, DAMERT W C. When is simple good enough： a comparison of the Gompertz, Baranyi, and threephase linear models for fitting bacterial growth curves[J]. Food Microbiology, 1997, 14： 313-326.

[8] SCHEPERS A W, THIBAULT J, LACROIX C. Comparison of simple neural networks and nonlinear regression models for descriptive modeling of Lactobacillus helveticus growth in pH-controlled batch cultures[J]. Enzyme and Microbial Technology, 2000, 26： 431-445.

[9] DALGAARD P, KOUTSOUMANIS K. Comparison of maximum specific growth rates and lag times estimated from absorbance and viable count data by different mathematical models[J]. Journal of Microbiology of Methods, 2001, 43： 183-196.

[10] CHEN C Y, NACE G W, IRWIN P L. A 6 × 6 drop plate method for simultaneous colony counting and MPN enumeration of Campylobacter jejuni, Listeria monocytogenes, and Escherichia coli[J]. Journal of Microbiological Methods, 2003, 55： 475-479.

[11] BARANYI J, ROBERTS T A. A dynamic approach to predicting bacterial growth in food[J]. International Journal of Food Microbiology, 1994, 23： 277-294.

[12] BARANYI J, ROBINSON T P, KALOTI A, et al. Predicting growth of Brochothrix thermosphacta at changing temperature[J]. International Journal of Food Microbiology, 1995, 27： 61-75.

[13] HUANG Lihan. Growth kinetics of Listeria monocytogenes in broth and beef frankfurtermal-determination of lag phase duration and exponential growth rate under isothermal conditions[J]. Journal of Food Science, 2008, 73： 235-242.

[14] KILSBY D C, PUGH M E. The relevance of the distribution of microorganisms within batches of food to the control of microbiological hazards from foods[J]. Journal of Application Bacteriology, 1981, 51： 345-354.

[15] LÓPEZ S, PRIETO M, DIJKSTRA J, et al. Statistical evaluation of mathematical models for microbial growth[J]. International Journal of Food Microbiology, 2004, 96： 289-300.

[16] MOTULSKY H J, CHRISSTOPOULOS A. Fitting models to biological data using linear and nonlinear regression[M]. San Diego： A Practical Guide to Curve Fitting, GraphPad Software, 2003.

[17] GILL C O, NEWTON K G. The development of aerobic spoilage flora on meat stored at chill temperature[J]. Journal of Applied Microbiology, 1977, 43： 189-195.

[18] GILL C O, NEWTON K G. The ecology of bacterial spoilage of fresh meat at chill temperature[J]. Meat Science, 1978, 2： 207-217.

[19] YATES G T, SMOTZER T. On the lag phase and initial decline of microbial growth curves[J]. Journal of Theoretical Biology, 2007, 244： 511-517.

[20] BATY F, DELIGENETTE-MULLER M L. Estimating the bacterial lag time： which model, which precision?[J]. International Journal of Food Microbiology, 2004, 91： 261-277.

[21] 杨红菊, 南庆贤. 冷却猪肉主要腐败微生物生长模型的建立[J]. 前沿科技, 2004, 4(3)： 7-10.

[22] 何帆, 徐幸莲, 周光宏. 不同包装条件下冷却猪肉品质特征指标及动态模型研究[J]. 食品科学, 2010, 31(24)： 473-478.

[23] SILVIA A, DONALD W. Development and validation of a mathematical model to describe the growth of Pseudomonas spp. in raw poultry stored under aerobic conditions[J]. International Journal of Food Microbiology, 2007, 120： 287-295.

[24] RADOVAN G, JUDITH K, STEFANIE B, et al. Mathematical modeling for predicting the growth of Pseudomonas spp. in poultry under variable temperature conditions[J]. International Journal of Food Microbiology, 2008, 127： 290-297.

[25] KOUTSOUMANIS K, STAMATION A, SKANDAMIS P, et al. Development of a microbial model for the combined effect of temperature and pH on spoilage of ground meat, and validation of the model under dynamic temperature conditions[J]. Applied and Environmental Microbiology, 2006, 72： 124-134.