改进的动态灰色模型在高铁路基变形预测中的应用＊

张玉芝，杜彦良，孙宝臣

(1.北京交通大学机械与电子控制工程学院，北京 100044;2.石家庄铁道大学河北省大型结构健康诊断与控制重点实验室，河北 石家庄 050043)

高速铁路无砟轨道对轨下基础变形要求严格，路基变形控制标准高，因此，变形监测工作变得异常重要，同时也对变形监测预报的准确性提出了更高的要求［1－2］。从已建成或在建的高铁线下结构的沉降变形可知，沉降变形量级小，停载后，增量更小［1］，因此，相对于小量级的沉降变形，沉降观测数据波动较大，实时预测分析的难度增大，预测精度要求更高。在沉降变形的小样本监测离散数列方面，灰色系统预测模型以其特有的优势得到了很好的应用。其对数据的处理不是求得数据的概率分布和统计规律，而是根据数据的处理方法找出数据间的规律，因而只需较少的数据就可以处理［3］。现有的研究大多在监测完成或持续一段时间之后，运用灰色模型对已有数据对模拟模型进行改进［4－5］。在监测过程中实现实时预测，必须考虑建立动态的灰色预测模型［6－7］。本文首先对灰色预测理论和已有动态预测模型进行分析，对动态灰色预测模型进行了改进，并通过某市市政规划路下穿京沪高铁变形监测项目的部分监测数据验证其改进效果，而后探讨改进的动态灰色预测模型在高铁路基沉降变形预测分析中的适用性。

1 灰色预测模型及已有的动态灰色预测模型

1.1 灰色预测模型的建立及精度

设已知原始参考数据序列为x(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))，x(1)为其1－AGO 序列，z(1)为x(1)的紧邻均值生成序列，也称为背景构造值，其中:

GM(1，1)模型x(0)(k)+a z(1)(k)=b的时间响应序列为［3］

还原值为:

参数a为发展系数，b为灰色作用量，

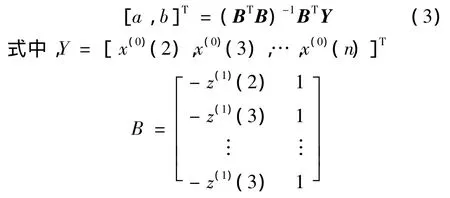
显然:

预测模型模拟精度的检验指标有相对误差，关联度、均方差比值和小误差概率等，在一般情况下，最常用的是相对误差检验指标［3］。相对误差序列为

平均相对误差为:

式中:残差ε(k)=x(0)(k)－(k);k=1，2，…，n。

由于预测模型更需关注预测值的精度，本文中采用相对误差指标和均方差比值c0(a)(残差序列方差与原始序列方差比值)作为预测模型预测精度的检验指标。

1.2 已有的动态灰色预测模型

文献中现有的动态灰色预测模型，为了保证动态灰色预测模型的稳定性和可靠性，基本上都是采用了等维动态序列［6－7］，基本建模步骤如下:

(1)进行1次AGO生成x(1)后建立GM(1，1)模型，得到n+1时刻预测值(n+1);

(2)去掉x(0)(1)，加入实测值x(0)(n+1)，重新构成等维动态序列x1(0)=(x(0)(2)，…，x(0)(n)，x(0)(n+1))，建立新的GM(1，1)模型，预测n+2时刻^x(0)(n+2)，如此递补，逐个预测。

建模后分别进行了3～4步的预测，并通过与静态GM(1，1)模型，以及等维灰数递补模型相比，证明其在短期的动态预测中显示出较高的精度。

已有的研究在选择动态序列后，即建立传统的灰色预测模型GM(1，1)模型，并且基本上都是将动态灰色预测模型用于变化趋于稳定的变形序列［6～7］，进行了少数几步预测。显然，在实际的沉降预测中，变形序列可能会出现波动较大的情况，并且预测分析是需要及时连续进行的，因此，本文从建模机理出发，对数据序列检验、背景构造值和残差等方面分别进行了分析和处理，以提高动态灰色预测模型的精度和稳定性，并通过工程实例的部分数据进行效果验证。

2 改进的动态灰色预测模型建立及实例验证

2.1 改进的动态灰色预测模型建立过程

2.1.1 数据序列检验

首先，为了保证建模方法的可行性，需要对已知数据序列做必要的检验处理，以是否通过级比检验判断选择的序列能否进行灰色预测，计算数列的级比:

使数列y(0)=(y(1)，y(2)，…，y(n))的级比λy(k)落入可容覆盖区内，将其作为新的参考序列。如果经过平移变换，则最终通过其逆运算得到预测值。

2.1.2 基于背景构造值的动态灰色预测模型改进

由模型的建立过程可知，影响模型精度的因素主要有以下几个方面［8］:(1)模型背景值的构造;(2)初值的选取;(3)GM(1，1)模型是一指数模型，它反映的是变形体单纯随时效的变化情况。若有其他外界因素(如荷载的突然变化)对变形或沉降产生较大影响，则会大大影响所建模型的精度［9］;(4)数据列维数的影响。

由于初值函数的构造受人为因素影响较大，因此为提高预测模型的精度，本文改进了背景构造值，建立了动态灰色模型即GM(1，1，a)模型。在GM(1，1，a)模型中，对于 a ∈ (0，1)，背景构造值为:

2.1.3 a 最佳值的判断依据

为充分保证预测值的准确，基于灰色系统理论中的“新信息优先原理”，不同于普通的模拟模型中a最佳值的判断依据［10］，本文中以x(0)n的相对误差Δn(a)为主，平均相对误差¯Δ(a)和均方差比值c0(a)为辅作为a取最佳值的依据，即取Δn(a)绝对值最小时的a为最佳值aopt，且此时¯Δ(a)和c0(a)与两者最小值的取值在同一精度等级内。确定aopt后即可得到改进后的GM(1，1，a)模型预测值(k)。

在实际运算中，若经过上述步骤后发现模拟值仍不满足要求(根据实际情况和监测精度要求取值)，则可以选择aopt和按(3)判据所得的次最佳值a'opt作为GM(1，1，a)模型中a的取值范围，以0.01为取值间隔赋值于a，重复(2)和(3)，直至精度提高不明显为止。

2.1.4 基于残差修正的动态灰色预测模型改进

经过试算，若模拟值的相对误差和残差仍不满足要求，在选择合适维数的实测值序列，满足残差序列修正的条件下，采用残差序列建立GM(1，1)模型，对经背景构造值改进后的模型进行修正，以提高精度。本文中采用累减还原式的残差修正模型。设ε(0)(k0)为建模残差尾段的起始值，由文献［3］可得:

同样，残差修正步骤也可重复进行以提高模型模拟精度。

由以上分析可知:若需得到m个一步预测值，不考虑背景构造值的循环改进和残差修正，仍需建立1个动态灰色模型群。

需要说明的是:无论采取何种改进模型，均是通过尽可能地提高模拟精度来保证预测精度。由于现实工程中冲击扰动的影响以及监测系统误差的存在，即使模拟模型满足精度要求，预测结果与实测值的残差和相对误差不满足精度要求的情况仍然会存在。

2.2 改进模型工程实例验证

某市市政规划路下穿在建的京沪高速铁路，高速铁路无砟轨道铺设已于2个月前完成。桥址处京沪高速铁路预留框架桥已建成，立交桥施工前框架桥已处于填埋状态。新建框架桥采用顶进法施工，工作坑设在京沪铁路北侧，框架桥顶进工作基本完成后，在南侧开始U型槽施工作业。工程位置关系以及测点布设和编号设置如图1所示［11］。

为了及时掌握京沪高速铁路路基的变形情况，采用了基于液力测量的沉降变形自动监测系统为主，精密水准测量的人工监测为辅的监测方式进行监测，保证了数据的连续性和准确性，同时也要求预测模型具有较高的精度和稳定性。

图1 市政规划路工程下穿京沪铁路位置关系及沉降测点布设示意图Fig.1 Sketch map of location relations and measuring points arrangement

本文依托的监测对象在整个监测期间不断受到不同施工工序和外界环境各种因素的干扰，且需要实时进行预测，因此，选择动态灰色预测模型进行预测，建立动态的GM模型群。根据相关规范［12］和精度要求，取模拟精度的相对误差限值为5%，残差限值为0.2 mm。在预测中，基于灰色系统理论中的“新信息优先原理”和“最少信息原理”，通过建模比较精度，时间序列的维数取为5。选取受施工影响较明显的跨中测点部分实测值，观测周期为1 d，分别采用原有的和改进的动态灰色预测模型比较第1步预测(采用第1～5个观测周期的数据预测后期的沉降)和第2步预测((采用第2～6个观测周期的数据预测后期沉降)的结果，如图2所示。

如图2所示，模型计算结果虚线左侧5个观测周期为模拟值，右侧为预测值。模型的模拟精度均较高，尽管如此，由于实测值在第6个观测周期开始，沉降速率明显降低，原有的动态灰色模型预测值残差均较大。改进模型在经过上述改进步骤逐步改进后，新信息得到充分利用，模拟值和预测值残差降低，有助于提高模型预测精度，尤其是一步预测值(即(a)和(b)虚线后的第1个预测值，分别对应第6个和第7个观测周期)，精度较高。

改进的预测模型能否在高速铁路路基沉降长期的实时的预测中表现良好，有待工程实例大量数据的检验分析。

图2 改进模型及已有模型的应用比较Fig.2 Application comparisons of improved and existing models

3 工程实例分析

由以上实例验证可知，在变形数据出现波动时，动态灰色模型短期的预测精度较高，预测步长越远，误差越大。由于第32个观测周期之后，监测暂停，后于第38个观测周期时复测1次，因此，工程实例数据分析中除初始的5个数值和第33～38个观测周期的数值外，保留的均是所采取模型计算所得的一步预测值。据此，建立动态灰色预测模型群。

整个监测过程中，京沪高铁左线和右线上均是跨中测点隆起最大，跨中测点预测值与实测值曲线见图3。预测精度检验如表1所示。

表1 预测精度检验表Table 1 Prediction Precision Test

图3 左线和右线跨中测点14L(R)实测值与预测值时程曲线Fig.3 Measured and predicted values time history curves of both left and right lines middle points14L(R)

距离跨中最远4个测点的预测曲线与实测曲线如图4所示。预测精度检验如表1所示。

由建模过程及以图3～4和表1可得:

(1)改进的动态预测模型在模拟已有监测数据方面虽表现出较高的精度，但由于施工对跨中测点影响较大，对预测值的精度造成的影响相对较大，尽管如此，预测模型在沉降速率变化较大后，由于采用的模型比较充分地利用了新信息，在短时间内预测精度迅速提高，因此，具有一定参考价值。

(2)对于基本不受施工影响的测点，由于其变形量级较小，在沉降速率发生相对较大变化时，预测值存在较大的相对误差，但模型在输入新信息后误差很快减小，残差迅速减小，在整个预测过程中，残差均小于0.2 mm，预测模型表现出较好的适应性。

(3)第32个观测周期之后，监测暂停，后于第38个观测周期时复测1次，预测值与实测值比较吻合。在整个预测过程中，预测模型模拟精度较高，发展系数 －a≤0.3，经综合比较后可以认为，对于受附近施工影响较明显的测点建立的改进动态灰色预测模型比较适应路基沉降的短期实时预测，对于基本不受附近施工影响的测点所建立的模型能够适应路基沉降的中期预测。

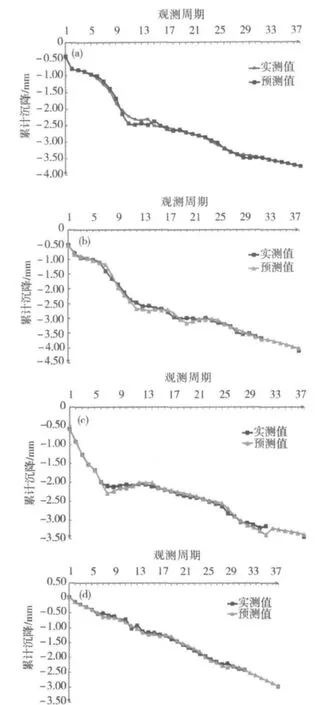
图4 测点1L(R)和24L(R)预测值与实测值时程曲线Fig.4 Measured and predicted values time history curves of 1L(R)and 24L(R)

4 结论及建议

(1)动态灰色预测在高铁路基沉降变形实时预测方面是有一定的优势的。本文建立的改进动态灰色新陈代谢预测模型群，操作简便易行，精度较高，即使对于波动较大的测点，其预测也具有一定的参考价值。本文提出的改进动态灰色预测模型也可用于其他土木工程结构物变形的实时预测预警。

(2)高速铁路线路工程是一个复杂的非线性系统，单纯从变形监测数据挖掘信息量存在不足，并且由于各种预测模型本身不能完全克服的缺陷，因此应结合高速铁路线下工程的结构特征、地质特征和荷载状况等因素，建立系统的数学模型，逐步优化比选，以得到稳定性好、精度高、操作简便的预测方法，进一步促进信息化施工的实现。

［1］陈善雄，宋剑，周全能，等.高速铁路沉降变形观测评估理论与实践［M］.北京:中国铁道出版社，2010.CHEN Shanxiong，SONG Jian，ZHOU Quanneng，et al.Theory and practice of settlement deformation observation and evaluation for high－speed railway［M］.Beijing:China Railway Press，2010.

［2］TB 10621—2009，高速铁路设计规范(试行)［S］.TB 10621—2009，Specifications for plan of high speed railway［S］.

［3］刘思峰，党耀国，方志耕，等.灰色系统理论及其应用［M］.北京:科学出版社，2010.LIU Sifeng，DANG Yaoguo，FANG Zhigeng，et al.Grey system theory and practice［M］.Beijing:Science Press，2010.

［4］杜彦良，姬来，刘新福.高速铁路路基施工期沉降量的灰色预测模型及应用［J］.铁道科学与工程学报.2009，6(1):36－40.DU Yanliang ，JI Lai，L IU Xinfu，Grey prediction model for construction settlement forecast of embankment of high－ speed railway and its application［J］.Journal of Railway Science and Engineering.2009，6(1):36 －40.

［5］刘军勇，薛晖，吴德军.改进灰色模型对路基沉降预测的应用研究［J］.岩土工程技术，2005，15(2):59－62.LIU Junyong，XUE Hui，WU Dejun，Application of improved gray－model in the settlement prediction of roadbed foundation［J］.Geotechnical Engineering Technique，2005，15(2):59 －62.

［6］潘华志，卫建东，夏治国，等.动态灰色模型在变形预测中的应用［J］.测绘科学，2007，32(4):121－123.PAN Huazhi，WEI Jiandong，XIA Zhiguo，et al.Application of dynamic grey model in settlement forecast［J］.Science of Survey and Mapping，2007，32(4):121 －123.

［7］王利，张双成，李亚红.动态灰色预测模型在大坝变形监测及预报中的应用研究［J］.西安科技大学学报，2005，25(3):328 －332.WANG Li，ZHANG Shuangcheng，LI Yahong.Application of dynamic gray forecast model in dam deformation monitoring and forecast［J］.Journal of Xi’an University of Science and Technology，2005，25(3):328 －332.

［8］孙泽信，庞逸群，黄腾.改进的灰色模型在建筑物沉降预测中的应用［J］.测绘工程，2010，19(3):59－62.SUN Zexin，PANG Yiqun，HUANG Teng，Application of improved grey model for forecasting subsidence of the engineering buildings［J］.Engineering of Surveying and Mapping，2010，19(3):59 －62.

［9］DENG Julong.Introduction of grey system［J］.Journal of Grey System，1989(1):1－24.

［10］刘虹，张岐山.基于微粒群算法的GM(1，1，λ)模型的机械产品寿命预测［J］.机械设计，2007，24(10):4 －6.LIU Hong，ZHANG Qishan.Life－ span prediction on mechanical products of GM(1，1，λ)model based on particle swarm algorithm，Journal of Mechanical Design，2007，24(10):4 －6.

［11］张玉芝，杜彦良，孙宝臣，等，基于液力测量的高速铁路无砟轨道路基沉降变形监测方法研究［J］.北京交通大学学报，2013，37(1):36 －41.ZHANG Yuzhi，DU Yanliang，SUN Baochen，et al.Research of high－speed railway ballastless track roadbed settlement monitoring method based on fluid pressure differential［J］.Journal of Beijing Jiaotong University，2013，37(1):36 －41.

［12］客运专线铁路无砟轨道测量技术暂行规范［DB/OL］.http://wenku.baidu.com/view/a7bbc43a5727 a5e9856a61f8.html Measuring Technique Provisional Regulations of Passenger Dedicated Line with ballastless track［DB/OL］.http://wenku.baidu.com/view/a7bbc43a 5727 a5e9856a61f8.html.