任意形状覆盖的数值流形方法初步研究

苏海东，祁勇峰，龚亚琦，颉志强，崔建华

（长江科学院材料与结构研究所，武汉 430010）

任意形状覆盖的数值流形方法初步研究

苏海东，祁勇峰，龚亚琦，颉志强，崔建华

（长江科学院材料与结构研究所，武汉 430010）

在前期研究部分重叠的矩形覆盖基础上，首次提出基于任意形状覆盖的数值流形方法，其特点是：独特的数学覆盖形式，即任意形状的覆盖＋条形的覆盖重叠区域；以独立覆盖为主的分析方式；单位分解函数表述的独特性及严格的插值性。对此方法展开初步研究，给出任意形状覆盖的基本形式，以及基于完全重叠覆盖和自由度之间约束关系的实现方法，算例分析初步验证了该方法的有效性。

数值流形方法；任意形状覆盖；部分重叠覆盖；单位分解

1 研究背景

早在1991年，我国留美学者石根华博士首先将现代数学中的流形思想引入到数值计算中，形成了数值流形方法［1］（以下简称流形法），该方法具有以下特点［1－2］：

（1）数值解的插值区域与实际物理区域分离。流形法引入2套覆盖体系，其一是数学覆盖（又称为数学网格），用于构造物理场的近似解；其二是物理网格，表示材料物理边界，用于定义积分区域。这2套覆盖体系相互独立，只要求前者在空间上完全包容后者，这样，数学网格就不必满足材料边界的要求，数学网格内的材料（被称为“流形元”）可以仅占网格的部分区域。

（2）流形法的2套覆盖体系将求解域划分成有限个相互重叠的集合，称为物理覆盖。在各个覆盖上定义局部覆盖函数，通过权函数联系起来进行加权平均得到整个求解域上的总体场函数。

（3）局部覆盖函数可以有多种选择，如目前最常用的多项式级数，或其它类型的级数甚至是解析解级数。随着级数项数的增加及阶次的提高（即高阶流形法），计算精度得以提高。在局部覆盖函数为多项式级数且权函数也能用多项式表示的情况下，流形法采用单纯形精确积分法，将任意形状的复杂积分区域分解为有向单纯形，分别解析积分后求其有向和。

迄今为止，绝大多数流形法研究采用有限元网格（如矩形或三角形）作为数学网格［3］，与某个有限元结点相连的所有网格构成一个局部数学覆盖，在此覆盖上定义局部覆盖函数，有限单元的形函数作为权函数。以下称这种流形法为常规流形法，其重要特点是：每个有限单元正好就是其几个结点上的数学覆盖的共同区域，或者说，这几个覆盖在有限单元的区域内完全重叠，各覆盖没有自己的独立区域，笔者称之为完全重叠的数学覆盖。研究表明，采用完全重叠覆盖的常规流形法具有以下缺陷：

（1）方程组的线性相关问题。在采用高阶多项式覆盖函数情况下，流形法的线性相关问题［4］表现为线性方程组的解（即多项式系数）存在但不唯一。此问题源于权函数的1阶多项式与局部覆盖函数中1阶基函数的重叠。

（2）网格问题。既然采用了有限元网格，就难以摆脱网格划分的问题，虽然“网格不必满足物理边界”的特性已使流形法的前处理比有限元法方便多了，但为了保证局部区域（如结构分析中的裂纹尖端附近）的计算精度而在所有区域采用细密的均匀网格是不经济的，需考虑局部加密网格，这样就仍然存在大、小网格过渡的问题。

石根华博士指出，目前的流形法只是一个初级版本。从2011年开始，在石根华博士的建议下，笔者开展了新型流形法的研究工作，即部分重叠的矩形覆盖的研究［5－6］。该方法采用以矩形独立覆盖为主的分析方式，独立覆盖之间用较小的条形重叠区域保持覆盖的连续性。与以往的“完全重叠覆盖”相对应，笔者称之为“部分重叠覆盖”。前期研究表明，该方法具有以下优点。

（1）解决了常规流形法的线性相关问题：在覆盖的独立区域内，局部覆盖函数是线性无关的级数，仅在覆盖之间较小的重叠区域存在对覆盖函数的加权，因此，线性相关性即使仍存在也会减弱很多，有利于方程组的快速迭代求解。

（2）适合在局部区域应用解析解：在局部区域的独立覆盖中可以采用特殊的覆盖函数以适应物理场的局部特征，比如在裂尖附近采用特殊的解析解级数，这样就能将数值解法与局部解析法协调起来进行联合求解。

（3）覆盖加密方便：笔者在文献［6］中提出对矩形的独立覆盖进行覆盖加密以提高局部计算精度的简便方法，包括重叠覆盖的加密方式和部分重叠覆盖的加密方式，这种大、小覆盖间的过渡方式是完全协调的。

但上述流形法仍存在本质边界条件施加的问题。由于物理边界与网格不匹配，流形法的本质边界条件一般通过罚函数法施加。这并非是最佳选择，因为罚系数的取值对计算精度和计算稳定性都有一定影响，取值太小会使约束不足，取值太大又会影响方程组性态。另外一个重要问题是，矩形覆盖对于复杂结构而言并不方便，特别是三维问题，比如具有复杂走向的三维裂纹，用规整的长方体去覆盖肯定没有沿着裂纹走向的不规则覆盖更合适。

因此，本文进一步发展部分重叠覆盖的思路，应用基本的数学流形思想，提出基于任意形状覆盖的数值流形方法，简称任意形状覆盖流形法。

2 任意形状覆盖流形法的基本思想

流形［7］是现代数学中的重要课题，其基本思想大致上就是将有限个相对简单的局部拓扑结构用相容的方式黏合成整体上的一个复杂拓扑结构，这种相容方式通常是局部结构之间互相重叠的形式。目前计算力学界所推崇的“单位分解”实际上是流形中的一个重要概念，即：把“1”分解成若干个光滑函数（即单位分解函数）之和，每个光滑函数都在某个局部坐标域（即覆盖）之外恒等于0［7］。如果在每个局部坐标域内都可以用局部坐标表达某个量（相当于采用局部近似函数或局部覆盖函数），那么用单位分解就可以把这些量黏合起来成为定义在整个流形上的量。因此，单位分解是在局部量和整体量之间建立联系的不可缺少的工具。

将单位分解思想应用于数值计算，表述为［8］：采用一些重叠的分片区域Ωi覆盖整个计算域Ω，在每片Ωi上定义局部近似函数Vi，再加上在Ωi上非零的单位分解函数φi，从而构成总体近似函数：

式中：n为覆盖数，φi须满足：

常规流形法中将局部覆盖函数联系起来的权函数实际上就是单位分解函数。

在数学流形中，覆盖形状可具有任意性，覆盖之间一般不是完全重叠的。如图1（a）所示，以平面上3个任意形状的独立覆盖为例，它们只是部分重叠（见图中的白色区域）。然而在这种情况下，单位分解函数很难做到完全的插值性，即：在某个覆盖的独立区域内（图中某一彩色部分），有

且在覆盖的过渡区域（图中的白色区域），φi和φj等单位分解函数满足式（2）。举个反例，如图1中2个覆盖的交点A，φi和φj均等于1。笔者认为，在某种意义上正是由于这个原因，以往的流形法没有采用更灵活多变的数学覆盖，而不得不借用有限元网格的覆盖形式。

针对上述问题，本文提出任意形状覆盖的条形连接方式，如图1（b）所示。在覆盖的条形重叠区域内，满足上述插值性要求的单位分解函数φi很容易用数值方式严格表述（见下文），图中的点A也变成了2个点以便于φi和φj的过渡。

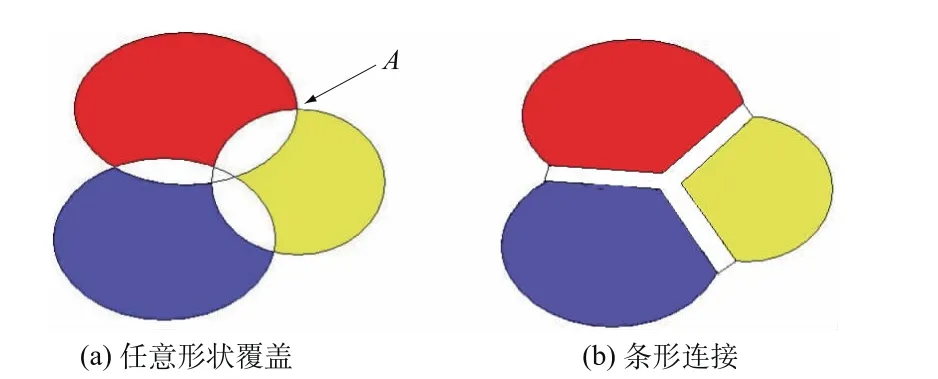
图1 3个任意形状覆盖及其条形连接Fig.1 Three covers of arbitrary shape connected w ith each other through strips

该方法很大程度上反映了现代数学中“流形”的基本思想，笔者认为这才是具有较完整意义的“数值流形方法”。为了与现有的基于有限元网格的常规流形法区分开，本文将其命名为“基于任意形状覆盖的数值流形方法”，简称“任意形状覆盖流形法”，它是部分重叠覆盖思想与任意形状覆盖的组合。

3 任意形状覆盖的实现方法

3.1 单位分解函数的表示

仍以图1所示的3个独立覆盖为例，在覆盖i的独立区域（图中的某个灰度区域）内，此时因为只有1个覆盖（式（2）中的n＝1），则单位分解函数φi＝1。再根据式（1），总体近似函数与局部近似函数相同，即

这样，总体近似函数就表示为独立的覆盖函数，便于采用某种特殊的级数形式（如解析解级数）更好地逼近实际的场函数分布。

在2个覆盖重叠的条形区域，采用有限元网格进行连接，如图2（a）所示的四边形单元，单位分解函数可取为四边形有限单元的形函数，但由于一般四边形的形函数需要采用等参单元的复杂表达式，不能应用单纯形积分公式，因此在实际操作中按图2（b）所示将四边形分割为2个三角形。图2中的3个覆盖的重叠区域正好用一个三角形连接，更多覆盖情况如图3所示，5个覆盖的重叠区域用三角形依次相连。

在上述三角形单元内，单位分解函数为有限单元的形函数，表示为对应于3个结点面积坐标（Li，Lj，Lk），即φi＝Li，φj＝Lj，φk＝Lk，在单元内的任一点满足：

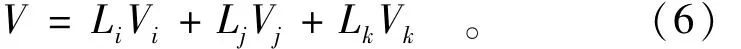
3.2 基于完全重叠覆盖实现任意形状的部分重叠覆盖

任意形状覆盖的流形法具有独特的覆盖形式和单位分解函数的表示方式，本应采用一套新的计算公式及程序，考虑到采用完全重叠覆盖的常规流形法已有一套成熟的公式及程序，本文沿用笔者在文献［5］中提出的方法，基于完全重叠覆盖，用结点自由度之间的强制约束方式来实现任意形状的部分重叠覆盖。

首先，在覆盖的独立区域内形成V＝Vi的独立覆盖函数。以图3为例，在独立区域内取不在同一直线上的3点，如覆盖A中的1，6，7三点，连成三角形的数学网格，令V6＝V7＝V1＝VA（即V6，V7与V1采用同样的自由度），则根据式（6）和式（5）有

即得到式（4）的独立覆盖函数形式。其它独立覆盖同理，如覆盖B，令V8＝V9＝V2＝VB，也可得到V＝VB。

再考虑覆盖A和覆盖B之间的条形重叠区域。在三角形1－7－8中，有V1＝V7＝VA，V8＝VB，则此三角形内任一点的覆盖函数为

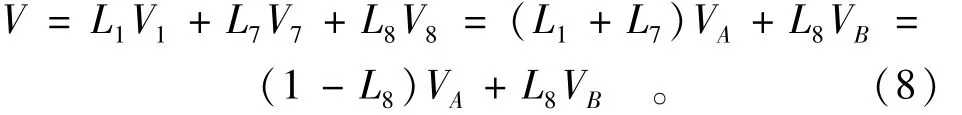
式中1－L8与L8正好满足一维2个覆盖的单位分解函数之和为1的要求（见式（2）），且在边1－7上，V＝VA，在点8处，V＝VB，严格满足插值性要求。在三角形1－8－2中也能得到同样的结论。2个三角形在其公共边1－8上是协调的，形函数的表示式仅与结点1和8相关，该边也满足式（8）以及插值性要求。因此，覆盖A和覆盖B的过渡是协调的。

最后考虑多个覆盖的重叠部位，如覆盖A，B和E的交叉部位——三角形1－2－5，显然，与三角形网格的完全重叠覆盖类似，在该三角形内3个覆盖的单位分解函数满足式（5），且在角点处满足V＝Vi的插值性要求，因此这3个覆盖的过渡也是协调的。三角形2－3－4和三角形2－4－5及其相关覆盖的情况类似。同时可以看出，覆盖A和覆盖C，D之间没有联系，表现在几个覆盖的重叠区内也没有线段将其连接起来。

图2 条形区域内的有限元网格Fig.2 Finite elementmeshes in the strips

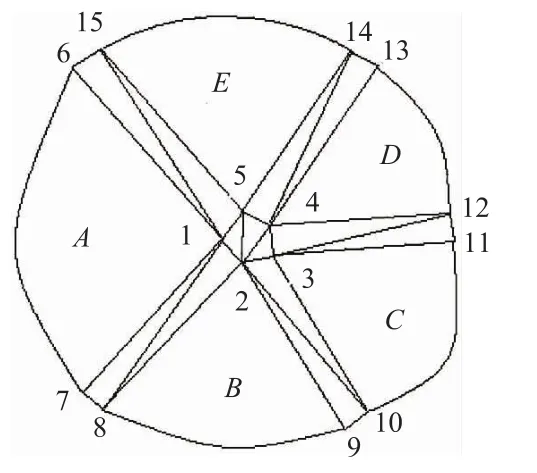
图3 多个任意形状覆盖的连接Fig.3 Connection between several covers of arbitrary shape

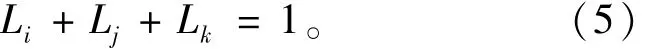
3个结点分别对应于3个局部覆盖函数Vi，Vj，Vk，则总体近似函数为

综上所述，本文提出的独立覆盖之间的条形过渡方式是完全协调的，通过结点之间的强制约束方式，可以很方便地由完全重叠覆盖形式转化为部分重叠覆盖形式。这一方面简化了部分重叠覆盖的生成过程，另一方面还可以将完全重叠覆盖和部分重叠覆盖的程序统一起来，大大简化了程序编写工作，并使程序具有了通用性，从而可以实现完全重叠覆盖和部分重叠覆盖同时存在于一个计算模型中。

本文方法的前处理根据求解域形状布置覆盖：先将求解域分块（可以是任意形状），再块与块之间形成条形连接区域，最终形成任意形状的部分重叠覆盖。需要说明的是，形成块间条形区域是由计算机自动实现的，由于只涉及简单几何运算，因此计算量很小。

4 算例分析

本节通过悬臂梁一端承受集中力的简单结构算例的分析结果说明本文方法的有效性。

如图4所示的悬臂梁，梁长L＝10 m，截面尺寸d＝1 m。在梁的自由端作用有P＝25 kN竖直向下的集中荷载。梁的弹性模量E＝300 MPa，泊松比μ＝0.2。

图4 一端承受集中力荷载的悬臂梁Fig.4 A cantilever beam subjected to a concentrated force in one end

平面应力情况下，位移理论解［9］为

为了形成任意形状的覆盖，本文特意将悬臂梁结构分割成多种形状的块，如图5（a）所示，图中所有多边形块的边数均超过4，因此不能构成通常意义上的平面有限元网格，其中圆形也离散成多边形。图5（b）将分块局部放大，相应地形成图5（c）的条形连接。

在每个独立覆盖内采用2阶或3阶多项式覆盖函数。计算结果显示，梁自由端中点D的垂直向位移计算值为0.335 m，与理论值完全一致。

表1列出了几个典型部位的观测点的应力值，其中点A位于梁的上表面，点B位于中轴线，点C位于圆形覆盖内，见图5（a）。由表1可见，当独立覆盖采用2阶多项式覆盖函数时，各点的应力结果已接近于理论解，如点A处σx的相对误差在1%以下，各点τxy的误差稍大（但其本身的应力数值并不大），而采用3阶多项式覆盖函数时，与理论解的最大相对误差为0.1%左右。

从式（9）可见，该算例的位移理论解是最高为3阶的多项式。在独立覆盖函数为3阶多项式的情况下，分别考虑点A所在的多边形覆盖及点C所在的圆形覆盖，将其位移解的多项式函数表达式扩展到整个悬臂梁，与式（9）的理论解进行对比，取悬臂梁的中轴线绘制垂直向位移分布，如图6所示。从图中可见，位移计算值与理论值的2条曲线几乎完全重合。这表明在此悬臂梁算例中，各独立覆盖采用3阶多项式覆盖函数就可以达到精确解，可以用某个局部独立覆盖的多项式位移解代替整个梁的位移解。

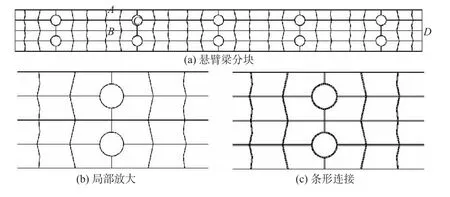
图5 悬臂梁分块及条形连接Fig.5 The cantilever beam divided into blocks connected through strips

图6 悬臂梁轴线y向位移Fig.6 Vertical displacements in the beam axis

上述结果表明，本文方法只要采用了足够的多项式阶次就能够很好地逼近真实解。

表1 各观测点的应力Table 1 Stresses at som emeasurem ent points

5 结 语

与采用有限元网格的常规流形法不同，本文方法具有以下重要特点。

（1）覆盖形式的独特性：任意形状覆盖＋条形重叠区域。数学覆盖与物理区域整体重合，再没有常规流形法在数学网格中可能存在的空白数学覆盖区域（事实上，求解域以外的覆盖区域无意义），覆盖本身既作为插值区域又作为积分区域，其中，对于多项式函数仍可采用单纯形积分。与有限元网格需要保持单元结点的正确连接以及合理的单元形状不同，这种任意形状的覆盖可适应任何复杂边界，从而使前处理的难度大大降低。当然，代价是要形成覆盖之间的条形连接，需要再次强调的是，这只涉及简单几何运算，不仅计算量很小而且可由计算机自动完成。

（2）单位分解函数表述的独特性：在覆盖的独立区域内φi＝1，在条形重叠区域内采用数值方式定义φi，满足单位分解函数合成为1的要求，并具有严格的插值性。

（3）以独立覆盖为主的分析方式：重点研究相对较大的独立区域内的覆盖函数Vi。本方法属于部分重叠覆盖方法，能够解决高阶流形法的线性相关问题，并容易实现覆盖加密。

事实上，这种新的覆盖体系引入了一种新的物理场逼近方式，因此，该方法的应用不仅适用于文中算例所涉及的结构分析领域，也适用于研究其它物理场。当然，该方法目前还处于起步阶段，还有很多基础理论问题（如逼近特性）需要研究。进一步的研究发现：与有限元法、单位分解（有限元）法、无网格等方法相比，任意形状覆盖流形法具有自身的特点和优势，如以独立覆盖为主的分析方式便于在局部区域采用特殊覆盖函数（如解析解）以适合物理场局部特征，能够准确施加本质边界条件，覆盖加密方便，具有多方面的兼容性和程序实现的方便性等，这些成果将另文介绍。

致谢：在此衷心感谢石根华博士对本文的指导！

［1］ SHIG H.Manifold Method of Material Analysis［C］∥Proceedings of the Ninth Army Conference on Applied Mathematics and Computing.Minneapolis，Minnesota，U.S.A.，June 18－21，1991：51－76.

［2］ 石根华.数值流形方法与非连续变形分析［M］.裴觉民译.北京：清华大学出版社，1997.（SHIGen hua.Numerical Manifold Method（NMM）and Discontinuous Deformation Analysis（DDA）［M］.Translated by PEI Jue min.Beijing：Tsinghua University Press，1997.（in Chinese））

［3］ 张湘伟，章争荣，吕文阁，等.数值流形方法研究及应用进展［J］.力学进展，2010，40（1）：1－12.（ZHANG Xiang wei，ZHANG Zheng rong，LV Wen ge，et al.Ad vances and Perspectives in Numerical Manifold Method and Its Applications［J］.Advances in Mechanics，2010，40（1）：1－12.（in Chinese））

［4］ TERADA K，ASAI M，YAMAGISHI M.Finite Cover Method for Linear and Nonlinear Analysis of Heterogene ous Solids［J］.International Journal for Numerical Meth ods in Engineering，2003，58（9）：1321－1346.

［5］ 祁勇峰，苏海东，崔建华.部分重叠覆盖的数值流形方法初步研究［J］.长江科学院院报，2013，30（1）：65－70.（QIYong feng，SU Hai dong，CUIJian hua.Prelimi nary Study of NumericalManifold Method with Partially O verlapping Covers［J］.Journal of Yangtze River Scientific Research Institute，2013，30（1）：65－70.（in Chinese））

［6］ 苏海东，祁勇峰.部分重叠覆盖流形法的覆盖加密方法［J］.长江科学院院报，2013，30（7）：95－100.（SU Hai dong，QI Yong feng.Cover Refinement Method in Numerical Manifold Method with Partially Overlapping Covers［J］.Journal of Yangtze River Scientific Research Institute，2013，30（7）：95－100.（in Chinese））

［7］ 陈维桓.流形上的微积分（2版）［M］.北京：高等教育出版社，2003.（CHENWei huan.Calculus on Manifolds（Second Edition）［M］.Beijing：Higher Education Press，2003.（in Chinese））

［8］ BABUSKA I，MELENK JM.The Partition of Unity Meth od［J］.International Journal for Numerical Methods in Engineering，1997，40（4）：727－758.

［9］ 钱伟长，叶开沅.弹性力学［M］.北京：科学出版社，1956：213－242.（QIANWei chang，YE Kai yuan.Elas ticity［M］.Beijing：Science Press，1956：213－242.（in Chinese） ）

（编辑：黄 玲）

Prelim inary Research of Numerical M anifold M ethod Based on Covers of Arbitrary Shape

SU Hai dong，QIYong feng，GONG Ya qi，XIE Zhi qiang，CUIJian hua
（Department of Material and Engineering Structure，Yangtze River Scientific Research Institute，Wuhan 430010，China）

Numerical Manifold Method（NMM）with covers of arbitrary shape is presented for the first time based onprevious research of partially overlapping rectangular covers.The characteristics of thismethod are as follows：cov erswith arbitrary shape are connected with each other through strips；it has a unique analysismodemainly invol ving independent covers；the functions of the Partition of Unity（PU）are presented in a special way with strict in terpolation properties.The fundamental forms of covers of arbitrary shape，aswell as the realization method based on totally overlapping covers by using freedom constraint are given.Finally，the validity of the new method is dem onstrated by a numerical example.

Numerical Manifold Method（NMM）；covers of arbitrary shape；partially overlapping covers；Partition of Unity（PU）

TB115；TV311

A

1001－5485（2013）12－0091－06

10.3969／j.issn.1001－5485.2013.12.017

2013－07－04；

2013－09－04

中央级公益性科研院所基本科研业务费项目（CKSF2013031，CKSF0210012）

苏海东（1968－），男，湖北武汉人，教授级高级工程师，博士，主要从事水工结构数值分析工作和计算方法研究，（电话）027－82829754（电子信箱）suhd＠mail.crsri.cn。