整数型铁路线路养护维修计划优化模型

郭 然,韩宝明,王福田

(北京交通大学交通运输学院,北京100044)

整数型铁路线路养护维修计划优化模型

郭 然,韩宝明*,王福田

(北京交通大学交通运输学院,北京100044)

制定铁路线路养护维修计划既要保证线路充分维修,又要兼顾经济效益.为此,以区域路网为研究对象,建立了基于整数规划的铁路线路养护维修计划优化模型.模型考虑了路网中线路之间维修资源的约束,以维修时间和股道占用状态为决策变量,以股道占用费用、维修费用及惩罚费用总和最小化为目标,通过集中安排线路中各项养护维修活动节省维修支出,减少维修活动对股道的占用时间进而达到优化目的.基于启发式算法设计了模型求解方法,仿真实验结果表明,模型具有较好的实用性,能够为编制铁路线路年度养护维修计划提供决策支持.

铁路运输;养护维修计划;整数规划;优化模型;启发式算法

1 引 言

铁路线路作为机车车辆和列车运行的基础,是列车安全、平稳和不间断运行的重要保障.随着铁路向高速、重载方向发展,列车运行速度和密度越来越高,线路设备养护维修工作量不断增加,维修费用逐年上升[1].如何在充分做好线路设备养护维修工作的同时,寻求与维修资金投入之间的最佳平衡是各国铁路部门面临的重要课题.制定高效、合理的铁路线路养护维修计划,对于确保铁路线路高可靠性,保障正常运输组织秩序,节省维修费用,合理配置维修资源具有非常重要的意义.

铁路基础设施的养护维修计划编制问题一直备受关注,目前,国内外学者的研究方法主要有两类:以设备状态为中心的维修计划编制方法(Conditional Maintenance,CM)和以设备可靠性为中心的维修计划编制方法(Reliability Centered Maintenance,RCM).第一类方法以设备状态监测数据为支撑,通过建立劣化模型预测设备状态变化情况并安排维修[2-5],但该方法主要应用于铁路轨道养护维修计划编制,且需要积累大量的轨道状态检测数据以预测轨道状态变化;第二类方法通过建立设备寿命分布模型,以维修费用或设备可靠度为优化目标来安排维修,在铁路接触网悬挂系统和牵引供电系统维修计划编制领域有广泛应用[6-9],并设计了基于RCM的铁路基础设施维修管理系统[10].但对于铁路线路设备养护维修计划,RCM通常以特定设备类型为研究对象,只能制定单一养护维修活动(如轨枕更换)的实施计划[11-13].铁路线路是包含多种设备的复杂系统,难以全面掌握各类设备的状态监测数据,同时,线路养护维修活动类型多,各项活动相互影响,上述两类计划编制方法尚未直接应用于制定铁路线路养护维修计划.

针对上述问题,荷兰学者Budai提出了一种铁路线路预防性养护维修计划编制模型(Preventive Maintenance Scheduling Model,PMSM),在已知线路预防性养护维修活动及其周期的前提下,尽可能集中安排各项活动,以减少股道占用时间,并降低维修费用[14].但PMSM仅针对具体的一条铁路线路,无法编制包含多条线路的路网线路养护维修计划.

因此,本文基于PMSM,提出了区域路网铁路线路养护维修计划编制模型并设计了求解算法.文中首先根据铁路线路养护维修活动的特点和模型的适用条件进行了相关的定义及假设;然后,考虑了路网内多条铁路线路之间维修资源分配的约束,以养护维修时间与股道占用情况为决策变量,以股道占用费用、维修费用及惩罚费用总和最小化为目标,构建了基于整数规划的区域路网线路年度养护维修计划优化模型;最后,设计了模型求解的启发式算法并进行了仿真研究.

2 相关定义及假设

综合文献[15,16],进行如下定义:

定义一 围绕线路设备养护维修工作所进行的各种活动统称为修理活动,并划分修理活动为维修活动和施工活动.

定义二 维修活动指股道占用时间短、执行频繁的周期性修理活动,主要包括线路设备周期性人工外观检查、仪器检测,以及定期整修和更换失效零部件等[16].对于设备发生故障或病害后采取的事后维修(又称为纠错性维修)不属于本文定义的维修活动范畴.

维修活动的执行周期从每月几次到几个月一次不等,且由于运营繁忙程度的差异,同一项维修活动在干线铁路执行频率高于非干线铁路.

定义三 施工活动指持续时间长、作业量大、影响范围广的修理活动,如:线路全面捣固、成段更换钢轨、成组更换道岔和轨枕等[16].

施工活动需借助大型养路机械,并根据通过总重及钢轨累计疲劳伤损率确定线路施工时间,一般2～3年安排一次[15].

模型假设如下:

(1)区域路网中每条线路需安排的维修活动与施工活动已确定,模型只考虑如何在年度计划中安排已知修理活动使总费用最小;

(2)所有维修活动在计划时间范围内按照固定周期执行;

(3)线路运营过程中的纠错性维修,不会影响计划中维修活动和施工活动的安排.

3 模型构建

3.1 模型框架

区域路网线路养护维修计划优化模型(OptimizingModelofMaintenancePlanningfor Regional Railway Network,OMMP-RRN)框架如图1所示.

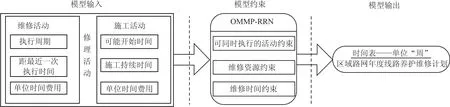
图1 模型整体架构图Fig.1 Diagram of model structure

模型输入条件包括:路网中各线路的维修活动集合,及各项维修活动的执行周期、距离最近一次维修的时间、单位时间维修费用;路网中各线路的施工活动集合,及各项施工活动可能开始时间、持续时间、单位时间施工费用.模型约束包括可同时安排执行的活动约束,该约束使活动尽可能的集中执行,最大程度节省股道占用时间,提高资源利用率,此外,模型还考虑了区域路网的维修资源约束及年度中无法进行施工的时间约束.模型的输出结果为以“周”为时间单位的区域路网年度线路养护维修计划时间表.

3.2 模型符号说明

文中以RN=(SN,RL)表示区域路网,SN= {s1,s2,…,smax}与RL={l1,l2,…,lmax}分别表示RN中关键节点和线路的集合.RN的年度线路养护维修计划日期范围用H表示,T为该范围内以“周”为单位的时间集合.模型中其他的参数定义如下:

PAl——线路l的施工活动集合,l∈RL;

RAl——线路l的维修活动集合,l∈RL;

Al——PAl∪RAl,线路l的所有修理活动集合,l∈RL;

Cl——可合并(即可在单位时间内同时安排执行)的修理活动集合,{(m,n)|修理活动m可与n合并,∀m,n∈Al};

Lal——线路l维修活动a的执行周期,l∈RL,a∈RAl;

Gal——线路l维修活动a最近一次执行完成后到计划开始日期所经历的时间,l∈RL,a∈RAl;

LCal——{t∈T|1+H-Lal≤t≤H}⊆T,计划范围内线路l维修活动a最后一个周期内的时间集合,l∈RL,a∈RAl;

从时间t到计划结束的剩余时间与线路l的维修活动a执行周期的比,t∈

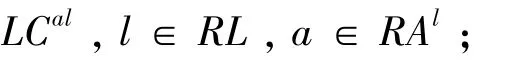
线路l的施工活动p可能开执行的时间集合,l∈RL,p∈PAl;

Tn——Tn⊂T,年度养护维修计划日期范围内禁止线路进行施工的时间集合;——线路l的施工活动p持续实施时间,l∈RL,p∈PAl;

模型中的决策变量定义如下:

3.3 目标函数及约束

区域路网线路养护维修计划优化模型(OMMP-RRN)如下:

模型约束中,式(2)为当前计划中维修活动首次执行时间约束,表示在计划开始后,每一项维修活动首次安排执行的时间范围;式(3)约束了路网中每项维修活动都按固定周期执行;式(4)表示各线路中不能合并的修理项目禁止在同一单位时间安排执行;式(5)、式(6)表示路网中每一项施工活动在时间范围H内只安排一次,且当施工活动开始后,其持续实施的时间长度为Dpl;式(7)为路网中禁止施工的时间约束,由于大型养路机械作业轨温限制及对正常运输的较大干扰,夏季(7～8月)、冬季(11～1月)禁止施工[3];考虑到可作业的大型养路机械资源有限,式(8)约束了路网中可同时进行的施工活动数量的上限;式(9)表示t时刻,若线路股道由于进行修理活动被占用,则该线路上至少安排了一项修理活动;式(10)表示模型中决策变量均为0-1整数型变量.

4 启发式求解算法

本文基于MFWF(Most Frequent Work First Heuristic)方法[14]提出了求解OMMP-RRN模型的启发式算法,算法设计遵循以下原则:

(1)考虑到线路间维修活动的执行互不影响,首先,分别安排各线路的维修活动,使每条线路的维修活动尽可能集中.对于任意一条线路,按照周期递增的顺序排列各项维修活动并依次进行安排.

(2)确定各线路维修活动执行时间后,根据施工活动的最早可能开始时间,递增排列路网中所有施工活动并依次安排,使每一项施工活动与同线路中已安排的维修活动在时间上尽量集中,且路网所有线路内同时进行的施工活动数量不能超过所规定的上限.

算法流程如图2所示,具体步骤如表1所示.

图2 模型启发式算法流程图Fig.2 Flow chart of heuristic algorithm for the model

表1 模型启发式算法详细步骤Table 1 The detailed steps of heuristic algorithm for the model

5 案例研究

5.1 案例描述

本节设计了区域路网用于案例研究,应用OMMP-RRN模型编制以“周”为基本时间单位的路网年度(H=52)养护维修计划.设计路网中包含6条铁路线路,假设线路l1、l2、l3、l4为路网中主要干线,l5、l6为非干线.假设计划中需安排执行的活动包括10种不同类型的维修活动Ri与5种施工活动Pj,线路与修理活动的对应关系如表2所示.符号表示在年度养护维修计划中当前线路需安排该种类型的修理活动.

表2 设计路网线路修理活动列表Table 2 List of maintenance activities in designed railway network

根据模型中的约束,设置下列求解条件:路网中的每一条线路上,单位时间内任意两项施工活动不能同时执行,其余活动都可在单位时间内同时执行;整个路网中允许至多3项施工活动同时进行,即Qtmax=3.

模型中的其余参数取值如下:各项修理活动的费用取1～100间的均匀随机数mca～U[1,100];考虑到同一类维修活动的周期会依据线路在路网中的重要程度有所不同,文中干线(l1、l2、l3、l4)上各项维修活动的周期取2～26之间的均匀随机数La～U[2,26],非干线(l5、l6)上对应维修活动的周期略长,为La+3;各项维修活动距离最近一次执行的时间取0～La之间的均匀随机数Ga～U[0,La];各项施工活动最早可能开始时间取1～52之间的均匀随机数ESp～U[1,52],最晚可能开始时间取ESp～(52-ESp)之间的均匀随机数LSp～U[ESp,52-ESp],施工持续时间取1～4之间的均匀随机数Dp～U[1,4],年度计划中禁止进行施工的时间段为[1,12]∪[26,32];路网中干线每单位时间的股道占用费用为pcli=75,li∈{l1、l2、l3、l4},非干线每单位时间的股道占用费用为pclj=25,lj∈{l5,l6}.

5.2 模型求解结果

根据5.1节中的参数取值,利用启发式算法求解模型,模型求解的硬件环境为:Intel(R)Core (TM)2 CUP,主频1.83 GHz,内存2.00 GB, Windows Server 32位操作系统.求解耗时1分27秒,最优年度线路养护维修计划的费用目标函数值为25 670.7,模型求解结果以图3的形式展示.图中垂直方向为路网中每条线路需要安排的修理活动,水平方向为以“周”为单位的计划时间,灰色实心方框代表活动将在对应的时间安排执行.由仿真结果可以看出:各条线路的修理活动都普遍集中,其中,线路l1和l2在同一周内同时安排3项及以上修理活动的周次分别占总计划时间(H=52)的17.3%和25.0%;这样,线路中未安排维修计划的周次得到最大程度的增加,如线路l5和l6中未安排维修的周次分别占总计划时间(H=52)的65.4%和67.3%.上述编制结果使线路得到充分养护维修的同时,减少了由于养护维修造成的股道占用,增加了股道空闲时间,降低了修理的总成本.

图3 区域路网年度线路养护维修计划时间表Fig.3 Annual maintenance planning timetable for regional railway network

6 研究结论

合理安排线路设备养护维修既能够保持线路设备完整和质量均衡、延长设备使用寿命,还能最大程度地减少运营支出,提高维修工作效率.因此,为制定最优化的线路养护维修计划,本文以区域路网下的多条铁路线路为研究对象,以费用最小化为目标提出了基于整数规划的养护维修计划优化模型,主要工作成果总结如下:

(1)模型目标函数考虑了三部分的费用:维修费用、股道占用费用和惩罚费用,通过在单位时间内集中安排维修活动和施工活动,有效减少股道占用时间,优化了目标函数,同时,惩罚费用的设置使模型能够适用于连续的计划编制.

(2)模型考虑了路网中维修资源有限,结合现场实际情况,设置了避免多项施工活动集中进行的约束条件及禁止施工的时间范围,证明合理有效.

(3)根据维修活动按周期执行的特点设计了启发式算法并求解模型,并通过仿真实验生成了区域路网中各线路以“周”为时间单位的年度养护维修计划.仿真结果表明,该模型计算效率较高,可操作性强,具有较大的实用价值.

本文模型未考虑列车运行计划与线路养护维修计划编制之间的相互影响,在下一步研究中将融入列车运行计划中的相关约束,进一步完善模型.

[1] Higgins A.Scheduling of railway maintenance activities and crews[J].Journal of the Operational Research Society,1998,49:1026-1033.

[2] 许玉德,曾学贵.建立整数型轨道状态最优综合维修计划模型[J].铁道学报,2003,25(6):85-88.[XU Y D,ZENG X G.Foundation of the optimized comprehensive integral track maintenance plan model [J].Journal of the China Railway Society,2003,25 (6):85-88.]

[3] 周宇,许玉德.基于遗传算法的轨道状态最优综合维修计划模型改进[J].华东交通大学学报,2005, 22(1):15-20.[ZHOU Y,XU Y D.Designing of optimization track synthetical maintenance plan model based on genetic algorithms[J].Journal of East ChinaJiaotong University,2005,22(1):15-20.]

[4] Vale C,Ribeiro I,Calçada R.Integerprogramming to optimize tampinginrailwaytracksaspreventive maintenance[J].Journal of Transportation Engineering, 2012,137(1):123-131.

[5] Miwa M.Mathematicalprogramming model analysis for the optimal track maintenance schedule[R].Japan: Railway Technical Research Institute,2002,43(3): 131-136.

[6] 李雪,吴俊勇,杨媛,等.高速铁路接触网悬挂系统维修计划的优化研究[J].铁道学报,2010,32(2): 24-29.[LI X,WU J Y,YANG Y,et al.Research on optimization of catenary system maintenance schedule for high-speed railways[J].Journal of the China Railway Society,2010,32(2):24-29.]

[7] 陈绍宽,彭宏勤,毛保华,等.基于费用最小的铁路牵引变电所维修计划优化模型[J].铁道学报, 2011,32(8):39-44.[CHEN S K,PENG H Q,MAO B H,et al.Optimization model of least-cost-based maintenance schedules for railway traction substations [J].Journal of the China Railway Society,2011,32 (8):39-44.]

[8] 陈绍宽,贾顺平,杜鹏,等.基于可靠性最大的铁路牵引变电所维修计划优化模型[J].交通运输系统工程与信息,2011,11(3):43-49.[CHEN S K,JIA S P,DU P,et al.Highest reliability-based optimum maintenance scheduling model for traction substations in railways[J].Journal of Transportation Systems Engineering and Information Technology,2011,11 (3):43-49.]

[9] 陈民武,李群湛,解绍锋.牵引供电系统维修计划的优化与仿真[J].华南理工大学学报(自然科学版), 2009,37(11):100-106.[CHEN M W,LI Q Z,XIE S F.Optimization and simulation of maintenance plan of traction power supply systems[J].Journal of South China UniversityofTechnology(NaturalScience Edition),2009,37(11):100-106.]

[10] 余泽西.基于RCM的铁路基础设施维修管理信息系统的设计[J].交通运输系统工程与信息,2009,9 (2):161-164.[YU Z X.RCM based design for comprehensive maintenance management information system ofrailwayinfrastructure[J].Journalof Transportation Systems Engineering and Information Technology,2009,9(2):161-164.]

[11] Zhao J,Chan AHC,Burrow MPN.Reliabilityanalysis and maintenance decision for railway sleepers using track conditioninformation[J].Journalofthe Operational Research Society,2007,58:1047-1055.

[12] Zhao J,Chan AHC,Burrow MPN.Ageneticalgorithm-based approach for scheduling the renewal of railway track components[J].Proceedings of the Institution of Mechanical Engineers Part F-Journal of Rail and Rapid Transit,2009,223:533-541.

[13] Zhang T,Andrews J,Wang R.Optimal scheduling of track maintenance on a railway network[J].Quality and Reliability Engineering International,2012.

[14] Budai G,Huisman D,Dekker R.Schedulingpreventive railway maintenance activities[J].Journal of the OperationalResearchSociety,2006,57(9): 1035-1044.

[15] Coenraad Esveld.Model railway track(the second edition)[M].MRT-Productions:Zaltbommel,2001: 350-400.

[16] 中华人民共和国铁道部.铁路线路修理规则[S].北京:中国铁道出版社,2010.[The Ministry of Railways of The People's Republic of China.Repair rules for railwaylines[S].Beijing:ChinaRailway Press,2010.]

Integral Optimization Model for Scheduling Railway Maintenance

GUO Ran,HAN Bao-ming,WANG Fu-tian
(School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China)

Scheduling railway maintenance should guarantee both sufficient maintenance and economic benefit.Therefore,taking regional railway network as research object,this paper develops an optimization model of railway maintenance plan based on integer programming.Considering the constraint of maintenance resources for lines in a regional railway network,the maintenance time and the condition of track possession are used as decision variables,and the minimum total cost of track possession,maintenance and penalty are used as target function in this model.The track possession time is reduced,and the optimal objective achieved finally with scheduling all the maintenance activities clustered.The simulated results based on the heuristic algorithm indicate that the proposed model is strong adaptability and can provide decision support for scheduling annual railway maintenance in a network.

railway transportation;maintenance plan;integer programming;optimization model; heuristic algorithm

U216.2Document code: A

U216.2

A

1009-6744(2013)04-0149-08

2013-01-29

2013-03-15录用日期:2013-03-25

国家科技支撑计划(2009BAG12A10).

郭然(1984-),男,山东济宁人,博士生.

*通讯作者:bmhan@bjtu.edu.cn