行星牵引传动的行星轮弹性设计与分析
舒 幻,刘禹智
(1.重庆耐得工业股份有限公司,重庆 401120;2.重庆市农业委员会,重庆 401121)
行星牵引传动机构因其在振动、噪声方面的优势,在很多场合取代了传统的行星齿轮传动机构,得到了越来越多的应用[1]。为保证传动过程中太阳轮与行星轮、行星轮与外圈之间有足够的牵引力,要求初始装配条件下行星轮与太阳轮、外圈之间有很大的压紧力[2]。行星牵引传动机构的传动副之间如何加载合适的压紧力是牵引传动设计的关键,也是一大难点[3-4]。
此前许多国内外学者对牵引传动压紧力做了大量的研究。周建军[5]提出带有锥度薄壁环的加压机构,但没有对此结构做进一步的计算分析,可行性有待验证。宣海军和吴荣仁[6]提出了一种液压控制的弹性圈机构,但其结构较复杂,成本较高,不适合用于小型的牵引传动中。其他学者针对牵引传动的压紧力问题,也提出了许多不同看法,但大多没有经过严密的计算与验证,实用价值不高。
本文行星牵引传动机构的行星轮采用了中空结构,通过行星轮自身的弯曲变形来提供传动副之间的压紧力。通过预先的计算,设置行星轮的弯曲变形量获得合适的压紧力,并预留出合理的磨损量以保证其使用的稳定性。本文运用ANSYS Workbench有限元分析软件分析了行星轮的应力与径向变形情况,又用动态分析验证了设计方案的可行性,最终得出设计结果,为弹性行星轮的设计与分析提供了一种合理、可靠的方法。
1 理论分析
1.1 结构及工作原理介绍
行星牵引传动减速器的结构如图1所示,太阳轮为输入轴,与电机转子相连接,外圈为输出结构,中间3个行星轮起传递力矩的作用。中空弹性行星轮如图2所示,不同于传统的行星轮,其结构为中空结构,弹性行星轮自由形态下的直径略大于其装配尺寸。装配之后由于受到来自太阳轮和外圈的径向压力,弹性行星轮被压成一个椭圆形。通过对中空行星轮的变形分析,预先计算好行星轮径向变形量,就可以准确获得相应的压紧力,而且中空行星轮的弯曲变形使得它与外圈、中心轮的接触面积增大,接触应力减小,有利于提高牵引副的接触寿命[7]。此外,考虑到行星轮产生磨损后造成传动机构压紧力减小的问题,可以为行星轮预留一定的磨损量,增加行星牵引机构的使用寿命。
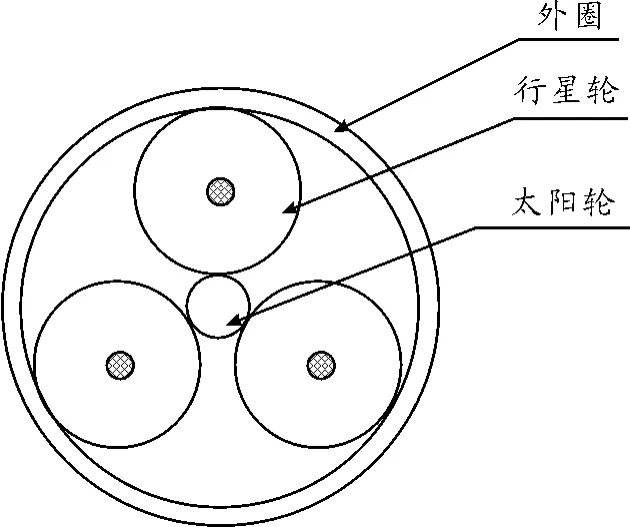
图1 行星牵引传动减速器结构
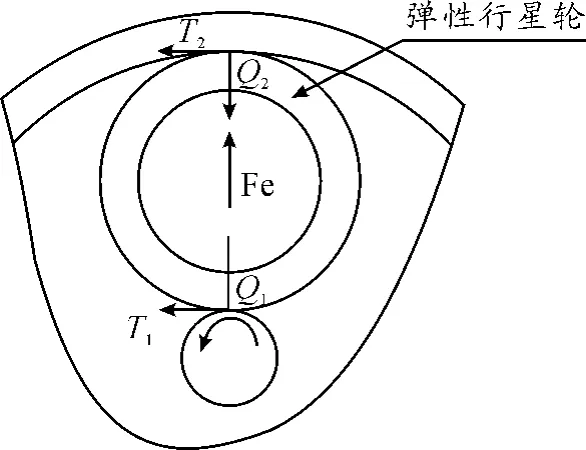
图2 中空弹性行星轮结构
1.2 最小压紧力计算
图2为行星轮的受力情况,行星轮运转时,主要受到太阳轮对其的正压力Q1、牵引力T1、外圈对其正压力Q2、牵引力T2、向心力Fe。静止状态下,压紧力Q1=Q2,运转状态下,Q1+Fe=Q2。由于向心力非常小,计算时忽略不计[8]。
最小压紧力Q为2个互相压紧的牵引轮在不打滑条件下以稳定的传动比传递功率或运动,以产生足够大的牵引力克服从动轮的阻力矩所需要的最小压紧力。克服从动轮阻力矩所需的最小圆周力T称为传递的名义载荷。对于圆柱牵引轮,最小压紧力计算公式为[9]
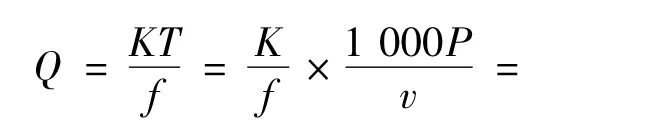
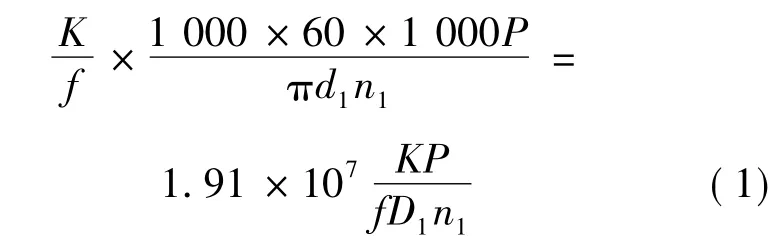
式中:K为载荷系数;P为传动功率(kW);f为牵引系数;D1为主动轮直径(mm);n1为主动轮转速(r/min)。
电机总功率是180 W,每个行星轮传递的功率P1=60 W。通过查阅机械设计手册可知[9],目前牵引油的牵引系数最高为0.09~0.12,本文选取0.10。D1为太阳轮直径,D1=8 mm,太阳轮转速n1=1 520 r/min。行星轮的装配尺寸为D=34 mm,高度L=10 mm。考虑到电机车工作中冲击较大,选载荷系数K=5。将上述数值代入公式,可以求得行星轮传递额定功率所需的最小压紧力
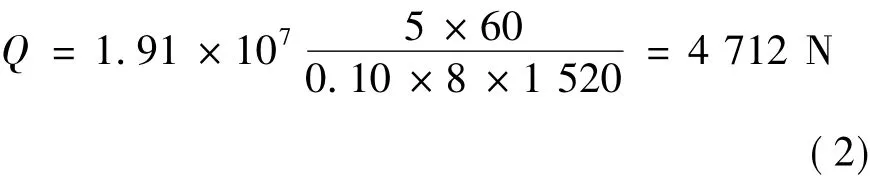
由式(2)计算得,只有行星牵引减速器牵引副之间的正压力最小为4 712 N才能保证其正常工作。
1.3 中空弹性行星轮的变形和应力分析
中空弹性行星轮主要是通过自身的弯曲变形来提供压紧力,通过对中空行星轮的变形分析,预先计算好行星轮尺寸变形量,就可以准确获得所需的压紧力[11-12]。
把中空滚子简化为压紧力轴向分布均匀的对径受压圆环,因圆环结构和受力均是对称的,故考虑以1/4圆环建立原点沿中径rm圆周移动的XY坐标系[13],如图3所示。设作用于圆环截面的垂直力在拉伸时为正,弯矩在使圆环曲率减小时为正,由对称性断定,截面m0n0上的剪力V=0,垂直力N=-Q/2,设m0n0面上的弯矩M=M0,则任意横截面有:
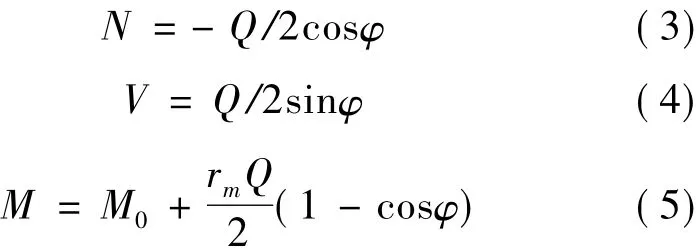
因m0n0面不发生转动,由卡氏定理得
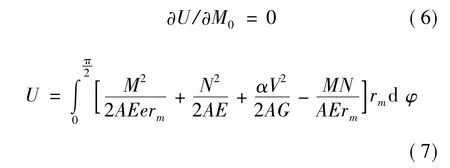
式中的圆环结构参数 A、m、α、e参见文献[14],解得:
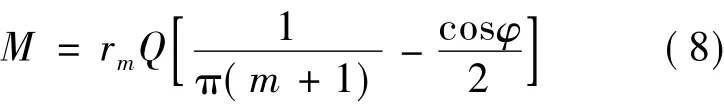
由曲杆应力表示式求得在压紧力作用点下方表面的最大应力
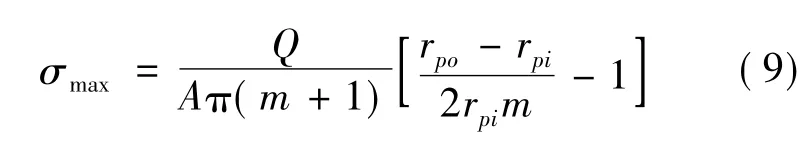
圆环直径在压紧力方向的径向减小量
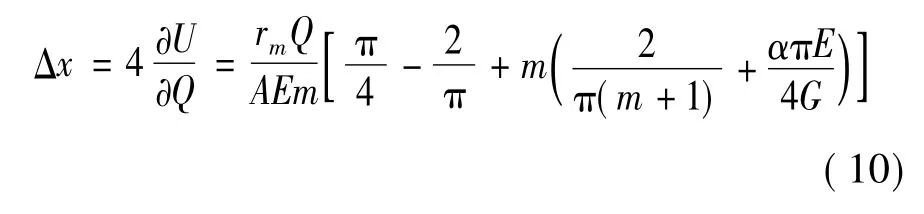
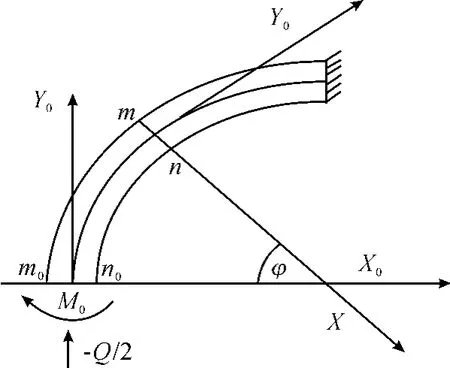
图3 中空弹性行星轮受力分析
2 径向变形和应力分析
利用ANSYS Workbench有限元分析软件,计算不同壁厚的中空弹性行星轮的变形和应力。在ANSYS Workbench中建立装配体模型,并划分网格,如图4所示。行星轮的材料选择一般常用的GCr15,高铬轴承钢GCr15实验材料的传统疲劳极限约为1 185 MPa[15]。对所建模型加载4 712 N正压力,并计算行星轮的径向变形以及应力。
图5所示为壁厚E=4.5 mm时的行星轮的应力云图,最大应力值达到550 MPa。图6为其径向变形云图,由仿真结果可知此时行星轮的径向最大变形量达到140 μm。

图4 有限元网格划分

图5 4壁厚4.5 mm行星轮应力

图6 壁厚4.5 mm行星轮径向变形量
假设行星轮壁厚为 2、2.5、3、3.5、4、4.5、5、5.5、6、6.5、7、7.5、8、8.5、9 mm,分别计算不同壁厚的中空弹性行星轮在4 712 N压紧力下的径向弹性变形量及对应的应力值。
图7为中空弹性行星轮取不同的壁厚时的径向弹性变形量和所受的最大应力。从图7可以看出:在4 712 N的压紧力作用下,弹性行星轮的径向变形随着壁厚的增加而逐渐减小,相应的最大应力也随着壁厚的增加而逐渐变小,与传统算法结果相基本一致。
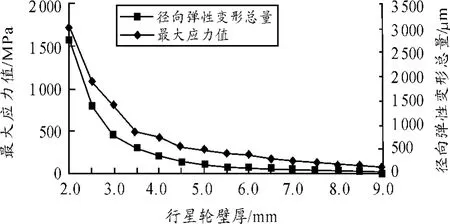
图7 行星轮的壁厚与径向变形量、最大应力关系曲线
由图7中数据可以看出,当壁厚小于4 mm时,行星轮的应力值偏大,大的应力容易使行星轮发生疲劳破坏。当壁厚大于5 mm时,行星轮的径向变形过小,不容易通过行星轮的弯曲变形来控制传动副之间的正压力;当壁厚为4.5 mm时,弹性行星轮比较符合设计的意图。所以弹性行星轮的壁厚取4.5 mm。
由以上分析计算得出壁厚为4.5 mm的弹性行星轮在装配状态径向变形量为140 μm时,弯曲变形提供的压紧力为4712 N。考虑到磨损的影响,为中空弹性行星轮预留5 μm的磨损量。
由以上分析计算可得,行星轮的最终设计尺寸为:Din=34.15 mm,Dout=25.14 mm,L=10 mm。
把最终设计方案建模并进行仿真分析得其应力云图,如图8所示。最大应力为610 MPa,压紧力为5 404 N,满足设计要求。
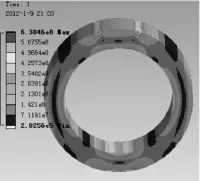
图8 行星轮静态应力云图
3 动态仿真验证
以上设计与仿真是装配状态下弹性行星轮的变形与应力,是对弹性行星轮的静态计算。在运转状态下,行星轮不仅受到径向的2个正压力,由于接触副之间存在牵引系数,行星轮还受到2个牵引力的作用。
行星轮在额定工况转速为16.75 rad/s,牵引副之间的牵引系数是0.1。将转速与牵引系数加载到行星轮进行动态仿真。图9为所设计行星轮动态应力云图,最大应力为660 MPa。

图9 行星轮动态应力云图
由行星轮的动态仿真结果可看出,行星轮最大应力有所增加,最大应力分布情况也有所不同,最大应力分布在行星轮内孔位置,但是其应力仍然在合理的范围之内。通过对中空弹性行星轮进行动态仿真,验证了本文设计的中空弹性行星轮是一种合理可靠的结构。
4 结论
1)行星牵引传动行星轮设计成空心是一种合理的结构,不仅可以利用行星轮的弯曲变形为传动机构提供合适的压紧力,而且中空行星轮的弯曲变形使得它与外圈、中心轮的接触面积增大,接触应力减小,有利于提高牵引副的接触寿命。
2)利用ANSYS Workbench建立行星轮模型,对其进行了静态分析,得到了行星轮壁厚与径向变形量的变化关系,并通过对行星轮运动状态的仿真,验证了行星轮的可靠性。
3)为预防行星轮长时间使用产生磨损造成压紧力不足,可以为弹性行星轮预留合理的磨损量,提高行星轮的使用寿命与安全系数。
[1]陈德生,潘荣荣.牵引传动研究综述[J].机械传动,2009,33(6):108 -110.
[2]许卫华.行星摩擦轮传动技术在电动自行车上的应用[J].电动车专辑,1998,27(9):340 -343.
[3]Donald R F,Qamhiyah A Z.A Self-Actuating Traction-Drive Speed Reducer[J].Journal of Mechanical Design,2005,42(4):857 -864.
[4]Marizan Mubin,Shigeto Ouehi,Masatoshi.Drive Control of an EIectric Vehicle by a Non-linear Controller[J].Journal of Materials Processing Technology,2006,6(3):300-308.
[5]周建军.行星牵引传动在冷却塔中的应用[J].机械传动,1996,20(3):42 -45.
[6]宣海军,吴荣仁.弹性圈高速行星牵引传动机构[J].机械传动,2002,26(1):50 -51.
[7]钱立新,陆君毅,吴荣仁,等.定速比牵引传动——高速传动的新选择[J].传动技术,1998,27(3):21 -25.
[8]Fang Zhengpeng,Miaosen Shen Holland.Application of Z-Source Inverter for Traction Drive of Fuel Cell-Battery Hybrid Electric Vehicles[J].Journal of aterials Processing Technology,2007,126(3):179 -187.
[9]龙振宇,姚顺培,汪海云,等.机械设计[M].北京:机械工业出版社,2001:119-123.
[10]徐灏,蔡春源,严隽琪,等.机械设计手册[K].北京:机械工业出版社,2001:343-346.
[11]顾志敏,张武高,黄震.车用甲醛燃料润滑性能的评定方法[J].上海交通大学学报,2008,42(1):142 -145.
[12]Ishibashi A.Planetary Traetion Drives with High Effieeneies.JSME International Confereneeon Motionand Power Transmission[J].Journal of Mechanical Design,1991,42(4):57 -64.
[13]钱立新,陆君毅,吴荣仁,等.高速牵引机构的中空滚子设计研究[J].机械传动,2003,21(3):5 -8.
[14]铁摩辛柯.材料力学[M].萧敬勋,译.天津:天津科学技术出版社,1989:115-151.
[15]陈会涛.往复牵引传动试验机的设计及初步研究[D].郑州:中原工学院,2008:7 -18.

